Logistic Regression的思考与整理

在NYU上了Machine Learning，学到了一些以前没有注意或者不知道的知识。在原有部分博文的基础上进行更详细地讲解。

关于回归算法的Bias和Variance

加深了对误差理论的理解。

对于一个输入为$\vec x$的回归算法，我们设算法输出的预测函数为$g(x)$，算法的真正分类函数为$f(x)$。我们期望的就是让$g(x)$尽可能地与$f(x)$靠近。

我们将$f(x)$和$g(x)$当成一个连续函数，那么对于特定的$x_i$，$r$表示输入数据在该点的值，且$f(x) = E[r|x_i]$（因为输入有噪声的缘故）。

$$\begin{aligned} E[(r-g(x_i))^2|x_i]\ =\ & \underbrace{E[(r-E[r|x_i])^2|x_i]}_{noise} - \underbrace{(E[r|x_i]-g(x_i))^2}_{square\ error = bias}\\ =\ & \underbrace{E[(r-f(x_i))^2|x_i]}_{noise} - \underbrace{(f(x_i)-g(x_i))^2}_{square\ error = bias} \end{aligned}$$

对于固定的$x_i$和一堆$g(x_i)$（我们可以认为是假设集里的所有函数），那么$g(x_i)$就变成了一个随机变量了。

现在考虑一个长度为$N$的$\vec{x}$随机样本，我们希望$g(x_i)$和$E[r|x_i]$是相同的。

$$\begin{aligned} E_{\vec x}[(E[r|x_i]-g(x_i))^2|x_i]\ =\ & \underbrace{(E[r|x_i]-E_{\vec x}[g(x_i)])^2}_{bias\ of\ learning\ alg\ on\ x_i}\\ & \underbrace{+E[(g(x_i)-E_{\vec x}[g(x_i)])^2]}_{variance\ of\ learning\ alg} \end{aligned}$$

其中后者指的是多个函数之间的variance。

例子1

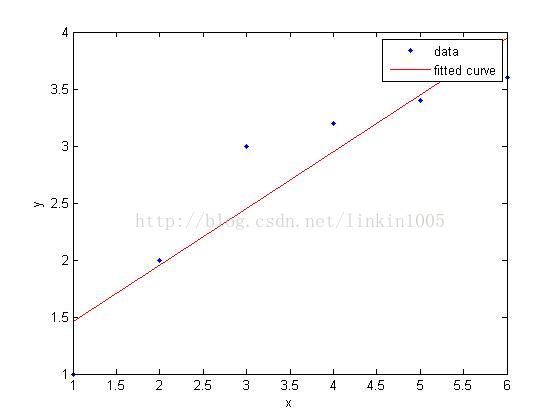
对于如图的输入样例，用一次函数去进行分类，那么我们可以明显地发现，对于特定的$x_i$，$g(x_i)$造成的bias非常大，也就是square error特别大。

但是考虑到假设集合（即，所有一次函数的集合），多个$g(x)$之间的variance是较小的。反正一次函数变来变去就只有ABC三个参数变，化简一下就只剩下斜率和偏移能够变化了。

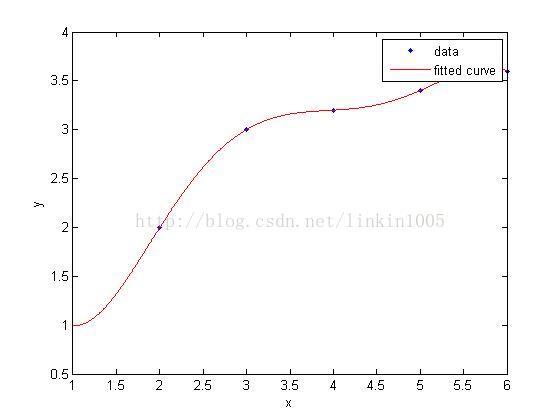
那么当我们用五次函数去训练分类的时候，我们可以明显地发现，对于特定的$x_i$，$g(x_i)$造成的bias为0，但是五次函数的variance就明显比一次函数大多了。

所以图1是欠拟合，图2则是过拟合。

例子2

设$f(x)=2$，在输入的时候没有噪音，即$r = f(x) = 2$。

设计算法：

1. 当第一个输入的样例$(x^\prime, r^\prime)$中$x^\prime > 10$，则让$g(x)=1$。
2. 否则。让$g(x)=3$

对于训练集合，我们让$x^t$均匀得从$[0,20]$中随机得出。

设

$${\vec x}=\{(4,2), (5,2), (7,2)\}$$

我们可以看得出来这题的算法得出的$g(x)$的variance为0，但是它的bias却非常大。

关于逻辑回归函数的由来

Logistic函数

看到一个博客上面说逻辑回归为啥叫逻辑回归，是因为它用了Logistic函数。当时我就觉得非常牛逼，这个函数是科学家用硬生生猜出来的么。

现在才知道这个函数也是推导出来的。

我们要预测一个样本$x$的类别，则需要比较一下在输入为的x条件下，两个类别的概率大小

$$P[+|x] = y\\P[-|x] = 1-y$$

我们假设可以假设$P[+|x]>P[-|x]$。

$$y > 1-y\Rightarrow {y\over 1-y}>1\Rightarrow log[{y\over 1-y}]>0$$

那么我们就考虑函数$f(x) = log({y\over 1-y})$。

我们让$z = log({y\over 1-y})\Rightarrow y = {1\over 1+e^{-z}}$，

同时我们让$w_dx_d+\dots+w_1x_1+w_0=z$，可以得到

$$P[+|x]={1\over 1+e^{-w^Tx+w_0}}$$

这就是Logistic函数的由来。

损失函数的由来

逻辑回归的损失函数是由log对数损失函数得来的。

输入$x_1,x_2,x_3$，那么他们的分类是$1,1,0$的概率是

$$P[1|x_1]\times P[1|x_2]\times P[0|x_3]\\\Rightarrow logP[1|x_1]+logP[1|x_2]+logP[0|x_3]$$

我们让$y=P[1|x]$，那么对于$x_1,\dots,x_n$得到分类结果是$r^1,\dots,r^n$的概率是

$$\prod_{t=1}^n(y^t)^{r^t}(1-y^t)^{1-r^t}\\ \Rightarrow \sum_{t=1}^n(log((y^t)^{r^t}(1-y^t)^{1-r^t}))\\ = \sum_{t=1}^n[r^tlog(y^t)+(1-r^t)log(1-y^t)] \rightarrow cross\ entropy$$

最后得出的就是交叉熵

而我们的期望是找到$\vec w$来使交叉熵最大，这样等价于找到一个$\vec w$使得交叉熵的相反数最小。

我们可以假设$olog0=0$。

1. 当$r^t=1$时，$cost = -log(y^t)$
2. 当$r^t=0$时，$cost = -log(1-y^t)$

将以上两个表达式合并为一个，则单个样本的损失函数可以描述为：

$$cost(x,y)=−r^tlog(y^t)−(1−r^t)log(1−y^t)$$

全体样本的损失函数可以表示为：

$$\begin{aligned} cost({\vec r}, {\vec y}) = & \sum_{t=1}^n[r^tlog(y^t)+(1-r^t)log(1-y^t)] \end{aligned}$$

这就是逻辑回归最终的损失函数表达式。

大家可以将$y=P[1|x]={1\over 1+e^{-w^Tx+w_0}}$带入后进行求导，则可以得到

$${\partial E\over \partial w_j}=\sum_{t=1}^nr^tx^t-\sum_{t=1}^n{(1-{1\over 1+e^{-w^Tx+w_0}})x^t}$$

大家可以发现，使得上面的导数为0，是无法求出解的，所以只能用梯度下降计算

$$z = sigmoid(a)\\ \Rightarrow {d z\over d a} = z(1-z)\\ \Rightarrow {\partial\over \partial w_j} = -(r^t-y^t)\sum X_j^t$$

如果再考虑learning rate就可以了。