关于Elastic Net、Lasso Regression、Ridge Regression的3个解释引用

最新推荐文章于 2024-03-16 18:26:11 发布

默一鸣

最新推荐文章于 2024-03-16 18:26:11 发布

阅读量7.9k

点赞数 2

分类专栏： ML 文章标签： lasso Elastic Ridge Regression

本文链接：https://blog.csdn.net/yimingsilence/article/details/79390859

版权

ML 专栏收录该内容

82 篇文章 4 订阅

订阅专栏

关于这个问题，从不同的切入点，出发点，都有比较不同的深入的解释，但是这些都是等价的。

找了4个比较好的解释

一、

作者：杨军
链接：https://www.zhihu.com/question/38121173/answer/85813729
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

线性回归问题是很经典的机器学习问题了。

适用的方法也蛮多，有标准的Ordinary Least Squares，还有带了L2正则的Ridge Regression以及L1正则的Lasso Regression。

这些不同的回归模型的差异和设计动机是什么？

在本帖的一个高票回答[1]里，把这个问题讨论得其实已经相当清楚了。

我在这里的回答更多是一个知识性的总结，在Scott Young的《如何高效学习》[6]里提到高效学习的几个环节：获取、理解、拓展、纠错、应用、测试。
在我来看，用自己的语言对来整理对一个问题的认识，就是理解和扩展的一种形式，而发在这里也算是一种应用、测试兼顾纠错的形式了。

首先来看什么是回归问题，直白来说，就是给定
$\vec X \in \mathcal R_D (1.1)$
$Y \in \mathcal R (1.2)$
$Y=\boldsymbol f(\vec X) (1.3)$
其中映射函数 $\boldsymbol f$ 未知，但是我们手上有一堆数据样本 $\mathcal T$ ，形式如下：
$(\vec X_1, Y_1), (\vec X_2, Y_2), ... (\vec X_n, Y_n) (2.1)$
我们期望从数据样本里推断出映射函数 $\boldsymbol f$ ，满足
$argmin_fE(f(\vec X_i) - Y_i)^2 (3.1)$
即期望推断出的映射函数在数据样本上与真实目标的期望差异尽可能最小化。

通常来说，数据样本中每个样本的出现频率都可以认为是1，而我们要推断的映射函数可以认为是
一个线性函数
$f(\vec X)=w_1X_1 + w_2X_2 + ... + w_nX_n + \beta(4.1)$
其中 $w_1, w_2, ... w_n, \beta (4.2)$ 就是我们要推断的关键参数了。
这样的问题就是线性回归(Linear Regression)问题。

Ordinary Linear Square的求解方法很直白，结合上面的描述，我们可以将 $argmin_fE(f(\vec X) - Y)^2 (5.1)$
具像化为求解函数
$\sum_{i=1}^{N}(f(\vec X_i) - Y_i)^2 (5.2)$
的最小值以及对应的关键参数。

对于这个目标函数，我们可以通过求导计算[2]，直接得出解析解如下： $\vec w = (X_TX)^{-1}X^T\vec Y(5.3)$

当然，这是一个典型的Convex优化问题，也可以通过迭代求优的算法来进行求解，比如Gradient Descent或者Newton法[2]。

看起来不错，那么为什么我们还要在OLS的基础上提供了Ridge Regression(L2正则)和Lasso Regression(L1正则)呢?

如果说得笼统一些的话，是为了避免over-fit，如果再深入一些，则可以这样来理解：
不引入正则项的OLS的解很可能会不stable，具体来说，两次不同的采样所采集到的训练数据，用于训练同一个线性回归模型，训练数据的些微差异，最终学出的模型差异可能是巨大的。在[3]里有一个例子：

还是在[3]里，提供了一个定量的证明：

结果的证明细节，有兴趣的同学可以自己去查阅，这里直接把关键点引用如下：

一个有名的病态矩阵是Hilbert矩阵[4]，其形如下：

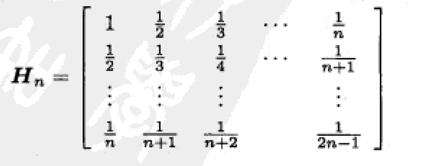
再回到我们关于OLS的讨论，我们不难看出，随着训练样本采样次数的增加，采样到病态阵的概率会增多，这样一来学出的模型的稳定性就比较
差。想象一下，今天训练出来的模型跟明天训练出的模型，存在明显的模型权值差异，这看起来并不是一件非常好的事情。

那么病态阵的根本原因是什么呢？条件数的描述还是相对有些抽象，所以这里又引入了奇异阵的概念。

什么是奇异阵呢？
形式化来说，不存在逆矩阵的方阵（因为OLS的闭式解里，需要求逆的矩阵是 $X^TX(6.1)$
一定是一个方阵，所以这里仅讨论方阵这一特殊形态）就是奇异阵，即 $A^{-1}A=\mathcal I, \not \exists A^{-1}(6.2)$
那么再具体一些，什么样的方阵会不存在逆呢？
非满秩、矩阵的特征值之和为0、矩阵的行列式为0。
满足这三个条件中的任意一个条件，即可推出方阵为奇异阵，不可求逆，实际上这三个条件是可以互相推导出来的。
而我们又知道，一个方阵的逆矩阵可以通过其伴随矩阵和行列式求出来[7]
$A^{-1}=\frac {1} {|A|} adj(A); adj(A) \in R^{n*n}, (adj(A))_{ij}=(-1)^{i+j}|A_{\setminus j,\setminus i}|(6.3)$

从这里，其实可以看的出来，对于近似奇异阵，其行列式非常接近于0，所以
$\frac 1 {|A|} (6.4)$
会是一个非常大的数，这其实反映出来就是在计算A的逆矩阵时，伴随矩阵上的些微变化，会被很大程度上放大，就会导致多次采样出来的训练数据，学出的模型差异很大，这是除了上面提到的条件数以外的另一种比较形象的解释了。
如果类比普通代数的话，奇异阵就好比是0，0不存在倒数，越接近0的数，其倒数越大，同样，奇异阵不存在逆矩阵，而接近奇异阵的逆矩阵的波动也会比较大。
所以跟奇异阵有多像(数学语言里称为near singularity)，决定了我们的线性回归模型有多么不稳定。
既然知道了奇异阵的性质并且了解到是奇异阵使得从训练数据中学出来的线性回归模型不那么稳定，那么我们是不是可以人为地通过引入一些transformation让 $X^TX(7.1)$ 长得跟奇异阵不那么像呢？
我们知道
$|A|=\Pi_i^n \lambda_i(7.2)$
$trA=\sum_{i=1}{n}\lambda_i(7.3)$
$trA=\sum_{i=1}^nA_{ii}(7.4)$
于是一个直观的思路是在方阵 $X^TX$ 的对角线元素上施加如下的线性变换
$X^TX+\lambda\mathcal I (7.5)$
其中 $\mathcal I$ 是单位阵。
有了上面的变换以后，对角线的元素为全零的概率就可以有效降低，也就达到了减少 $X^TX$
near singularity的程度，进而减少线性回归模型不稳定性的目的了。
那么这个变换跟Ridge或是Lasso有什么关系呢？
实际上， $\vec w=(X^TX+\lambda \mathcal I)^{-1}X\vec Y(7.6)$ (7.6)正是对下面的 $\sum_{i=1}^{N}(\vec w\vec X_i - Y_i)^2 + \lambda ||\vec w||_2^2(7.7)$
这个优化问题为 $\vec w$ 计算闭式解得到的结果(在[2]里OLS的闭式解的推导过程里加入二范数正则项，蛮自然地就会得到7.6里的结果，[8]里也有类似的推论)。
而(7.7)正是Ridge Regression的标准写法。
进一步，Lasso Regression的写法是 $\sum_{i=1}^{N}(\vec w\vec X_i - Y_i)^2 + \lambda ||\vec w||_1$
这实际上也是在原始矩阵上施加了一些变换，期望离奇异阵远一些，另外1范数的引入，使得模型训练的过程本身包含了model selection的功能，在上面的回复里都举出了很多的例子，在一本像样些的ML/DM的教材里也大抵都有着比形象的示例图，在这里我就不再重复了。
一个略微想提一下的是，对于2范数，本质上其实是对误差的高斯先验，而1范数则对应于误差的Laplace先验，这算是另一个理解正则化的视角了。
只不过1范数的引入导致优化目标不再处处连续不能直接求取闭式解，而不得不resort到迭代求优的方法上了，而因为其非处处连续的特点，即便是在迭代求优的过程中，也变得有些特殊了，这个我们可以在以后讨论OWLQN和LBFGS算法的时后再详细引出来。

[1]. Linear least squares, Lasso,ridge regression有何本质区别？ - 数据挖掘
[2]. http://cs229.stanford.edu/notes/cs229-notes1.pdf
[3]. 《数值分析导论》( 数值分析导论 (豆瓣) )的例6.5.3
[4]. 《数值分析导论》( 数值分析导论 (豆瓣) )的例6.5.5
[5]. 关于奇异阵的资料。
[6]. 如何高效学习 (豆瓣) 如何高效学习 (豆瓣)
[7]. http://cs229.stanford.edu/section/cs229-linalg.pdf
[8]. PRML 3.28

二、

作者：高大花
链接：https://www.zhihu.com/question/38121173/answer/75198908
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

题主这个问题算是比较基础的，那我回答也详细点好了。个人理解，不当之初欢迎各位大牛指正。
知乎公式编辑器导致意外换行问题不知如何解决……各位看官帮帮忙。

1. Least-squares（最小二乘法）是最经典的机器学习算法，后续的大部分机器学习算法（包括题主提到的Lasso,ridge regression）都是在其基础上发展而来的。Linear model即 $f _{\theta}(x)=\sum_{j=1}^{b}{\theta _{j}\phi _{j}(x)}$ ，只要求得其参数 $\left\{ \theta \right\} _{j=1}^{b}$ ，便可以得到自变量 $x$ 与因变量 $y$ 的映射关系。因此有监督回归的任务就是通过 $n$ 个成对的训练样本 $\left\{ (x_{i}, y_{i} )\right\} _{i=1}^{n}$ 来求得学习模型的参数 $\left\{ \theta \right\} _{j=1}^{b}$ 。

2. 最小二乘法是对模型的输出 $f _{\theta}(x_{i} )$ 和训练样本的输出 $\left\{y_{i} \right\} _{i=1}^{n}$ 的平方误差 $\sum_{i=1}^{n}{\left( f _{\theta}(x_{i} )-y_{i} \right) } ^{2}$ 为最小时的参数 $\theta _{LS}$ 进行学习。 $\sum_{i=1}^{n}{\left( f _{\theta}(x_{i} )-y_{i} \right) } ^{2}$ 称之为损失函数。随着学习模型 $f _{\theta}(x)$ 复杂度的提高，这种经典最小二乘法存在的诸多缺陷也表露出来，其中一个重要的问题就是对训练数据的过拟合（overfitting）。过拟合的原因被认为是学习模型相比真实模型过于复杂。因此为解决过拟合问题，可在损失函数的后面加上一个约束条件从而限制模型的复杂度，这个约束条件即为正则化项（regularizer）。典型的正则化方法就是引入 $l_{2}$ 约束， $l_{2}$ 约束的约束条件是参数的 $\left\{ \theta \right\} _{j=1}^{b}$ 的 $l_{2}$ 范数小于某个阈值，此时最小二乘学习法的学习目标变为使学习结果的平方误差与正则化项的和最小。虽然这种方法对于预防过拟合非常有效，但当学习模型中的参数特别多时，求解各参数需要花费大量的时间。因此，一种能够把大部分参数都设置为0的学习方法便被提出，就是稀疏学习，Lasso回归就是典型的稀疏学习。

3. Lasso回归的本质是 $l_{1}$ 约束的最小二乘法，即学习模型参数 $\left\{ \theta \right\} _{j=1}^{b}$ 的 $l_{1}$ 范数小于某个阈值。想象一下， $l_{2}$ 约束下的参数分布趋向于以圆点为中心的圆周内部，而 $l_{1}$ 约束下的参数则集中分布在各坐标轴附近，因此 $l_{1}$ 约束能够有效的将若干参数的解收敛到0。约束的求解相对于 $l_{2}$ 约束更为复杂，通常解法是需要数个 $l_{2}$ 约束求解的迭代过程。因此，题主所问的 $l_{1}$ 和 $l_{2}$ 约束如何选取的问题，个人认为如果不考虑 $l_{1} +l_{2}$ 约束的弹性网回归， $l_{1}$ 约束更适合参数较多或需要特征提取的情况下， $l_{2}$ 约束更适合模型简单或是不想求解那么复杂的情况下（MATLAB算这两种约束都很简单）。

4. 岭回归也是最小二乘法正则化方法的一种延伸，特点是以损失无偏性为代价换取数值稳定性。

希望能帮到你。

三、

L1正则化使得模型更加稀疏，L2使得模型参数更趋近于0，提高泛化能力(这里是另外一个解释:https://www.zhihu.com/question/38081976/answer/74895039)

先介绍下各自的用处：

L0范数：就是指矩阵中非零元素的个数，很显然，在损失函数后面加上L0正则项就能够得到稀疏解，但是L0范数很难求解，是一个NP问题，因此转为求解相对容易的L1范数（l1能够实现稀疏性是因为l1是L0范数的最优凸近似）
这里写图片描述

L1范数：矩阵中所有元素的绝对值的和。损失函数后面加上L1正则项就成了著名的Lasso问题（Least Absolute Shrinkage and Selection Operator），L1范数可以约束方程的稀疏性，该稀疏性可应用于特征选择：
比如，有一个分类问题，其中一个类别Yi(i=0,1),特征向量为Xj（j=0,1~~~1000），那么构造一个方程
Yi = W0*X0+W1*X1···Wj*Xj···W1000*X1000+b;
其中W为权重系数，那么通过L1范数约束求解，得到的W系数是稀疏的，那么对应的X值可能就是比较重要的，这样就达到了特征选择的目的（该例子是自己思考后得出的，不知道正不正确，欢迎指正）。

L2范数：
其实就是矩阵所有元素的平方和开根号，即欧式距离，在回归问题中，在损失函数（或代价函数）后面加上L2正则项就变成了岭回归（Ridge Regression），也有人叫他权重衰减，L2正则项的一个很大的用处就是用于防止机器学习中的过拟合问题，同L1范数一样，L2范数也可以对方程的解进行约束，但他的约束相对L1更平滑，在模型预测中，L2往往比L1好。L2会让W的每个元素都很小，接近于0，但是不会等于0.而越小的参数模型越简单，越不容易产生过拟合，以下引自另一篇文章：
到目前为止，我们只是解释了L2正则化项有让w“变小”的效果（公式中的lamda越大，最后求得的w越小），但是还没解释为什么w“变小”可以防止overfitting？一个所谓“显而易见”的解释就是：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。当然，对于很多人（包括我）来说，这个解释似乎不那么显而易见，所以这里添加一个稍微数学一点的解释：

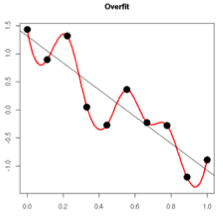
过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。
这里写图片描述

而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

弹性网络（Elastic Net）：实际上是L1，L2的综合

这里写图片描述

其中的L1正则项产生稀疏模型
L2正则项产生以下几个作用：
1 消除L1正则项中选择变量个数的限制（即稀疏性）
2 产生grouping effect（对于一组相关性较强的原子，L1会在相关的变量间***随机***的选择一个来实现稀疏）
3 稳定L1正则项的路径
整理后的正则项：

这里写图片描述

e lastic net 的几何结构：

这里写图片描述

其结构有如下两个特点：
1 在顶点具有奇异性（稀疏性的必要条件）
2 严格的凸边缘（凸效应的强度随着α而变化（产生grouping效应））

elastic net总结：
1 弹性网络同时进行正则化与变量选择
2 能够进行grouped selection
3 当p>>n，或者严重的多重共线性情况时，效果明显
4 当α接近0时，elastic net表现接近lasso，但去掉了由极端相关引起的退化或者奇怪的表现
5 当α从1变化到0时，目标函数的稀疏解（系数为0的情况）从0增加到lasso的稀疏解

L1 L2区别总结:
加入正则项是为了避免过拟合,或解进行某种约束,需要解保持某种特性
L1正则假设参数的先验分布是Laplace分布，可以保证模型的稀疏性，也就是某些参数等于0,L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果,
L1也称Lasso；

L2正则假设参数的先验分布是Gaussian分布，可以保证模型的稳定性，也就是参数的值不会太大或太小.L2范数是各参数的平方和再求平方根，我们让L2范数的正则项最小，可以使W的每个元素都很小，都接近于0。但与L1范数不一样的是，它不会是每个元素为0，而只是接近于0。越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。

L2正则化江湖人称Ridge，也称“岭回归”

在实际使用中，如果特征是高维稀疏的，则使用L1正则；如果特征是低维稠密的，则使用L2正则。

L2不能控制feature的“个数”，但是能防止模型overfit到某个feature上；相反L1是控制feature“个数”的，并且鼓励模型在少量几个feature上有较大的权重。

四

Elstic Net 模型家族理论简介

在这一节我们会了解一些关于 Elastic Net 模型家族的理论。首先我们先来看看一般线性 Elastic Net 模型的目标函数：

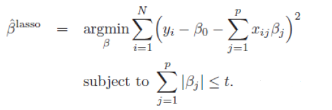
目标函数的第一行与传统线性回归模型完全相同，即我们希望得到相应的自变量系数 $β$ ，以此最小化实际因变量 y 与预测应变量 $β x$ 之间的误差平方和。而线性 Elastic Net 与线性回归的不同之处就在于有无第二行的这个约束，线性 Elastic Net 希望得到的自变量系数是在由 $t$ 控制的一个范围内。这一约束也是 Elastic Net 模型能进行复杂度调整，LASSO 回归能进行变量筛选和复杂度调整的原因。我们可以通过下面的这张图来解释这个道理：

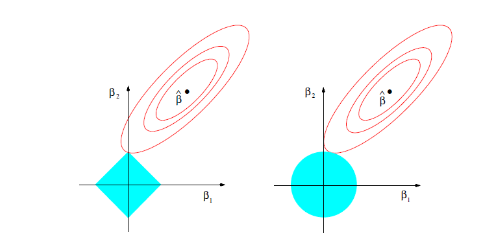
先看左图，假设一个二维模型对应的系数是 $β_{1}$ 和 $β_{2}$ ，然后 $^β$ 是最小化误差平方和的点，即用传统线性回归得到的自变量系数。但我们想让这个系数点必须落在蓝色的正方形内，所以就有了一系列围绕 $^β$ 的同心椭圆，其中最先与蓝色正方形接触的点，就是符合约束同时最小化误差平方和的点。这个点就是同一个问题 LASSO 回归得到的自变量系数。因为约束是一个正方形，所以除非相切，正方形与同心椭圆的接触点往往在正方形顶点上。而顶点又落在坐标轴上，这就意味着符合约束的自变量系数有一个值是 0。所以这里传统线性回归得到的是 $β_{1}$ 和 $β_{2}$ 都起作用的模型，而 LASSO 回归得到的是只有 $β_{2}$ 有作用的模型，这就是 LASSO 回归能筛选变量的原因。

而正方形的大小就决定了复杂度调整的程度。假设这个正方形极小，近似于一个点，那么 LASSO 回归得到的就是一个只有常量（intercept）而其他自变量系数都为 0 的模型，这是模型简化的极端情况。由此我们可以明白，控制复杂度调整程度的 λ 值与约束大小 $t$ 是呈反比的，即 λ 值越大对参数较多的线性模型的惩罚力度就越大，越容易得到一个简单的模型。

另外，我们之前提到的参数 α 就决定了这个约束的形状。刚才提到 LASSO 回归（α=1）的约束是一个正方形，所以更容易让约束后的系数点落在顶点上，从而起到变量筛选或者说降维的目的。而 Ridge 回归（α=0）的约束是一个圆，与同心椭圆的相切点会在圆上的任何位置，所以 Ridge 回归并没有变量筛选的功能。相应的，当几个自变量高度相关时，LASSO 回归会倾向于选出其中的任意一个加入到筛选后的模型中，而 Ridge 回归则会把这一组自变量都挑选出来。至于一般的 Elastic Net 模型（0<α<1），其约束的形状介于正方形与圆形之间，所以其特点就是在任意选出一个自变量或者一组自变量之间权衡。

下面我们就通过 Logistic 回归一节的例子，来看看这几种模型会得到怎样不同的结果：

# CV for 11 alpha value
for (i in 0:10) {
  assign(paste("cvfit", i, sep=""),
  cv.glmnet(x, y, family="binomial", type.measure="class", alpha=i/10))
}
# Plot Solution Paths
par(mfrow=c(3,1))
plot(cvfit10, main="LASSO")
plot(cvfit0, main="Ridge")
plot(cvfit5, main="Elastic Net")

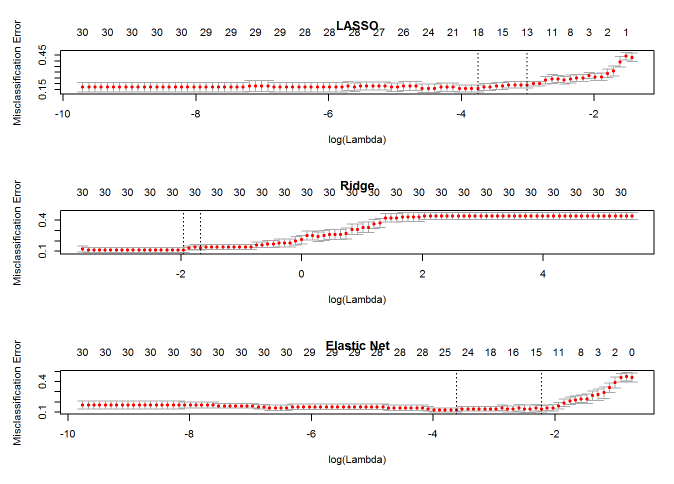
通过比较可以看出，Ridge 回归得到的模型一直都有 30 个自变量，而 α=0.5 时的 Elastic Net 与 LASSO 回归有相似的性能。

默一鸣

关注

2
点赞
踩
13

收藏

觉得还不错? 一键收藏
0
评论
关于Elastic Net、Lasso Regression、Ridge Regression的3个解释引用

关于这个问题，从不同的切入点，出发点，都有比较不同的深入的解释，但是这些都是等价的。找了4个比较好的解释一、作者：杨军链接：https://www.zhihu.com/question/38121173/answer/85813729来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。线性回归问题是很经典的机器学习问题了。适用的方法也蛮多，有标准的Ordinary Lea...
复制链接

扫一扫