2.3.3 Bayes'theorem for Gaussian variables
之前两节,书中用标准二次型和配方的方法找到了p(xa)和p(xb|xa),这一节中,把它们记为p(x)和p(y|x),并把他们当作贝叶斯理论中的先验概率和似然函数,用以求得p(y)和后验概率p(x|y)。为了简化描述,作者先对之前的结论进行了描述的简化,定义了三个新的参数(对照上一节可知三个参数的含义),并随之引出了线性高斯模型的概念。
一如之前分块的方法,这次书中将x,y拼接:
即,p(x,y)=p(z)。然后作者通过最上面的两个公式,利用x和y|x分布的期望和协方差矩阵进行推导,得到关于z的二次型。这样便得到了z的协方差矩阵,不同的是,现在z的协方差矩阵已经被x和y|x的参数所表示,再通过配方法得到z的均值,这样便可以得到p(y)的期望和协方差矩阵了。关于p(x|y),我们已经有p(x)p(y|x)和p(y),利用公式p(x)p(y|x)/p(y),不难得出后验概率。
2.3.4 Maximum likelihood for Gaussian
假设X服从多维高斯正态分布,可以得到密度函数的log形式,对log函数中的μ球偏导(求导过程利用了附录C的公式19),并令偏导数为“0”,可以得到μ的最大似然估计:
关于样本协方差矩阵的最大似然估计是怎么得到的,作者似乎并没有特别明确说明,直接给出了结果。如同单维高斯分布一样,作者又提出了样本均值是期望的无偏估计,而样本协方差矩阵则是协方差矩阵的有偏估计,从而引起过拟合。所以对估计量进行修正:
2.3.5 Sequential estimation
利用上一小节得到的μ的最大似然估计








 本文是PRML书籍的阅读笔记,涵盖了贝叶斯定理在高斯变量上的应用,最大似然估计,序贯估计的Robbins-Monro算法,以及高斯分布的贝叶斯推断。此外,还讨论了Student's t分布的健壮性和周期性变量的建模,如von Mises分布。最后,引入了高斯混合模型的概念。
本文是PRML书籍的阅读笔记,涵盖了贝叶斯定理在高斯变量上的应用,最大似然估计,序贯估计的Robbins-Monro算法,以及高斯分布的贝叶斯推断。此外,还讨论了Student's t分布的健壮性和周期性变量的建模,如von Mises分布。最后,引入了高斯混合模型的概念。
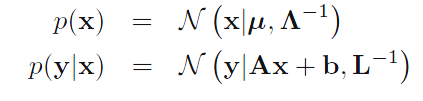
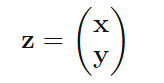
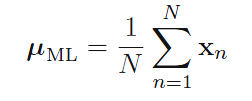
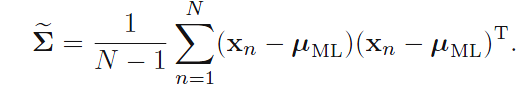
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1711
1711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








