简单回顾一下,在直角坐标系里,水平的叫x轴,竖直的叫y轴,两轴交点叫原点。我们描述一个点,会用它到两轴的距离x、y来表示①。

极坐标系②呢,只有一条射线,左端点叫极点,这条射线叫极轴。描述点的时候,会用这个点到极点的距离ρ,以及该点和极点的连线l,与极轴的夹角θ来表示。

虽然你现在不喜欢极坐标系,但是你不了解一个人的时候,也很难特别喜欢他。
今天先拿直线来说,你可能不喜欢,但要熬过认识它的第一阶段。
从最简单的开始:
01


如果我们把它放在原点,那你会说它的斜率是

这条直线的方程就是y=x。
发现没有,你习惯性的表示x和y之间的关系,从而得到直线方程。
那如果把它放在极坐标系里呢,一样的思路,去找ρ和θ的关系就好。

这条直线上所有的点,到极轴的夹角都是

而这些点到极点的距离是任意的,所以直线方程就是

,吗?

觉不觉的有问题?我们随便取点验证一下。



所以其实,这条直线的方程的是由两条射线构成的,完整写出来就是:

我们发现,随便取点,是一个非常重要的方法!
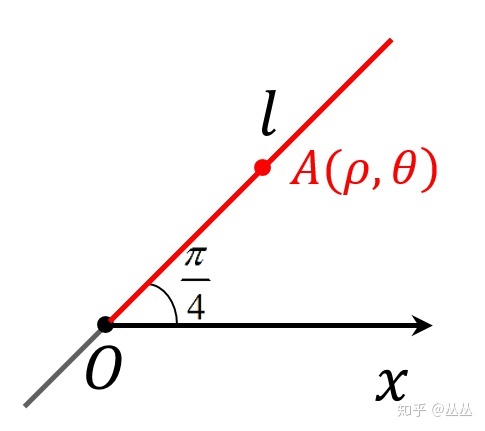
用“在直线上任取点A(ρ,θ),观察图形,找ρ和θ的关系”这种方法,我们试试其他直线的方程怎么写:
02
一条过点P(2,0),且垂直于极轴的直线方程?

在直线l上任取一点A(ρ,θ),在图上找到A点的极径ρ和极角θ。

从直角△OPA里面可以发现:

,
这就是ρ和θ的关系,简单整理一下就好了:

所以构造直角三角形,是找几何关系的重要方法。同类型的特殊直线,还有平行于坐标轴的,你试一下:
03


在直线l上任取一点A(ρ,θ),在图上找到A点的极径ρ和极角θ。

构造直角三角形,找ρ和θ的关系:


整理一下:
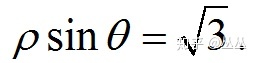
好,说了这么多特殊情况,一条长相随意的直线方程呢?
04
设直线l过点P(r,α),与极轴的夹角为β,求直线l的极坐标方程。

题目的图


标上几何量的图


找到任意点A(ρ,θ)的图

这次没有直角三角形了,三角形里还有哪些边角关系?——正弦定理!

找到ρ和θ的关系的图

在△OPA中,由正弦定理得:

05
其实,如果你愿意抛开自己的求知欲去看前面的几个问题,你也可以把它们全都转化成直角坐标系里的问题来解,再用公式④转化成极坐标方程:



2.一条过点P(2,0),且垂直于极轴的直线方程?



4.设直线l过点P(r,α),与极轴的夹角为β,求直线l的极坐标方程。


ps
①直角坐标系里,坐标有正负你知道的,我喜欢把符号理解成方向。
②关于极坐标系的概念,在这篇推文里:极坐标系。
③有的时候,为了表示方便,也可以像直角坐标系里那样,给ρ加上符号表示方向,这样的话ρ∈R就行了,直线写成:
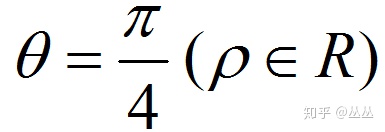
.
④详情推荐两篇推文:直角坐标与极坐标的转化,直角坐标方程与极坐标方程的转化。








 本文介绍了如何在极坐标系中表示直线,通过举例说明不同类型的直线方程,包括与极轴平行、垂直的直线,以及一般直线的极坐标形式。利用直角三角形的几何关系和正弦定理推导出极坐标方程,并强调了在直线上任取点进行验证的重要性。
本文介绍了如何在极坐标系中表示直线,通过举例说明不同类型的直线方程,包括与极轴平行、垂直的直线,以及一般直线的极坐标形式。利用直角三角形的几何关系和正弦定理推导出极坐标方程,并强调了在直线上任取点进行验证的重要性。
















 2908
2908

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








