点到多边形的切线

前言

切线的构造属于计算几何中的基础问题。存在高效的算法可以计算凸集的切线。对于凹集，其切线与对应凸集的切线相同，所以也能高效计算。因此，我们这里仅仅讨论凸多边形的切线。

寻找切线的算法与寻找极值点的算法（凸多边形的极值点）类似。通过运用相似的二分搜索方法，我们能构造O(logn)复杂度的切线寻找算法。

定义

直线L与多边形S相切定义为：L与S接触，但不穿过S的边界。也就是L仅仅与S的一个点相交或者与一条边重合。

根据上面的定义，S中的所有点要么在L上，要么都在L的同一侧。从外部任意一点，存在两条切线与S相切。

不妨设,以逆时针方向给出。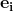为第i条边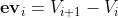，为边向量，由Vi指向Vi+1。想象一下，站在Vi点面朝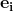的方向，如果P点在左手边，那么称P点在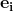左侧。

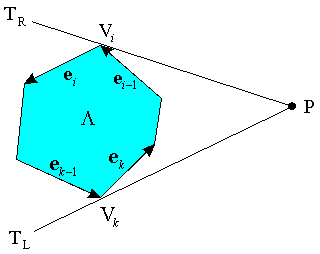
如上图所示。记P点为多边形S外部任意一点。对于任意一个顶点Vi，可以用下面的方法很方便地检查直线PVi是否是切线：

考虑Vi前后的两条边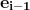和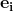。如果点P在这两条边的同一侧（同在左侧或者同在右侧），那么Vi-1和Vi+1一定在直线PVi的不同侧，PVi就一定不是切线。反之，若点P在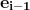的左侧，而在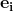的右侧，或者相反，那么点P就是一条切线。如上图，点P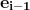在右侧而在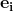左侧，那么点P是最右切线；同样地，点P在