1.
%用克莱姆法则求解方程组
clear
n=input('方程个数=')
A=input('系数矩阵A=')
b=input('常数列向量b=')
if((size(A)~=[n,n])|(size(b)~=[n,1])) %判断矩阵A和向量b输入格式是否正确
disp('输入不正确,要求A是n阶方阵,b是n维列向量') %disp:显示字符串
elseif det(A)==0 %判断系数行列式是否为零
disp('系数行列式为零,不能用克莱姆法则解此方程。')
else
for i=1:n %计算x1,x2,...xn
B=A;
B(:,i)=b;
x(i)=det(B)/det(A);
end
x=x' %以列向量形式显示方程组的解
end2.
%逆矩阵各种求法:
clear
A=[-7 -2 -6 4 6;1 3 -6 3 11;3 -11 9 5 -2;-3 0 -2 9 -3;7 30 -18 11 4]
%1.命令法:
An1=inv(A)
%2.幂运算法:
An2=A^-1
%3.右除法:
An3=eye(5)/A
%4.左除法
An4=A\eye(5)
%5.初等行变换法:
B=rref([A,eye(5)]); %对矩阵[A,I]进行初等行变换,B为矩阵A的最简行阶梯矩阵
if (rank(B(:,1:5))==5) %判断最简行阶梯矩阵B的前5列是否为单位阵
An5=B(:,6:10)
else
disp('A不可逆');
end
%6. 伴随矩阵求逆法:
for i =1:5
for j=1:5
T=A;
T(i,:)=[]; %删去矩阵T的第i行
T(:,j)=[]; %删去矩阵T的第j列
AA(j,i)=(-1)^(i+j)*det(T);
end
end
if det(A)~=0
An6=AA/det(A)
else
disp('A不可逆');
end
%求解符号行列式方程
clear
syms x %定义x为符号变量
A=[3,2,1,1;3,2,2-x^2,1;5,1,3,2;7-x^2,1,3,2]
D=det(A) %计算含符号变量矩阵A的行列式D
f=factor(D) %对行列式D进行因式分解
X=solve(D)
%验证行列式按行展开公式
clear
format long
A=round(randn(5)*10) %构造一个5阶随机数方阵A
s=0;
for j=1:5 %按第一行展开
T=A;
T(1,:)=[];
T(:,j)=[];
s=s+A(1,j)*(-1)^(1+j)*det(T);
end
s
D=det(A)











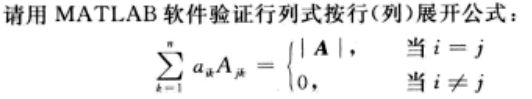
















 631
631

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








