前言
1.1、(显微镜)发展历史
1.2、(显微镜)光学元件
物镜 —— 由若干个透镜组成的一个复合透镜
- 主要功能:放大图像
- 其他功能:提高分辨率、改变焦距和聚焦、收集光信号
一、(相机)分辨率的影响因素:像元尺寸 + 信噪比
(相机)分辨率由像元尺寸和信噪比相互制约。
- (1)若相机的像元尺寸越小,则单位距离内的像素越多,分辨率越高。
- (2)若相机的像元尺寸越大,则落到一个像素上的光子就越多,信噪比越高。
1.1、(相机)分辨率的数学概念
若相机的像元尺寸不变,则像素越多,分辨率越高。
像素:是数字图像的最小单元。分辨率:在每个方向上的像素个数。
1.1.1、显示屏分辨率
每英寸像素(Pixels Per Inch, PPI), 又称为屏幕像素密度。即每英寸上的像素个数。
##############################################################
显示屏尺寸:显示器屏幕对角线的长度,单位英寸(1英寸 = 25.4毫米)
举例:
已知:主屏尺寸 = 4英寸,主屏分辨率 = 800 x 480像素
计算: 勾股定理 = (800 * y)^2 * (480 * y)^2 = 4^2 => y = 4.287464628
长宽尺寸 = (800 x 480) * y = 3.430 x 2.058英寸(87.1 x 52.3毫米)
(长)每英寸上有800/3.430=233个像素,每个像素尺寸87.1/800=0.109毫米
结论:显示屏由800x480=384000个像素组成,每个像素尺寸为0.109毫米。
##############################################################
(1)若图像大于显示屏,则需要滑动滚动条才能看完全图。
(2)若图像小于显示屏,则会居中显示,且无图显示处为黑框显示。
1.1.2、相机分辨率
人类毛发直径: 范围介乎0.017至0.18毫米之间。
人眼极限范围: 人的眼睛最小能看到0.02-0.01毫米粗细的小点,即PPI = 1270 x 2540
人眼视野范围: 单个眼睛,左右视野范围=160、上下视野范围=120
视角范围 = 160:120 = 4:3
因此,大部分相机的成像尺寸以此居多。还有5:4、16:10
##############################################################
相机分辨率(4:3) 15万像素 = 480 x 320 = 153600
20万像素 = 640 x 320 = 204800
30万像素 = 640 x 480 = 307200
50万像素 = 800 x 600 = 480000
80万像素 = 1024 x 768 = 786432
100万像素 = 1140 x 900 = 1026000
130万像素 = 1280 x 960 = 1228800
200万像素 = 1600 x 1200 = 1920000
300万像素 = 2048 x 1536 = 3145728
500万像素 = 2560 x 1920 = 4915200
800万像素 = 3264 x 2448 = 7990272
1000万像素 = 3648 x 2736 = 9980928
1200万像素 = 4000 x 3000 = 12000000
1400万像素 = 4228 x 3264 = 13800192
1.2、像元尺寸 —— 单个像素的物理尺寸(即:像素分辨率)
像元(Pixel):图像的最小单元,它代表了图像中的一个点(在图像中,又叫像素),具有一定的大小和灰度值。像元尺寸:每个像元在物理空间中的大小。
- 单位:用长度单位来表示(如:毫米、微米、纳米),取决于图像采集时所用的设备以及成像物体的尺寸。
- 作用:像元尺寸的大小对图像的分辨率和细节捕捉能力有着重要的影响。通常情况下,更小的像元尺寸能够提供更高的空间分辨率,因为它们能够更精细地捕捉到图像中的细节。
(相机)像素分辨率:单个像素的物理尺寸(像元尺寸)(相机)图像分辨率:单位距离内的" 像 ",需要多少个像素点来显示- 已知:相机的像元尺寸 = 6.5μm、物镜的放大倍率 = 40;即 1 μm 的 " 物 " 经光学系统放大后得到 40 μm 的 " 像 "。
- 可得:
- (1)
像素分辨率 = 像元尺寸 / 放大倍数 = 6.5(μm) / 40 = 0.162(μm / pixel)—— 单个 pixel 的物理尺寸为 0.162 μm- (2)
图像分辨率 = 放大倍数 / 像元尺寸 = 40 / 6.5(μm) = 6.15(pixel / μm)—— 单位 μm 距离内有 6.15 个pixel
1.3、信噪比
二、(显微镜)分辨率的影响因素:相机分辨率 + 光学分辨率
滨松相机:像元尺寸和光学分辨率的关系
在显微成像系统中,使用分辨率来评价其成像能力的好坏。
- (1)光学分辨率高 + 相机分辨率低,则实际分辨率会降低到图像分辨率以下;
- (2)光学分辨率低 + 相机分辨率高,则同样也看不清物体的精细结构。
2.1、(显微镜)分辨率的数学概念
2.1.1、数值孔径 —— 显微镜中物镜的重要参数
数值孔径(Numerical Aperture,NA):反映了物镜对进入显微镜的光线的采集能力和成像能力。
- 倒置成像:由于物镜对光线的折射性质,当物镜将光线聚焦到焦平面时,图像是倒置的。
焦平面 - 介绍:是距离物镜为一个焦距的平面。在焦平面上形成了一个倒置的、被物镜放大的图像。焦平面 - 功能:在焦平面上形成的图像会达到最佳的清晰度和焦距效果。
物镜的数值孔径NA越高,分辨率越好(与放大倍率无关)。
| 放大倍率(NA) | 显微镜的分辨率极限 |
|---|---|
| 4x(0.20) | 1.5 |
| 10x(0.45) | 0.64 |
| 20x(0.75) | 0.39 |
| 40x(0.85) | 0.34 |
| 40x(1.30) | 0.22 |
| 60x(0.95) | 0.31 |
| 60x(1.40) | 0.21 |
| 100x(0.90) | 0.32 |
| 100x(1.25) | 0.23 |
| 100x(1.40) | 0.21 |
2.1.2、艾里斑
艾里斑(Airy disk):光通过物镜,由于光学衍射效应,呈现出中心明亮、周围环绕暗环的光斑。
- 是光学显微镜中,点光源的成像结果(也是PSF的一种形式)
- 特征1:中央的亮斑被称为
艾里斑核(Airy disk core)- 特征2:周围的同心环被称为
艾里环(Airy rings)- 特征3:中心点包含大约84%的发光强度,其余16%围绕该点分布在衍射图样中。
2.1.3、阿贝的衍射极限 —— 解释了显微镜的衍射极限(艾里斑)
- 理论:图像是由(多个重叠的,多强度的)衍射极限点(或艾里斑)组成。
- 公式:
- 阿贝衍射极限(横向,即XY分辨率):
d = λ / (2 * NA)- 阿贝衍射极限(轴向,即Z分辨率):
d = 2 * λ / (NA^2)
- λ 为光的波长
- NA 为物镜的数值孔径
2.1.4、瑞利判据 —— 定义了衍射极限系统中的分辨率极限
- 理论:当两个艾里斑不断接近,直到肉眼不可分辨时,两个艾里斑的中心距离就是此物镜的分辨率(极限)。
- 公式:
NA = (1.22 * λ)/ (2 * NA) = (0.61 * λ)/ NA
以下为两个艾里斑的重叠衍射图,其显示了分辨率极限(由瑞利准则定义)
左:分辨率良好—— 两个单独的艾里斑不重叠中:分辨率极限—— 当一个艾里斑中心与另一个衍射图的第一个最小值直接重叠右:不具有分辨率—— 若艾里斑比中间的更近,不满足瑞利准则。
2.1.5、奈奎斯特采样定律 —— (理论上)最大采样步长 = 像元尺寸的一半
- 已知:显微镜的分辨率极限(样品端) = 0.22μm,物镜的放大倍率 = 100x
- 计算:放大后的分辨率极限(相机端) = 22μm
奈奎斯特采样定律(Nyquist):
(1)采样频率:若对一个连续信号进行采样并完全恢复出原始信号,则采样频率应该大于等于模拟信号频谱中最高频率的两倍
(2)采样周期:为了准确地重建信号,采样周期必须大于等于信号周期的两倍。
(3)采样步长:为了准确地重建信号,采样步长必须小于等于像元尺寸的一半。
- 采样周期:采样点之间的时间间隔,是采样步长的倒数。
根据奈奎斯特采样定律:
(1)当像元尺寸大于22μm的一半(11μm),相机无法分辨出间距在22μm以上的两个物体;
(2)当像元尺寸等于22μm的一半(11μm),可分辨。
(3)当像元尺寸小于22μm的一半(11μm),可分辨。
注意:像元尺寸并非越小越好
(相机)分辨率由像元尺寸和信噪比相互制约。
- (1)若相机的像元尺寸越小,则单位距离内的像素越多,分辨率越高。
- (2)若相机的像元尺寸越大,则落到一个像素上的光子就越多,信噪比越高。
2.2、光学分辨率 —— 两个像素的物理间距(即:两个艾里斑的中心距离)
-
系统的光学分辨率:指 " 物 " 在经过光学系统后的 " 像 "在细节上能被分辨的最小距离。 (极限的)光学分辨率:即:最小距离 = 瑞利判据的分辨率极限。
左(像素点) —— 中(艾里斑) —— 右(黑白条纹)
(左)光学分辨率:使用光学系统所能分辨的两个像素点的最小距离(瑞利判据)来表示。
- 第一行:
大于最小距离的两个像素点(左),两个艾里斑不重叠(中),经过光系统后会被识别为两个点(两个独立点);- 第二行:
等于最小距离的两个像素点(左),两个艾里斑重叠且距离达到瑞利判据的极限,经过光系统后仍会被识别为两个点(两个耦合点);- 第三行:
小于最小距离的两个像素点(左),两个艾里斑重叠且距离大于瑞利判据的极限(中),经过光系统后会被识别为一个点。(右)黑白条纹:间隔越宽的黑白条纹越容易分辨(类比艾里斑的重叠)。
2.2.1、光学系统 —— 低通滤波器(通低频阻高频)
-
光学系统:可以看作是一个空间上的低通滤波器(通低频阻高频),故从 " 物 " 到 " 像 " 的过程中会发生 " 失真 " 。
通俗理解:削弱了由" 黑 “到” 白 "的锐度和对比度,使其变得平滑和模糊。
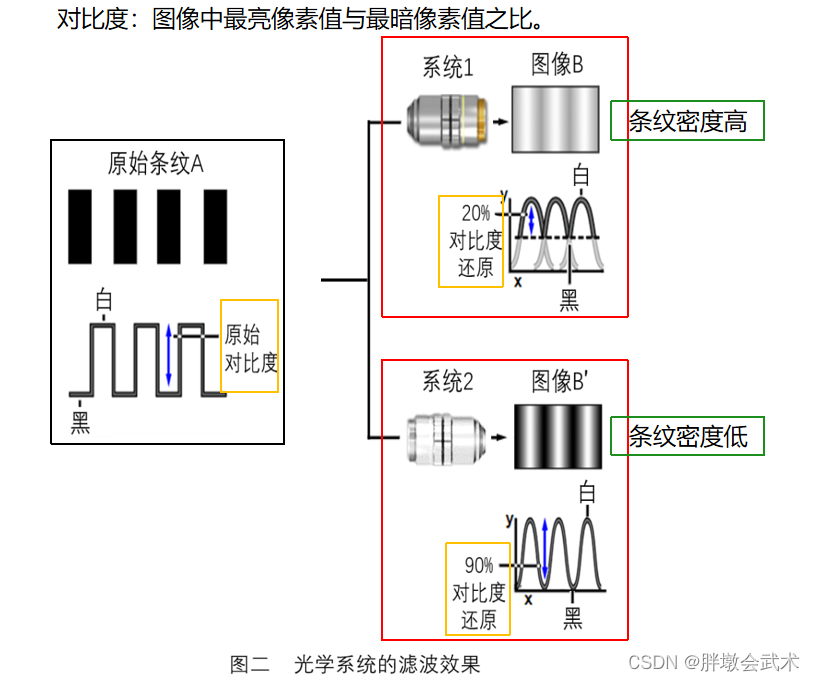
(左)原始条纹A:使用黑白表示灰度值(0 / 255),并构成一个方波信号。(右上)图像B:经过系统1,条纹密度变高(宽)。使得展宽的峰互相交叠,导致重叠部分的对比度下降(20%)。(右下)图像B':经过系统2,条纹密度变低(细)。保留了更多的高频信号,使得信号的变化斜率更大,对比度更接近真实(90%)。
2.2.2、(极限的)光学分辨率 —— 瑞利判据的分辨率极限
- 光学上的极限分辨率(理论值)
= 瑞利判据公式 = 0.61 * λ / NA- λ为波长(对于荧光显微镜,就是荧光探针的发射波长);
- NA为物镜的数值孔径(可以在物镜上找到);
连续信号的离散采样:相机芯片在x方向上以像元尺寸为单位距离,均匀对曲线作积分,得到每个像素值。
相机芯片上的像素以固定距离排列,而采样频率越高,则空间周期(d)越短。
采样周期(I):表示像元尺寸采样频率:表示单位距离内像素点的个数(即:白色/黑色条纹重复出现的频率)空间周期(d):表示光学分辨率(如:条纹间距、像素间距)
- (光学分辨率 × 放大倍率):表示 " 物 " 点在经过物镜放大后的 " 像 " 点的距离。
- 像元尺寸(I) = 放大倍率 * 光学分辨率 / 2
2.2.3、(实际的)光学分辨率 —— 木桶 - 短板效应
-
木桶 - 短板效应:在整个成像系统分辨率上(木桶),光学分辨率和图像分辨率就好比木桶上的两块木板,最终成像系统的分辨率等于短板的那一个。
举例:一台荧光显微镜,采用NA = 1.4的63倍油浸镜,光路中没有其他放大;观察λ = 509nm的荧光样本。
- 相机类型1:像元尺寸 = 6.5 um
- 光学分辨率 = 0.61 * 509 nm / 1.4 = 222 nm(不变)
- 图像分辨率 = 2 * 6.5 um / 63 =
206 nm
- 结论:由于光学分辨率差(数值越大,分辨率越低),故整个系统的分辨率是受限于光学分辨率( = 222 nm)。
- 相机类型2:像元尺寸 = 11 um
- 光学分辨率 = 0.61 * 509 nm / 1.4 = 222 nm(不变)
- 图像分辨率 = 2 * 11 um / 63 =
349 nm
- 结论:由于图像分辨率差(数值越大,分辨率越低),故整个系统的分辨率是受限于图像分辨率( = 349 nm)。
(实际的)像元尺寸应该小于(理想的)像元尺寸,像元尺寸越小对细节的解析越好,但小于理想值的1/2就无显著性改善了。
(相机)分辨率由像元尺寸和信噪比相互制约。
- (1)若相机的像元尺寸越小,则单位距离内的像素越多,分辨率越高。
- (2)若相机的像元尺寸越大,则落到一个像素上的光子就越多,信噪比越高。






































 1306
1306

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










