为什么计数应该从零开始?
2013-06-15 06:36
众所周知,C 语言数组下标是从 0 开始,其它很多语言皆如此。而 FORTRAN 则是数组下标从 1 开始的典范。所以就有数组下标是从 1 开始好还是从 0 开始好之争。连《C 专家编程》中都如此调侃:
数组的下标应该是从 0 还是从 1 开始?我提议的妥协方案是 0.5,可惜他们未予认真考虑便一口回绝。—— Stan Kelly-Bootle
仔细思考一下这个问题很有意思,建议你不妨自己思考一下再继续往下看。
其实这个问题早在 1982 年就已经由计算机科学领域的大师 Edsger Dijkstra. 研究过并得出了一个结论。他手写了一篇名为《Why numbering should start at zero》的论文,关键部分截图和大体翻译如下:


表示一个自然数子序列,比如 2, 3, …, 12,不用中间那三个点,有四种方式可供我们选择:
a) 2<= i < 13
b) 1 < i <= 12
c) 2<= i <= 12
d) 1 < i < 13
有什么道理选其中一种而不选别的吗?是的,的确有。观察到 a) 和 b) 的优势是两边的边界值之差正好是子序列的长度。作为一个推论,下面的观察也成立:在它们两个当中,两个子序列是邻接的就意味着一个的上界等于另外一个的下界。这些观察并没有让我们从 a) 和 b) 之中做出选择,所以我们从头开始。
一定存在一个最小的自然数。排除掉下界 —— 就像 b) 和 d) 那样 —— 就会迫使一个从最小的自然数开始的子序列的下界进入非自然数领域。这很难看,所以对于下界我们更喜欢 <=,就像 a) 和 c) 那样。现在,考虑一下从最小的自然数开始的子序列:包含上界就会迫后者不那么像自然数(译者注:作者的意思是自然数是一个有下界没有上界的集合),当序列缩小成空序列时。这很难看,所以对于上界我们更喜欢 <,就像 a) 和 d) 那样。我们得出结论, a) 是我们最喜欢的。

当处理长度为 N 的序列时,我们期望通过下标来区分它的元素。下一个令人烦恼的问题就是,我们该给它的第一个元素赋予什么样下标值?坚持 a) 的方式,当下标从 1 开始时,下标范围为 1<= i < N+1;当下标从 0 开始时则是更好看的 0<= i < N。所以,让我们的序数从 0 开始:一个元素的序数(下标)等于序列中在它前面的元素个数。这个故事的寓意是我们最好尊重 0 最为一个最自然的数 —— 过了这么多个世纪!
———
顺便说一句,Python 选择了 a),所以 range (0,3) 返回的是序列是 0,1,2。
漫话:为什么程序员喜欢使用 0 ≤ i < 10 这种左闭右开的形式写 for 循环?
原创 漫话编程 2020 年 06 月 29 日 12:14








当我们想要写一个循环体,期望执行 10 次的时候,我们会使用以下方式:
for (int i=0; i<10; i++){
}
可以看到,为了保证循环 10 次,我们定义了一个整数变量从 0 开始,然后循环 10 次,结束条件是 i < 10。
其实这个本质就是使用了 0 ≤ i < 10 这种表达形式。
之所以很多人都这么写,有一个最主要的原因就是刚开始学编程的时候,老师都是这么教的…




关于这个问题,其实还有一位伟大的数学家曾经讨论过他的合理性。
这个人就是 Dijkstra,他也是离散数学中应用广泛的最短路径算法的提出者,并且还提出了银行家算法。
他在 1982 年发表了一篇说明《Why numbering should start at zero》,这里面有部分内容阐述了这个观点。
他首先提出一个问题,让我们通过一个条件表达式表示 2,3,4,5,6,7,8,9,10,11,12 这 11 个数字,其实一般有以下四种写法:
-
a) 2 ≤ i < 13
-
b) 1 < i ≤ 12
-
c) 2 ≤ i ≤ 12
-
d) 1 < i < 13
这几种也是我们在写 for 循环的时候可能会用到的一些表示式,那着四种写法有没有好坏之分呢?
答案是有的。



我们其实可以观察到,a) 和 b) 有个优点,上下边界的相减得到的差,正好等于子序列的长度,即 13-2 = 12-1 = 11; 这样的写法可以让我们快速知道这个表示表达式中一共包含多少个自然数。
当然,这并不是正菜,只是开胃而已…
接下来,Dijkstra 分别从表达式的上下界讨论了到底使用 ≤ 还是 < 更合理。
首先,他论证了一下表达式的下界使用哪种形式合理。
他认为,当我们想要表达自然数 2-12 的时候,如果使用 1 < i 作为这个序列的下界的话,这个下界的起始值进入了非自然数的区域。而使用 2 ≤ i,那么就可以严格的保证这个下界就是一个自然数 2 。所以,他认为下界使用 ≤ 更加合理。
符合这种形式的就是 a) 和 c) 两种。
那么 a) 和 c) 还有一个区别,就是上界一个用了 ≤ 一个用了 <,那该使用哪种方式更加合适呢?
Dijkstra 提出,如果想要表达一个空序列,使用 a) 形式可以很容易的表达,如 0<= i <0 就可以表示一个空序列。
但是如果上界和下界都用 <= 就无法表示了,除非用 1 <= i <= 0,但是这种形式就很不合逻辑。
所以,综上,他认为 a) 2 ≤ i < 13 这种表达方式更加合理一些。
也就是说,使用左闭右开的形式定义表达式合理也更加优雅!


漫画:为什么计算机从 0 开始计数,而不是从 1 开始?
原创 漫话编程 2020 年 07 月 13 日 12:00





当我们想要写一个循环体,期望执行 10 次的时候,我们会使用以下方式:
for (int i=0; i<10; i++){
}
可以看到,为了保证循环 10 次,我们定义了一个整数变量从 0 开始。
还有,当我们定义数组的时候,在常见的 C 语言、Java、Python 等语言中,都是使用下标 0 来表示第一个元素的。


从 0 开始更优雅
在《为什么程序员喜欢使用 0 ≤ i < 10 这种左闭右开的形式写 for 循环?》一文中我们分析过,Dijkstra 通过分析,得出在进行范围表达的时候,使用左闭右开的方式更加合理。
但是,Dijkstra 在分析出 2 ≤ i < 13 这种形式更加合理之后,他有陷入了另外一个思考,那就是:
当处理长度为 N 的序列时,到底第一个元素的下标使用 0 还是 1 更加合适?
关于这个分析,他的出发点很简单,那就是哪种方式更加漂亮,更加优雅。
他认为,使用左闭右开的表达方式,当下标从 1 开始时,下标范围为 1 <= i < N+1;当下标从 0 开始时则是 0 <= i < N;
而显然后面这种表达式更加漂亮、优雅一些。所以,他建议我们使用 0 作为第一个下标。




计数表示偏移量
很多人学习编程都是从 C 语言开始的,那么,C 语言就是一个典型的 0-base 语言(以 0 作为计数的开始),其实,这一约定早在 BCPL 时代就是这样的了。
在 C 语言还不叫 C 语言,还叫 BCPL 的时候,他的作者马丁・理察德就设计了数组从 0 开始的索引方式。
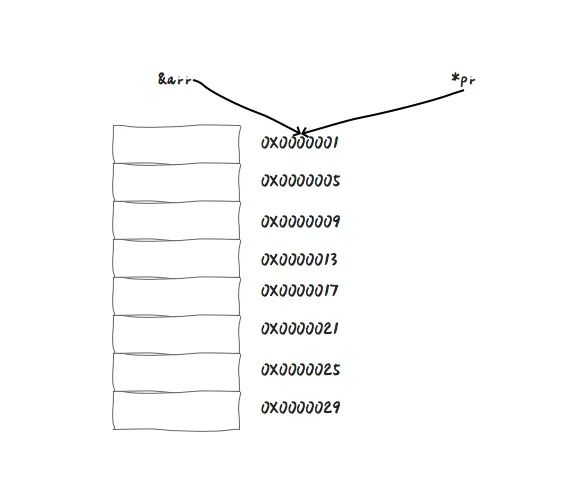
当我们在 BCPL(C 语言)中定义数组 int arr[8] 的时候,编辑器会在内存中开辟一块空间(这个空间中可能包含多个内存单元)供该数组使用。
为了能让数组找到编译器为自己开辟的空间,会把这块内存空间中第一个内存单元的地址 (0X0000001) 赋值给这个数组,当我们使用 & arr 的时候,就可以拿到这块地址。
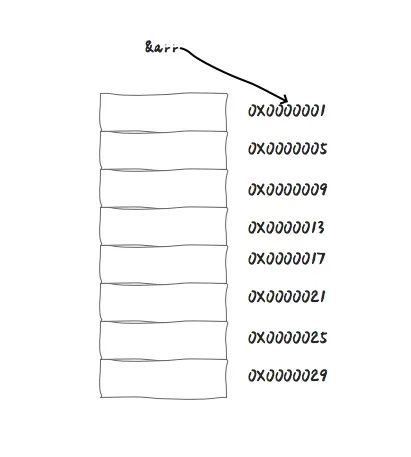
BCPL 最初是用 IBM 7094 机器编译的;它在编译时会优化这些数组索引提供的 **指针反参考运算 **(indirection),即可以通过指针取出地址中存储的值,这个特性也一直延续到今天。
有了指针之后,我们可以使用 int *pr = arr 的方式初始化一个指针,那么,这时候,指针 pr 也会指向数组的内存空间的第一个内存单元的地址。
那有了数组和指针,想要使用这块内存第一个内存单元存储一个变量的时候,就需要想办法表示这第一个空间。
那么,BCPL 的作者采用了 0 作为数组第一个元素的下标,因为他认为,数组的下标应该和指针的偏移量是相对应的。这样在使用第一个内存单元的时候,直接使用 arr[0] 或者 *(p+0) 就可以了。
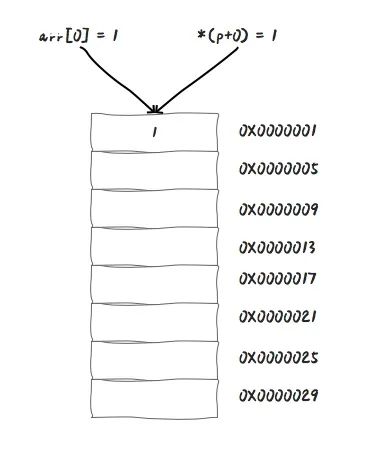


因为指针 *(p+0) 这种表达形式中的 0 表示的是偏移量,所以,无论数组的下标从几开始,*(p+0) 都是用于存取内存中的 p+0 位址的值,也就是 0X0000001 这块内存单元的值。
试想一下,如果使用 1 作为数组的起始下标,那么 arr1 就应该指向 0X0000001 这块内存,但是 *(p+1) 按照偏移量的计算方式,需要指向 0X0000005 这块内存。这种情况下,如果想要让 *(p+1) 和 arr[1] 指向同一块内存,就需要额外做一次减法指令。
因为几乎所有计算机结构,都借由位址和偏移量来表示直接引用内存,所以,像 C 语言这种使用 0 做为数组的第一个下标使得语言的实现上更加容易。
但是值得一提的是,在 C 语言流行起来之前,还是有很多 1-base 的编程语言的,如 FORTRAN、BASIC 等编程语言的数组下标都是从 1 开始的。
随着 C 语言的发扬光大,很多语言都参考了 C 语言的做法。



Python 作者的解释
关于这个问题,之前也有网友在 Twitter 上询问过 Python 之父 ——Guido van Rossum,他给出过正面回答,我把回答内容的翻译版贴在下面:
我记得自己就这个问题思考过很久;Python 的祖先之一 ABC 语言,使用的索引是从 1 开始的(1-based indexing),而对 Python 语言有巨大影响的另一门语言,C 语言的索引则是从 0 开始的。
我最早学习的几种编程语言 (Algol, Fortran, Pascal) 中的索引方式,有的是 1-based 的,有的是从定义的某个变量开始(variable-based indexing)。而我决定在 Python 中使用 0-based 索引方式的一个原因,就是切片语法 (slice notation)。
让我们来先看看切片的用法。可能最常见的用法,就是 “取前 n 位元素” 或 “从第 i 位索引起,取后 n 位元素”(前一种用法,实际上是 i== 起始位的特殊用法)。如果这两种用法实现时可以不在表达式中出现难看的 + 1 或 - 1,那将会非常的优雅。
使用 0-based 的索引方式、半开区间切片和缺省匹配区间的话(Python 最终采用这样的方式),上面两种情形的切片语法就变得非常漂亮:a[:n] 和 a[i:i+n],前者是 a[0:n] 的缩略写法。
如果使用 1-based 的索引方式,那么,想让 a[:n] 表达 “取前 n 个元素” 的意思,你要么使用闭合区间切片语法,要么在切片语法中使用切片起始位和切片长度作为切片参数。
半开区间切片语法如果和 1-based 的索引方式结合起来,则会变得不优雅。
而使用闭合区间切片语法的话,为了从第 i 位索引开始取后 n 个元素,你就得把表达式写成 a[i:i+n-1]。
这样看来,1-based 的索引方式,与切片起始位 + 长度的语法形式配合使用会不会更合适?这样你可以写成 a[i:n]。事实上,ABC 语言就是这样做的 —— 它发明了一个独特的语法,你可以把表达式写成 a@i|n。
但是,index:length 这种方式在其它情况下适用吗?说实话,这点我有些记不清了,但我想我是被半开区间语法的优雅迷住了。
特别是当两个切片操作位置邻接时,第一个切片操作的终点索引值是第二个切片的起点索引值时,太漂亮了,无法舍弃。
例如,你想将一个字符串以 i,j 两个位置切成三部分,这三部分的表达式将会是 a[:i],a[i:j] 和 a[j:]。



漫话:为什么计算机用补码存储数据?
原创 漫话编程 2020 年 08 月 31 日 12:04





我们知道,计算机只认识 0 和 1,现实世界中的内容,无论是文字、音频、视频等等想要通过计算机存储、计算或者展示,都需要转换二进制。
就像你刚刚唱的旋律,想要存储在计算机中也是要转成二进制的。
那么,最简单的一个数字,想要在计算机中表示出来,就需要通过一定的手段将他转换成二进制。而这种手段我们称之为编码方式。





原码
相信很多人在上初中的时候都学过很多方式把一个十进制数转成二进制数,比如我们可以很快速的知道 10 的二进制可以表示成 1010 。
但是初中老师没有告诉我们的是:-10 如何表示呢?
为了在计算机中想办法表示负数。于是人们想出来一种办法:
在二进制数值前面增加一位符号位(即最高位为符号位):正数该位为 0,负数该位为 1,其余位表示数值的大小。
这样,如果我们想要 10 的话,那么就应该是:0 1010,想要表示 - 10 的话,就应该是 1 1010。
这种编码方式被称之为原码,原码的优点比较明显,那就是非常的简单直观,很容易被人理解。

使用原码,解决了十进制在计算机中的存储问题,但是计算机中还有一个重要的操作那就是计算。使用原码如何计算呢?
首先,原码对于加法的运算是没什么问题的,如 5 + 2 :
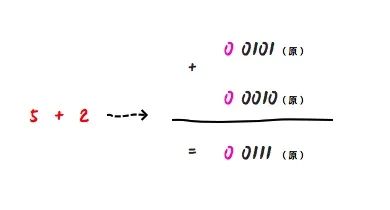
对应的二进制运算:0 0101(原) + 0 0010(原) = 0 0111(原) 其对应的十进制是 7。
加法没什么问题,那么我们再试着用原码来计算减法,例如我们想要计算 10 - 2:
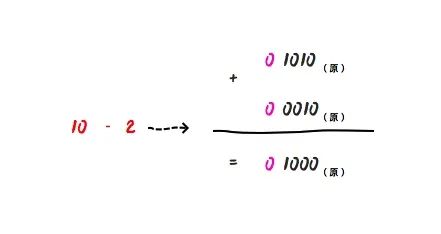
那么就是 0 1010(原) - 0 0010(原) = 0 1000(原),那么这个二进制对应的十进制刚好是 8。可见原码计算减法没有问题的?
但是,以上运算只是我们一厢情愿的算法,其实计算机算术逻辑单元(ALU)并没有直接进行减法运算,对于减法,其实也是用加法器来实现的。
也就是说,计算机中的所有的减法运算都需要转换成加法运算,那么 10 - 2 其实就是 10 + (-2):
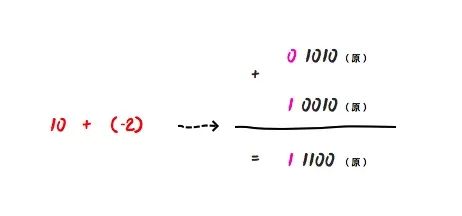
他们的二进制 0 1010 (原) + 1 0010 (原) = 1 1100 (原) ,得到的结果考虑他的符号位的话,这个值是 - 12,这明显是错误的!
可见,原码虽然对于人类来说是比较简单直观的,但是对于计算机来说却带来了很大的计算难度。


反码
因为原码虽然容易被人理解,但是给计算机的计算带来了一定的困难,尤其是减法的运算。所以,人们发明出反码来解决减法运算的问题。
反码是基于原码计算得来的,表示方式是:正数的反码是其本身。负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
如,10 的 原码为 0 1010 ,那么他的反码同样也是 0 1010 。
如,-2 的原码为 1 0010 ,那么他的反码为 1 1101 。
有了反码之后,二进制的运算就可以带着符号位一起了。并且可以直接将减法转换成加法进行运算。但是使用反码进行运算,需要注意以下几点:
-
反码运算时,其符号位与数值一起参加运算。
-
反码的符号位相加后,如果有进位出现,则要把它送回到最低位去相加(循环进位)。
-
用反码运算,其运算结果亦为反码。在转换为真值时,若符号位为 0,数位不变;若符号位为 1,应将结果求反才是其真值。
如 10 - 2 的在计算时需要转成 10 + (-2) 进行计算:
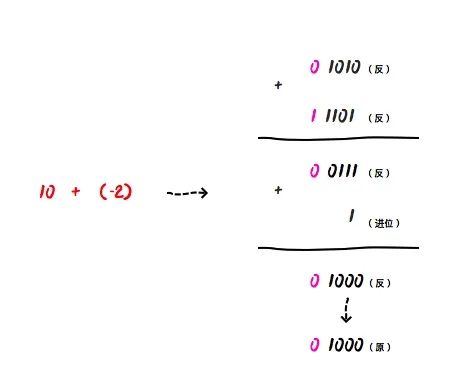
0 1010(反) + 1 1101(反) = 0 0111(反) + 1 (进位) = 0 1000 ,因为符号位是 0,表示正数,所以他对应的原码也是 0 1000(原),则十进制值为 8。
那么,我们再来计算法 2 - 10 ,把 2 - 10 转换成 2 + (-10)进行计算:
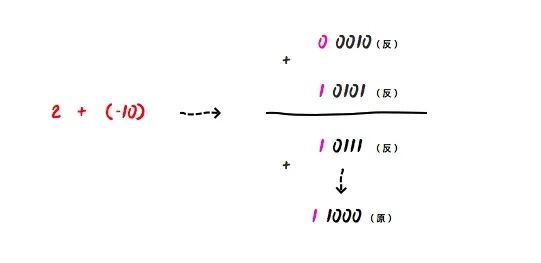
0 0010(反) + 1 0101(反) = 1 0111(反),因为符号位是 1,表示负数,所以他对应的原码也是 1 1000(原),则十进制为 - 8。
以上,我们通过几个例子展示了反码,我们知道使用反码进行计算的时候,可以带着符号位一起计算,只需要在计算之后再将反码转换成原码,再计算其对应的十进制就可以了。
但是,反码运算还是有一个小问题,我们看一下下面这个例子:
我们尝试计算 10 - 10 ,即 10 + (-10):
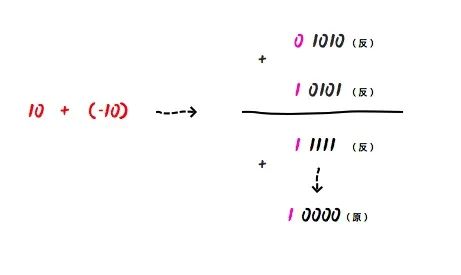
0 1010(反) + 1 0101(反) = 1 1111(反),因为符号位是 1,表示负数,所以他对应的原码也是 1 0000(原),则十进制为 - 0。
虽然很多人够能够理解 + 0 和 - 0 其实是一样的,但是 0 带符号仍然是没有任何意义的。
如果一台计算机有 8 位,我们想要用反码表示 0 的话,就有 0000 0000 和 1111 1111 两种方式,分别表示 + 0 和 - 0。



补码
虽然反码解决了减法的问题,但是对于 0 的符号问题却没有解决,于是补码出现了。
补码是在原码和反码的基础上衍生出来的,补码的表示方法是:正数的补码就是其本身,负数的补码是在其原码的基础上, 符号位不变, 其余各位取反,最后 + 1。(即在反码的基础上 + 1)
补码计算的规则:
-
补码运算时,其符号位与数值一起参加运算。
-
补码的符号位相加后,如果有进位出现,则进位被舍弃。
-
用反码运算,其运算结果亦为补码。在转换成原码时,如果是正数,其补码就是原码;如果是负数,该补码的补码就是其原码。
我们再来用补码的方式,来计算下 10 - 10 :
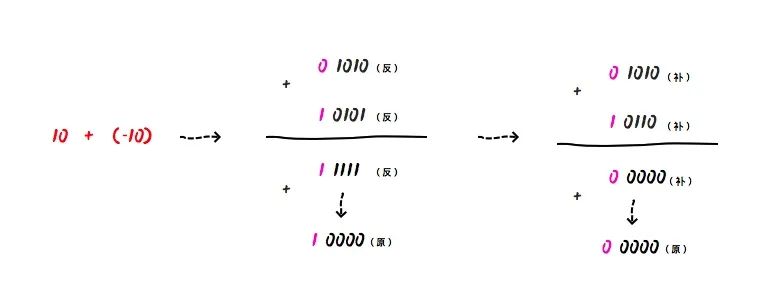
01010(补) + 10110(补) = 0 0000 (补),因为符号位是 0,表示正数,所以他对应的原码也是 0 0000(原),则十进制为 0。
有了补码,0 的表达方式就唯一了,如果是 8 位的话,那么就是固定的 0000 0000。
如果使用原码或者反码,8 位的原码或者反码能表示的最小数字是 - 127,而使用补码,能表示的最小数字是 - 128。
可见,使用补码,不仅仅修复了 0 的符号以及存在两个编码的问题,而且还能够多表示一个最低数。这就是为什么 8 位二进制,使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127]。



使用补码的原因
通过以上介绍,我们知道了原码、反码和补码的一些知识,我们尝试着总结下为什么计算机中会最终选择补码来进行存储和计算数字。
1、计算机的运算器为了实现简单,倾向于在运算过程中将减法转换成加法,统一使用加法运算器进行计算。想要把减法转化成加法运算,就需要在运算时带着符号一起运算,而反码和补码可以带符号位一起运算,也就方便了将减法转换为加法。
2、采用补码,可以解决编码中有 + 0 和 - 0 两种表示 0 的方式。
3、补码表示的数字范围要比原码和反码大。如 8 位 2 进制,使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127]。






via
-
为什么计数应该从零开始? - A Geek’s Page Posted in Programming at January 26th, 2013
-
漫话:为什么程序员喜欢使用 0 ≤ i < 10 这种左闭右开的形式写 for 循环? 原创 漫话编程 2020 年 06 月 29 日 12:14
-
漫话:如何给女朋友解释为什么计算机从 0 开始计数,而不是从 1 开始?原创 漫话编程 2020 年 07 月 13 日 12:00
-
漫话:为什么计算机用补码存储数据?原创 漫话编程 2020 年 08 月 31 日 12:04



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








