注:本文为 “时间度量” 相关文章合辑。
英文引文,机翻未校。
中文引文,未整理。
What is time?
什么是时间?
By Jonathan O’Callaghan
last updated August 26, 2022
Time is all around us, but how exactly does it work?
时间就在我们身边,但它究竟是如何运作的呢?

Time is all around us, a constant that keeps the world and universe ticking. (Image credit: Shutterstock)
时间就在我们身边,是让世界和宇宙持续运转的一个常量。
From the beginning of the universe to the present day, time is one of the few things we regard as regular and unchanging. Time works by measuring periods between the past, present and future.
从宇宙的开端到如今,时间是我们认为有规律且不变的少数事物之一。时间通过测量过去、现在和未来之间的时间段来运作。
But that’s a simple, albeit vague answer to an incredibly complex topic.
但对于一个极其复杂的话题而言,这是一个简单却又模糊的答案。
Time is all around us and is the basis of how we record life on Earth_. Civilizations rise and fall, stars are born and extinguished, and our method of tracking how those moments relate to the present remains unchanged. But time is not as constant nor as simple as it may seem.
时间就在我们身边,是我们记录地球上生命的基础。文明兴衰交替,恒星诞生又消亡,而我们追踪那些时刻与当下关系的方法却始终不变。但时间并不像看起来那样恒定,也没有那么简单。
In the 17th century, physicist saac Newton_. saw time as an arrow fired from a bow, traveling in a direct, straight line and never deviating from its path. To Newton, one second on Earth was the same length of time as that same second on Mars_, Jupiter_ or in deep space. He believed that absolute motion could not be detected, which meant that nothing in the universe had a constant speed, even light. By applying this theory, he was able to assume that if the speed of light_ could vary, then time must be constant. Time must tick from one second to the next, with no difference between the length of any two seconds. This is something that it’s easy to think is true. Every day has roughly 24 hours; you don’t have one day with 26 and one with 23.
在 17 世纪,物理学家艾萨克·牛顿(Isaac Newton)将时间看作是从弓上射出的一支箭,沿直线径直飞行,从不偏离其路径。对牛顿来说,地球上的一秒与火星(Mars)、木星(Jupiter)或深空里的一秒时长是一样的。他认为绝对运动是无法检测到的,这意味着宇宙中没有任何东西具有恒定的速度,甚至连光也没有。通过应用这一理论,他能够假定如果光速(speed of light)可以变化,那么时间一定是恒定的。时间必定从一秒滴答走到下一秒,任意两秒的时长之间没有差别。这是很容易让人觉得正确的观点。每天大致有 24 小时;你不会遇到一天有 26 小时,而另一天有 23 小时的情况。
However, in 1905, Albert Einstein_ asserted that the speed of light doesn’t vary_, but is a constant, traveling at 186,282 miles per second (299,792 kilometers per second). He postulated that time was more like a river, ebbing and flowing depending on the effects of gravity_ and space-time. Time would speed up and slow down around cosmological bodies with different masses and velocities, and therefore one second on Earth was not the same length of time everywhere in the universe.
然而,在 1905 年,阿尔伯特·爱因斯坦(Albert Einstein)断言光速(speed of light doesn’t vary)不会变化,而是一个常量,以每秒 186,282 英里(每秒 299,792 公里)的速度传播。他假设时间更像是一条河流,会根据引力(gravity)和时空的影响而涨落。在不同质量和速度的天体周围,时间会加速或减慢,因此地球上的一秒在宇宙中的任何地方时长都不一样。
Decades later, Einstein’s theory was proven to be true. In October 1971, physicists J.C. Hafele and Richard Keating tested Einstein’s theory by flying four cesium atomic clocks on planes around the world, going eastwards and then westwards.
几十年后,爱因斯坦的理论被证明是正确的。1971 年 10 月,物理学家 J.C. 哈费勒(J.C. Hafele)和理查德·基廷(Richard Keating)通过让四个铯原子钟搭载飞机环绕世界飞行来测试爱因斯坦的理论,飞机先向东飞,然后向西飞。
In their paper published in 1972 in the journal Science, Hafele and Keating reported that the airborne clocks were about 59 nanoseconds slower than a ground-based atomic clock when traveling east, and 273 nanoseconds faster than the ground-based version when traveling west. Their results supported Einstein’s theory that time fluctuates throughout the universe.
在 1972 年发表于《科学》杂志的论文中,哈费勒和基廷报告称,向东飞行时,机载时钟比地面原子钟慢约 59 纳秒,向西飞行时则比地面原子钟快 273 纳秒。他们的结果支持了爱因斯坦关于时间在整个宇宙中会波动的理论。
How long is a second?
一秒有多长?
There are two main ways of measuring time: dynamic and atomic time. The former relies on the motion of celestial bodies, including Earth, to keep track of time, whether it’s the rotation time of a distant spinning star such as a pulsar_, the motion of a star across our night sky or the rotation of Earth. However, a spinning star notwithstanding, these methods are not always entirely accurate.
测量时间主要有两种方式:动态时间和原子时间。前者依靠包括地球在内的天体的运动来记录时间,无论是像脉冲星(pulsar)这样遥远的旋转恒星的自转时间、恒星在我们夜空的移动,还是地球的自转。然而,尽管有旋转的恒星,这些方法并不总是完全准确的。
The old definition of a second was based on the rotation of Earth. As it takes the sun one day to rise in the east, set in the west and rise again, a day was almost arbitrarily divided into 24 hours, an hour into 60 minutes and a minute into 60 seconds. However, Earth doesn’t rotate uniformly. Its rotation decreases at a rate of about 30 seconds every 10,000 years due to factors such as tidal friction_. Scientists have devised ways to account for the changing speed of Earth’s rotation, introducing leap seconds, but for the most accurate time you have to go even smaller.
秒的旧定义基于地球的自转。因为太阳从东方升起、在西方落下然后再次升起需要一天的时间,一天几乎被随意地划分为 24 小时,一小时分为 60 分钟,一分钟又分为 60 秒。然而,地球的自转并不均匀。由于潮汐摩擦(tidal friction)等因素,地球的自转速度以每 10,000 年约 30 秒的速率减慢。科学家们已经想出了一些方法来解释地球自转速度的变化,引入了闰秒,但要获得最精确的时间,你必须采用更微观的方法。
Atomic time relies on the energy transition within an atom of a certain element, commonly cesium. By defining a second using the number of these transitions, time can be measured with an accuracy of losing a tiny portion of a second in a million years. The definition of a second is now defined as 9,192,631,770 transitions within a cesium atom, Scientific American_ reported.
原子时间依赖于某种元素(通常是铯)原子内的能量跃迁。通过用这些跃迁的次数来定义一秒,时间的测量精度可以达到在一百万年里仅损失极小一部分秒。据《科学美国人》(Scientific American)报道,现在一秒的定义是铯原子内的 9,192,631,770 次跃迁。
Atomic clocks: The most accurate track of time
原子钟:最精确的时间记录方式
Atomic clocks_ provide the most accurate track of time on Earth. The entire GPS system_ in orbit around Earth uses atomic clocks to accurately track positions and relay data to the planet, while entire scientific centers are set up to calculate the most accurate measure of time — usually by measuring transitions within a cesium atom.
原子钟(Atomic clocks)提供了地球上最精确的时间记录方式。环绕地球轨道运行的整个全球定位系统(GPS system)都使用原子钟来精确跟踪位置,并将数据传输回地球,而整个科学中心的设立是为了计算最精确的时间测量值——通常是通过测量铯原子内的跃迁来实现。
While most atomic clocks rely on magnetic fields_, modern clocks are using lasers to track and detect energy transitions within cesium atoms and keep a more definite measure of time. Although cesium clocks are currently used to keep time around the world, strontium clocks promise twice as much accuracy, while an experimental design based on charged mercury atoms could reduce discrepancies even further to less than one second lost or gained in 400 million years.
虽然大多数原子钟依赖于磁场,但现代原子钟正在使用激光来跟踪和检测铯原子内的能量跃迁,并更精确地测量时间。尽管目前世界各地都使用铯钟来计时,但锶钟的精度预计是铯钟的两倍,而基于带电汞原子的实验设计可以将误差进一步缩小到在 4 亿年里的时间误差不到一秒(无论是多一秒还是少一秒)。
Time: The fourth dimension of the universe
时间:宇宙的第四维度
Scientists once thought that space and time were separate, and that the universe was merely an assortment of cosmic bodies arranged in three dimensions. Einstein, however, introduced the concept of time as the fourth dimension, which meant that space and time were inextricably linked. His general theory of relativity_ suggests that space-time expands and contracts depending on the momentum and mass of nearby matter.
科学家们曾经认为空间和时间是相互独立的,宇宙仅仅是由以三维形式排列的各种天体组成的集合。然而,爱因斯坦引入了时间作为第四维度的概念,这意味着空间和时间是紧密相连、不可分割的。他的广义相对论(general theory of relativity)表明,时空会根据附近物质的动量和质量而膨胀和收缩。
Many years after its proposal, Einstein’s theory of general relativity was proven thanks to NASA’s Gravity Probe B, which demonstrated that space and time were indeed linked. Four gyroscopes were pointed in the direction of a distant star, and if gravity did not have an effect on space and time, they would remain locked in the same position. However, scientists clearly observed a “frame-dragging” effect due to the gravity of Earth, which meant the gyroscopes were pulled very slightly out of position. This suggests that the fabric of space can be altered, and if space and time are linked, then time can be stretched and contracted by gravity.
在爱因斯坦提出广义相对论多年后,这一理论得到了证实,这要归功于美国国家航空航天局(NASA)的引力探测器 B,它证明了空间和时间确实是相互关联的。四个陀螺仪被指向一颗遥远恒星的方向,如果引力对空间和时间没有影响,它们就会保持在相同的位置。然而,科学家们清楚地观察到了由于地球引力产生的“框架拖曳”效应,这意味着陀螺仪被轻微地拉离了原来的位置。这表明空间的结构是可以改变的,如果空间和时间是相互关联的,那么时间就可以在引力的作用下被拉伸和压缩。
Why time moves only forward
为什么时间只向前流动
Although Newton and Einstein came up with conflicting theories to explain how time works, both scholars agreed that time moves only forward. So far, there is no physical evidence that anything in the universe can dodge time and move backwards nor jump ahead. And scientists aren’t entirely sure why time moves only forward, but they have theories.
尽管牛顿和爱因斯坦提出了相互矛盾的理论来解释时间是如何运作的,但两位学者都认同时间只会向前流动。到目前为止,没有任何物理证据表明宇宙中的任何事物能够避开时间而向后移动或向前跳跃。科学家们也并不完全确定为什么时间只会向前流动,但他们提出了一些理论。
One theory relies on the second law of thermodynamics_. This law states that everything in the universe tends to move from low to high entropy, or from uniformity to disorder, beginning with simplicity at the Big Bang_ and moving to the almost random arrangement of galaxies_ and their inhabitants in the present day. This is known as the “arrow of time,” or sometimes “time’s arrow,” likely coined by British astronomer Arthur Eddington in 1928, analytic philosopher Huw Price said at Séminaire Poincaré in 2006_.
有一种理论依赖于热力学第二定律(second law of thermodynamics)。这条定律指出,宇宙中的一切事物都倾向于从低熵状态向高熵状态转变,或者说从有序状态向无序状态发展,从大爆炸(Big Bang)时的简单状态开始,发展到如今星系(galaxies)及其组成部分近乎随机的排列状态。这被称为“时间之箭”,有时也叫“时间箭头”,分析哲学家休·普莱斯(Huw Price)在 2006 年的庞加莱研讨会(Séminaire Poincaré in 2006)上表示,这个术语很可能是由英国天文学家阿瑟·爱丁顿(Arthur Eddington)在 1928 年创造的。
Eddington suggested that time was not symmetrical: “If as we follow the arrow we find more and more of the random element in the state of the world, then the arrow is pointing towards the future; if the random element decreases, the arrow points towards the past,” he wrote in “The Nature of the Physical World” in 1928. For example, if you were to observe a star in almost uniformity, but later saw it explode as a supernova_ and become a scattered nebula, you would know that time had moved forward from equality to chaos.
爱丁顿认为时间是不对称的:“如果当我们顺着箭头的方向,发现世界状态中的随机元素越来越多,那么箭头就指向未来;如果随机元素减少,箭头则指向过去。” 他在 1928 年所著的《物理世界的本质》(The Nature of the Physical World)一书中这样写道。例如,如果你观察到一颗几乎处于均匀状态的恒星,后来却看到它像超新星(supernova)那样爆炸并变成了一个分散的星云,你就会知道时间已经从有序走向了无序。
Another theory suggests that the passage of time is due to our expanding universe_. As the universe expands, it pulls time with it because space and time are linked as one. But this implies that if the universe were to reach a theoretical limit of expansion and begin to contract, then time would reverse — a slight paradox. Could time really move backwards, with everything coming back to an era of simplicity and ending with a “Big Crunch”? It’s unlikely we’ll be around to find out, but we can postulate on what we think might happen.
另一种理论认为,时间的流逝是由于我们不断膨胀的宇宙。随着宇宙的膨胀,它会带动时间一起前进,因为空间和时间是相互关联的一个整体。但这意味着,如果宇宙达到理论上的膨胀极限并开始收缩,那么时间就会倒流——这是一个小小的悖论。时间真的能倒流吗,一切会回到一个简单的时代,并以 “大挤压” 结束吗?我们不太可能活到那个时候去弄清楚,但我们可以推测一下我们认为可能会发生的事情。
Scientists may not have all the answers, but over the past century they’ve made impressive progress in understanding how time works. From ancient time-telling sundials to modern atomic clocks, we can now track the passing of a second more closely than ever before. Time remains a complex topic, but thanks to scientific visionaries, we are getting closer to unlocking the secrets of this not-so-constant universal constant.
科学家们可能还没有找到所有问题的答案,但在过去的一个世纪里,他们在理解时间的运作方式方面取得了令人瞩目的进展。从古代的计时日晷到现代的原子钟,我们现在能够比以往任何时候都更精确地追踪一秒钟的流逝。时间仍然是一个复杂的话题,但多亏了那些具有科学远见的人,我们正越来越接近解开这个并非那么恒定的宇宙常量的奥秘。
Additional resources and reading
其他资源和阅读材料
To learn more about the concept of time dilation, which we didn’t dive into much here, check out this explainer from the University of Mississippi. There are numerous videos on YouTube that may help you visualize the concept of time and how it works. Here is a great one from the National Institutes of Standards and Technology. Learn more about how time continues to stump even the best physicists in the world in “The Order of Time” by Carlo Rivelli (Riverhead Books, 2018).
要想了解更多关于时间膨胀的概念(我们在这里没有深入探讨这一概念),请查看密西西比大学的这篇解释文章(explainer from the University of Mississippi)。YouTube 上有许多视频可以帮助你形象地理解时间的概念以及它的运作方式。这里有一个来自美国国家标准与技术研究院的很棒的视频(National Institutes of Standards and Technology)。在卡洛·罗韦利(Carlo Rivelli)所著的《时间的秩序》(The Order of Time,Riverhead Books 出版社,2018 年)一书中,你可以了解到时间是如何继续困扰着即使是世界上最优秀的物理学家的。
Bibliography
参考文献
-
Ramsey, Norman F. “History of Atomic Clocks.” Journal of research of the National Bureau of Standards (1977) vol. 88,5 (1983): 301-320. doi:10.6028/jres.088.015
-
Eddington, A. S. (1933). The expanding universe. Nature, 132(3332), 406-407. https://ps.ucw.cz/typeset/eddington.pdf
-
Price, Huw. “Time’s Arrow and Eddington’s Challenge,” Séminaire Poincaré XV Le Temps (2010) 115 – 1
时间单位体系概述
时间单位用于衡量时间的长短,其换算关系基于 10 的幂次,构成了一套有序的体系。在基础时间单位中,秒(s)是国际单位制中的基本时间单位。

一、常见时间单位换算
-
较大时间单位向秒的换算
-
毫秒(ms): 1 ms = 1 0 − 3 s 1 \text{ ms} = 10^{-3} \text{ s} 1 ms=10−3 s,即 1 秒包含 1 0 3 10^{3} 103 个毫秒。例如, 5 ms = 5 × 1 0 − 3 s 5 \text{ ms} = 5 \times 10^{-3} \text{ s} 5 ms=5×10−3 s
-
微秒(μs): 1 μs = 1 0 − 6 s 1 \text{ μs} = 10^{-6} \text{ s} 1 μs=10−6 s,即 1 秒等于 1 0 6 10^{6} 106 微秒。如 30 μs = 30 × 1 0 − 6 s = 3 × 1 0 − 5 s 30 \text{ μs} = 30 \times 10^{-6} \text{ s} = 3 \times 10^{-5} \text{ s} 30 μs=30×10−6 s=3×10−5 s
-
纳秒(ns): 1 ns = 1 0 − 9 s 1 \text{ ns} = 10^{-9} \text{ s} 1 ns=10−9 s,1 秒有 1 0 9 10^{9} 109 纳秒。如 100 ns = 100 × 1 0 − 9 s = 1 0 − 7 s 100 \text{ ns} = 100 \times 10^{-9} \text{ s} = 10^{-7} \text{ s} 100 ns=100×10−9 s=10−7 s
-
皮秒(ps): 1 ps = 1 0 − 12 s 1 \text{ ps} = 10^{-12} \text{ s} 1 ps=10−12 s,表明 1 秒包含 1 0 12 10^{12} 1012 皮秒。如 2000 ps = 2000 × 1 0 − 12 s = 2 × 1 0 − 9 s 2000 \text{ ps} = 2000 \times 10^{-12} \text{ s} = 2 \times 10^{-9} \text{ s} 2000 ps=2000×10−12 s=2×10−9 s
-
-
以表格形式呈现各时间单位换算
| 时间单位 | 符号 | 英文名称 | 与秒的关系 |
|---|---|---|---|
| 秒 | s | Second | 1 s 1 \text{ s} 1 s |
| 毫秒 | ms | Millisecond | 1 0 − 3 s 10^{-3} \text{ s} 10−3 s |
| 微秒 | μs | Microsecond | 1 0 − 6 s 10^{-6} \text{ s} 10−6 s |
| 纳秒 | ns | Nanosecond | 1 0 − 9 s 10^{-9} \text{ s} 10−9 s |
| 皮秒 | ps | Picosecond | 1 0 − 12 s 10^{-12} \text{ s} 10−12 s |
二、时间单位与频率单位关系
时间单位与频率单位紧密相关,二者呈倒数关系。
(一)基础关系公式
频率( f f f,单位 Hz)和时间( T T T,单位 s)的关系为: T = 1 f T = \frac{1}{f} T=f1 ,即完成一次周期性变化所需的时间(周期)等于频率的倒数。
例如,若某交流电频率 f = 50 Hz f = 50 \text{ Hz} f=50 Hz,则其周期 T = 1 50 Hz = 0.02 s T = \frac{1}{50 \text{ Hz}} = 0.02 \text{ s} T=50 Hz1=0.02 s。
(二)频率单位换算
- 1 GHz = 1 0 3 MHz 1 \text{ GHz} = 10^{3} \text{ MHz} 1 GHz=103 MHz
- 1 MHz = 1 0 3 kHz 1 \text{ MHz} = 10^{3} \text{ kHz} 1 MHz=103 kHz
- 1 kHz = 1 0 3 Hz 1 \text{ kHz} = 10^{3} \text{ Hz} 1 kHz=103 Hz
(三)时钟频率与周期换算
-
在计算机及数字电路领域,时钟频率与周期同样遵循上述倒数关系。
以表格展示常见时钟频率对应的周期:
时钟频率( Hz \text{Hz} Hz) 时钟周期( s \text{s} s) 时钟周期( ns \text{ns} ns) 1 Hz 1 \text{ Hz} 1 Hz 1 s 1 \text{ s} 1 s 1 0 9 ns 10^{9} \text{ ns} 109 ns 1 0 3 Hz ( kHz ) 10^{3} \text{ Hz}(\text{kHz}) 103 Hz(kHz) 1 0 − 3 s ( ms ) 10^{-3} \text{ s}(\text{ms}) 10−3 s(ms) 1 0 6 ns 10^{6} \text{ ns} 106 ns 1 0 6 Hz ( MHz ) 10^{6} \text{ Hz}(\text{MHz}) 106 Hz(MHz) 1 0 − 6 s ( μs ) 10^{-6} \text{ s}(\text{μs}) 10−6 s(μs) 1 0 3 ns 10^{3} \text{ ns} 103 ns 1 0 9 Hz ( GHz ) 10^{9} \text{ Hz}(\text{GHz}) 109 Hz(GHz) 1 0 − 9 s ( ns ) 10^{-9} \text{ s}(\text{ns}) 10−9 s(ns) 1 ns 1 \text{ ns} 1 ns -
示例
-
将 1 GHz 1 \text{ GHz} 1 GHz 换算为周期:因为 1 GHz = 1 0 9 Hz 1 \text{ GHz} = 10^{9} \text{ Hz} 1 GHz=109 Hz,根据 T = 1 f T = \frac{1}{f} T=f1,其周期 T = 1 1 0 9 Hz = 1 0 − 9 s = 1 ns T = \frac{1}{10^{9} \text{ Hz}} = 10^{-9} \text{ s} = 1 \text{ ns} T=109 Hz1=10−9 s=1 ns。
-
将 100 ns 100 \text{ ns} 100 ns 换算为频率:先将 100 ns 100 \text{ ns} 100 ns 换算为秒, 100 ns = 100 × 1 0 − 9 s = 1 0 − 7 s 100 \text{ ns} = 100 \times 10^{-9} \text{ s} = 10^{-7} \text{ s} 100 ns=100×10−9 s=10−7 s,再由 f = 1 T f = \frac{1}{T} f=T1,可得频率 f = 1 1 0 − 7 s = 1 0 7 Hz = 10 MHz f = \frac{1}{10^{-7} \text{ s}} = 10^{7} \text{ Hz} = 10 \text{ MHz} f=10−7 s1=107 Hz=10 MHz。
-
(四)常用时钟频率与周期对应表
| 时钟频率( MHz \text{MHz} MHz) | 时钟周期( ns \text{ns} ns) |
|---|---|
| 5 5 5 | 200.00 200.00 200.00 |
| 10 10 10 | 100.00 100.00 100.00 |
| 20 20 20 | 50.00 50.00 50.00 |
| 25 25 25 | 40.00 40.00 40.00 |
| 33 33 33 | 30.30 30.30 30.30 |
| 40 40 40 | 25.00 25.00 25.00 |
| 50 50 50 | 20.00 20.00 20.00 |
| 66 66 66 | 15.15 15.15 15.15 |
| 80 80 80 | 12.50 12.50 12.50 |
| 100 100 100 | 10.00 10.00 10.00 |
| 120 120 120 | 8.33 8.33 8.33 |
| 133 133 133 | 7.52 7.52 7.52 |
| 166 166 166 | 6.02 6.02 6.02 |
| 200 200 200 | 5.00 5.00 5.00 |
| 250 250 250 | 4.00 4.00 4.00 |
| 300 300 300 | 3.33 3.33 3.33 |
| 333 333 333 | 3.00 3.00 3.00 |
| 400 400 400 | 2.50 2.50 2.50 |
| 500 500 500 | 2.00 2.00 2.00 |
| 800 800 800 | 1.25 1.25 1.25 |
| 1000 ( 1 GHz ) 1000 (1 \text{ GHz}) 1000(1 GHz) | 1.00 1.00 1.00 |
| 4000 ( 4 GHz ) 4000 (4 \text{ GHz}) 4000(4 GHz) | 0.25 0.25 0.25 |
(五)时钟周期与频率换算注意事项
-
单位一致性:计算时,时钟频率单位为 Hz,时钟周期单位为 s。若时钟周期以 ns 或 μs 给出,需先转换为 s。
例如,已知时钟周期为 50 ns 50 \text{ ns} 50 ns,计算频率时,先将其转换为 50 × 1 0 − 9 s 50 \times 10^{-9} \text{ s} 50×10−9 s,再代入 f = 1 T f = \frac{1}{T} f=T1 计算。
-
科学计数法应用:由于频率和周期数值常涉及大或小数字,使用科学计数法可简化计算。
如计算 2.5 × 1 0 8 Hz 2.5 \times 10^{8} \text{ Hz} 2.5×108 Hz 的时钟周期, T = 1 2.5 × 1 0 8 Hz = 0.4 × 1 0 − 8 s = 4 × 1 0 − 9 s T = \frac{1}{2.5 \times 10^{8} \text{ Hz}} = 0.4 \times 10^{-8} \text{ s} = 4 \times 10^{-9} \text{ s} T=2.5×108 Hz1=0.4×10−8 s=4×10−9 s。
-
常见单位换算:在计算中频繁使用。
如 1 s = 1 0 9 ns 1 \text{ s} = 10^{9} \text{ ns} 1 s=109 ns, 1 Hz = 1 s − 1 1 \text{ Hz} = 1 \text{ s}^{-1} 1 Hz=1 s−1, 1 MHz = 1 0 6 Hz 1 \text{ MHz} = 10^{6} \text{ Hz} 1 MHz=106 Hz, 1 GHz = 1 0 9 Hz 1 \text{ GHz} = 10^{9} \text{ Hz} 1 GHz=109 Hz ……
三、时间单位应用领域尺度
宇宙学、日常生活、科学研究、微观物理。
1. 朗秒(RonnaSecond,Rs)
1 Rs = 1 0 27 1 \text{ Rs} = 10^{27} 1 Rs=1027 秒
在宇宙学中,当研究宇宙的演化历史、星系的形成与演化等极其漫长的时间过程时,可能会用到朗秒这样的大时间单位来进行量级上的描述。不过,由于宇宙的年龄目前估计约为 138 亿年,换算成秒约为 4.35 × 1 0 17 4.35 \times 10^{17} 4.35×1017 秒,与朗秒相比仍然小很多数量级,所以在实际的宇宙学研究中,朗秒也并不经常直接使用,更多是作为一种理论上的大时间尺度参考。
2. 约塔秒(Yottasecond,Ys)
1 Ys = 1 0 24 1 \text{ Ys} = 10^{24} 1 Ys=1024 秒
在一些理论物理模型中,对于涉及到宇宙极早期或者极其漫长的时间跨度的理论探讨时,约塔秒可能会被提及。但在实际的科学研究和日常应用中,由于其表示的时间跨度实在太大,很少有具体的现象或过程能直接用约塔秒来精确度量。从宇宙大爆炸至今的时间与约塔秒相比,显得极其微小。
3. 泽秒(Zettasecond,Zs)
1 Zs = 1 0 21 1 \text{ Zs} = 10^{21} 1 Zs=1021 秒
在宇宙学等领域,当研究宇宙的演化、星系的形成和发展等极其漫长的过程时,可能会用到泽秒这样的时间单位来进行大致的量级估算和描述。例如,宇宙从大爆炸开始到现在的时间大约为 4.35 × 1 0 17 4.35 \times 10^{17} 4.35×1017 秒,用泽秒来衡量的话,大约是 0.000435 0.000435 0.000435 泽秒。
4. 艾秒(Exasecond,Es)
1 Es = 1 0 18 1 \text{ Es} = 10^{18} 1 Es=1018 秒
在一些涉及到宇宙中极为漫长时间跨度的研究中,可能会用到艾秒这个时间单位,但在实际应用中相对较少。
5. 拍秒(PetaSecond,Ps)
1 Ps = 1 0 15 1 \text{ Ps} = 10^{15} 1 Ps=1015 秒
在天文学等领域可能会用到,比如研究星系演化等一些极其缓慢的宇宙过程可能会涉及到拍秒量级的时间。
6. 太秒(Terasecond,Ts)
1 Ts = 1 0 12 1 \text{ Ts} = 10^{12} 1 Ts=1012 秒
在一些较长时间跨度的科学研究或特定的理论计算中可能会使用太秒作为时间单位。
7. 吉秒(Gigasecond,Gs)
1 Gs = 1 0 9 1 \text{ Gs} = 10^{9} 1 Gs=109 秒
吉秒在一些涉及到较长时间周期的科学研究或工程计算中可能会用到。
8. 兆秒(Megasecond,Ms)
1 Ms = 1 0 6 1 \text{ Ms} = 10^{6} 1 Ms=106 秒
兆秒在一些需要度量较长时间但又不需要太大数量级的情况下可能会被使用。
9. 千秒(Kilosecond,ks)
1 ks = 1 0 3 1 \text{ ks} = 10^{3} 1 ks=103 秒
千秒在一些时间度量中可以作为一个中间量级的单位,例如在一些工业生产流程或特定的实验记录中可能会用到。
10. 百秒(Hectosecond,hs)
1 hs = 1 0 2 1 \text{ hs} = 10^{2} 1 hs=102 秒
百秒在一些较短时间范围的计量中可以作为一个合适的单位,例如在一些体育比赛的部分环节计时中可能会使用。
11. 十秒(Dekasecond,das)
1 das = 10 1 \text{ das} = 10 1 das=10 秒
十秒在一些简单的时间计量场景中,如一些简单的倒计时或短时间的活动计时中可能会用到。
12. 秒(Second, s)
时间的基本单位,是国际单位制中七个基本单位之一。
日常生活中的大多数时间计量都以秒为基础,比如时钟的滴答声,每一秒就是一个基本的时间间隔。
13. 分秒(Decisecond,ds)
1 ds = 1 0 − 1 1 \text{ ds} = 10^{-1} 1 ds=10−1 秒
分秒在一些需要更精确时间计量且时间尺度相对较短的情况下可能会用到,例如在一些高精度的实验测量或特定的计时设备中。
14. 厘秒(Centisecond,cs)
1 cs = 1 0 − 2 1 \text{ cs} = 10^{-2} 1 cs=10−2 秒
厘秒在一些对时间精度要求较高的科学实验或技术应用中可能会用到,比如在一些精密机械的运动控制或高精度的时间测量设备中。
15. 毫秒(Millisecond, ms)
1 ms = 1 0 − 3 1 \text{ ms} = 10^{-3} 1 ms=10−3 秒
常用于计算机程序的运行时间、体育比赛中的成绩记录等,如短跑比赛中运动员的成绩可能精确到毫秒。
16. 微秒(Microsecond, μ \mu μs)
1 μ s = 1 0 − 6 1 \text{ } \mu\text{s} = 10^{-6} 1 μs=10−6 秒
在电子电路、通信等领域有广泛应用,比如电子信号的传输延迟等可能会以微秒来计量。 注意,这里在μ和s之间添加一个空格,使渲染更正确。
17. 纳秒(Nanosecond, ns)
1 ns = 1 0 − 9 1 \text{ ns} = 10^{-9} 1 ns=10−9 秒
在高速电子器件、半导体物理等领域非常重要,例如芯片内部的信号传输和处理时间常常在纳秒量级。
18. 皮秒(PicoSecond, ps)
1 ps = 1 0 − 12 1 \text{ ps} = 10^{-12} 1 ps=10−12 秒
常用于描述极短的时间过程,比如在激光技术中,一些超短脉冲激光的脉冲宽度可以达到皮秒量级,用于材料加工、生物成像等领域。
19. 飞秒(Femtosecond, fs)
1 fs = 1 0 − 15 1 \text{ fs} = 10^{-15} 1 fs=10−15 秒
常用于超快光学、化学反应动力学等领域,用于研究分子和原子在化学反应中的快速过程。
20. 阿秒(Attosecond, as)
1 as = 1 0 − 18 1 \text{ as} = 10^{-18} 1 as=10−18 秒
主要用于研究原子和分子内部的超快过程,如电子在原子内部的运动等。
21. 仄秒(ZeptoSecond, zs)
1 zs = 1 0 − 21 1 \text{ zs} = 10^{-21} 1 zs=10−21 秒
在研究原子核内部的一些超快现象以及超高能物理过程等方面有重要意义,不过由于时间尺度极短,相关研究相对较为前沿和困难。
22. 约秒(Yoctosecond,ys)
1 ys = 1 0 − 24 1 \text{ ys} = 10^{-24} 1 ys=10−24 秒
约秒在一些极微观的物理理论研究中,如对一些基本粒子相互作用的极短时间过程的探讨中可能会涉及到,但在实际应用中非常罕见。
23. 朗托秒(RontoSecond, Rs)
1 Rs = 1 0 − 27 1 \text{ Rs} = 10^{-27} 1 Rs=10−27 秒
在极微观的物理过程研究,如某些超高能粒子相互作用的极短时间尺度模拟,或者在理论物理中对一些极端条件下的时空模型进行理论推导时,可能会涉及到朗托秒这样极小的时间单位。但由于其量级极小,目前在实际应用中相对较少,更多是在前沿科学的理论探索领域。
24. 奎达秒(QuectoSecond, Qs)
1 Qs = 1 0 − 30 1 \text{ Qs} = 10^{-30} 1 Qs=10−30 秒
在一些极端的物理现象模拟,如对大爆炸最初期的瞬间物理过程进行理论建模,或者在研究一些目前尚未完全探测到的极短寿命粒子的衰变过程等方面,奎达秒可能会作为理论上的时间尺度来使用。它处于目前人类对时间尺度认知的极微观边缘,更多地存在于理论物理的前沿研究中。
25. 普朗克时间(Planck Time, t P t_{\mathrm{P}} tP)
t P ≈ 5.39 × 10 − 44 t_{\mathrm{P}} \approx 5.39\times {{10}^{-44}} tP≈5.39×10−44 秒
t P t_{\mathrm{P}} tP 是时间的最小可测单位,被认为在这个尺度下现有的物理理论可能会发生重大变革。
普朗克时间为
t P = ℏ G c 5 s \begin{align*} {{t}_{\mathrm{P}}}= & \sqrt{\frac{\hbar G}{{{c}^{5}}}} \text{s} \end{align*} tP=c5ℏGs
其中, c c c 为真空中光速, G G G 为万有引力常数(引力常量), G = 6.67259 × 1 0 − 11 N ⋅ m 2 / k g 2 G = 6.67259\times10^{-11}\mathrm{N\cdot m^{2}/kg^{2}} G=6.67259×10−11N⋅m2/kg2, ℏ \hbar ℏ 是约化普朗克常数或称狄拉克常数,记为 ℏ = h 2 π \hbar=\frac{h}{2\pi} ℏ=2πh, h h h 为普朗克常数,用以描述量子大小,它在量子力学中占有重要的角色。马克斯·普朗克在 1900 年研究物体热辐射的规律时发现,只有假定电磁波的发射和吸收不是连续的,而是一份一份地进行的,计算的结果才能和试验结果是相符。这样的一份能量叫做能量子,每一份能量子等于 h ν h\nu hν, ν \nu ν 为辐射电磁波的频率。
时间的数量级例解
时间的数量级(order of magnitude of time)通常是一个十进制前缀或十进制数量级的量,再加上一个时间的基本单位。前者如“微秒”(microsecond),后者如“百万年”(million years)。
在某些情况下,数量级可能是隐含的(通常为 1),如“秒”或“年”;在其他情况下,量的名称暗示其基本单位,如“世纪”;在大多数情况下,基本单位是“秒”或“年”。
下面按时间长短列出一些例子,以帮助理解不同时间长度的概念,比较时间单位的数量级。
普朗克时间:约 5.39 × 1 0 − 44 5.39 \times 10^{-44} 5.39×10−44 秒
普朗克时间是光波在真空中传播一个普朗克长度的距离所需的时间。理论而言,它是最小的可测时间间隔。在这短暂时间间隔里所发生的任何变化无法经测量或探测求得。
幺秒(ys): 1 0 − 24 10^{-24} 10−24 秒
1 幺秒(yoctosecond)约是 1.86 × 1 0 19 1.86 \times 10^{19} 1.86×1019 普朗克时间。
- 0.3 幺秒 – W 和 Z 玻色子平均寿命
- 156 幺秒 – 希格斯玻色子寿命
仄秒(zs): 1 0 − 21 10^{-21} 10−21 秒
1 仄秒(zeptosecond)即 1000 幺秒。
- 1 仄秒 – 放射性原子核衰变释放伽马射线的典型周期时间(这里为激发光子能量是 2 MeV)
阿秒(as): 1 0 − 18 10^{-18} 10−18 秒
阿秒(attosecond)是目前实验上能测量的最小时间尺度,等于 1 0 − 18 10^{-18} 10−18 秒,又称原秒。
- 150 阿秒 – 当氢原子核外电子处于基态时,电子绕原子核运动一周需要约 150 阿秒。
飞秒(fs): 1 0 − 15 10^{-15} 10−15 秒
飞秒(femtosecond)为千万亿分之一秒, 1 0 − 15 10^{-15} 10−15 秒。
- 1 飞秒 – 光在真空中传播 0.3 微米的时间。
- 1.30 到 2.57 飞秒 – 可见光的振荡周期。
皮秒(ps): 1 0 − 12 10^{-12} 10−12 秒
1 皮秒(picosecond)即 1000 飞秒。
纳秒(ns): 1 0 − 9 10^{-9} 10−9 秒
1 纳秒(nanosecond)即 1000 皮秒,也叫纳秒、奈秒、诺秒、纤秒、那诺秒、毫微秒。
- 1 纳秒 – 1 GHz 的 CPU 的时钟周期,该周期的无线电波波长 0.3 米。
- 3.3 纳秒 – 光传播一米所需的时间。
- 10.9 纳秒 – 铯 133 原子基态的超精细能级跃迁周期的大致长度,这个周期被用来定义秒的长度。
- 10 纳秒 – 该周期的无线电波波长 3 米(VHF、FM 波段)。
- 12 纳秒 – K 介子的半衰期。
- 100 纳秒 – 短波周期。
- 300 纳秒 – 钫 - 233 的半衰期。
微秒(µs): 1 0 − 6 10^{-6} 10−6 秒
1 微秒(microsecond)即 1000 纳秒。
- 1 微秒 – 商业高速频闪观测器的闪动时间。
- 22.7 微秒 – CD 音乐的采样间隔(44.1 kHz)。
- 50 微秒 – 人能够听到的最高频率声音的周期(20 kHz)。
- 125 微秒 – 电话声音的采样间隔(8 kHz)。
毫秒(ms): 1 0 − 3 10^{-3} 10−3 秒
1 毫秒(millisecond)即 1000 微秒。
- 1 毫秒 – 大部分电脑计算时间的基本单位,许多程序计算延迟的基本单位。
- 2.4 毫秒 – 鿔元素的半衰期。
- 3 毫秒 – 苍蝇扇一次翅膀的时间。
- 5 毫秒 – 蜜蜂扇一次翅膀的时间。
秒(s)
国际单位制中时间的基本单位,本页面的单位基准。1 秒即 1000 毫秒。
一般很少使用比秒更大的字头单位(如千秒等),而用小时、日、年等。
- 60 秒 – 1 分钟的长度。
千秒(ks): 1 0 3 10^{3} 103 秒
1 千秒(kilosecond)即 1000 秒,相当于 16 分钟 40 秒,或 16 2 3 16 \frac{2}{3} 1632 分钟。
- 3.6 千秒 – 即 3600 秒,1 小时的长度。
- 86.4 千秒 – 即 86400 秒,1 日的长度。
兆秒(Ms): 1 0 6 10^{6} 106 秒
1 兆秒(megasecond)即 1000 千秒,相当于约 11.57 天,或 277 小时 46 分钟 40 秒。
- 2.592 兆秒 – 30 天的长度;这相当于格里历的 1 个小月。
吉秒(Gs): 1 0 9 10^{9} 109 秒
1 吉秒(gigasecond)等于 1,000,000,000 秒,大概等于 31.7 年。
太秒(Ts): 1 0 12 10^{12} 1012 秒
1 0 13 10^{13} 1013 秒
相当于 32 万年。
- 34 万年 - 核素锔 - 248 的半衰期。
- 约 60 万年前 - 人类语言发音成型。
- 约 70 万年前 - 地球磁场对上一次顺逆转。
- 100 万年 - 蓝超巨星的生命周期。
- 153 万年 - 核素锆 - 93 的半衰期。
- 258.8 万年 - 地球的第三纪终结,第四纪开始的纪元距今时间。
- 260 万年 - 核素锝 - 97 的半衰期。
1 0 14 10^{14} 1014 秒
相当于 317 万年。
- 374 万年 - 核素锰 - 53 的半衰期。
- 400 万年 - 物种的估计生命周期。
- 400 万年 - 最后一个冰河时期开始的距今时间。
- 420 万年 - 核素锝 - 98 的半衰期。
- 500 万年 - 中新世终结,上新世开始的纪元距今时间。
- 650 万年 - 核素钯 - 107 的半衰期。
- 1560 万年 - 核素锔 - 247 的半衰期。
- 2000 万年 - 原始草在地球出现的距今时间。
- 2342 万年 - 核素铀 - 236 的半衰期。
- 2400 万年 - 渐新世终结,中新世开始的纪元距今时间。
1 0 15 10^{15} 1015 秒(拍秒,Ps)
相当于 3200 万年。
- 3,470 万年 - 核素铌 - 92 的半衰期。
- 3,600 万年 - 始新世终结,渐新世开始的纪元距今时间。
- 4,000 万年 - 预计在未来,大洋洲大陆撞击亚洲大陆所需时间。
- 6,500 万年 - 地球上一次生物大灭绝的距今时间。
- 1.35 亿年 - 侏罗纪终结,白垩纪开始的距今时间。
- 1.95 亿年 - 三叠纪终结,侏罗纪开始的距今时间。
- 2.25 亿年 - 二叠纪终结,三叠纪开始的距今时间。
- 2.26 亿年 - 太阳系绕银河系中心公转一周的所需时间。
- 2.80 亿年 - 石炭纪终结,二叠纪开始的距今时间。
1 0 16 10^{16} 1016 秒
相当于 3.2 亿年。
- 3.40 亿年 - 泥盆纪终结,石炭纪开始的距今时间。
- 4.00 亿年 - 志留纪终结,泥盆纪开始的距今时间。
- 4.20 亿年 - 首只动物呼吸空气的距今时间。
- 4.35 亿年 - 奥陶纪终结,志留纪开始的距今时间。
- 5.00 亿年 - 寒武纪终结,奥陶纪开始的距今时间。
- 5.40 亿年 - 前寒武纪终结,寒武纪开始的距今时间。
- 5.80 亿年 - 雪球地球冰河时代终结的距今时间。
- 6.00 亿年 - 第一代多细胞生命出现的距今时间。
- 7.038 亿年 - 核素铀 - 235 的半衰期。
- 7.50 亿年 - 雪球地球冰河时代开始的距今时间。
- 12.77 亿年 - 核素钾 - 40 的半衰期。
- 23.00 亿年 - 首个已知冰河时代的距今时间。
1 0 17 10^{17} 1017 秒
相当于 32 亿年。
- 35 亿年 - 原核生物出现的距今时间。
- 37 - 39 亿年 - 月球表面雨海的年龄。
- 44.68 亿年 - 核素铀 - 238 的半衰期。
- 45 亿年 - 地球的年龄。
- 100 亿年 - 类似太阳主序星(G2 型)的平均寿命。
- 137.99 ± 0.21 亿年 - 根据大爆炸理论,宇宙的估计年龄。
1 0 18 10^{18} 1018 秒(Es)
相当于 320 亿年。
- 1000 亿年 - 宇宙的寿命(假设宇宙是封闭的)。
- 2922 亿 7702 万 6596 年又 12 个月 4 日 15 小时 30 分 08 秒 - 64 位系统下,UNIX 时间最多可以表示到的时间点。
1 0 19 10^{19} 1019 秒以上
相当于 3,200 亿年以上的时间。
注:此处“兆”为“万亿”;“京”为“亿亿”。
- 5845 亿 5405 万 3193 年又 10 个月 7 天 7 小时零 16 秒 - 64 位系统下,UNIX 纪年总共可覆盖的时间长度。
- 311 兆年 - 印度教梵天的寿命。
- 8000 兆年 - 核素镉 - 113 的半衰期。
- 8000 兆年 - (M 型)型红矮星的寿命。
- 27 京年 - 核素钒 - 50 的半衰期。
- 1900 ± 200 京年。
……
时间统一系统
在航天活动中,各测控站所获取、记录的测量数据和事件都必须有严格统一的时间标准,才能对它们进行分析和处理,使其具有使用价值。时间信号还用于控制程序仪器,完成火箭、导弹的点火以及使仪器按程序工作。
定义
时间统一系统是为测控系统提供统一标准时间信号和标准频率信号的系统。航天测控设备种类多、数量大、分布广,如果没有统一的时间长度,根本无法完成任务。发射起飞时间 ( L L L)、各级火箭发动机的点火与关机时间、分离时间、数据注入时间、星 (船) 箭分离时间、航天器入轨时间等关键事件特征点,都需要时统系统提供准确的时刻。时间统一系统连续可靠、稳定的运行是测控系统正常工作的前提,其性能优劣直接影响航天测控系统的测量精度和测量体制。典型的时间统一系统组成如图 1 所示。它由时间频率基准及发播系统、定时校频信号接收系统、本地频率标准、时间码产生器、分配放大器和用户设备等组成。 [1] img
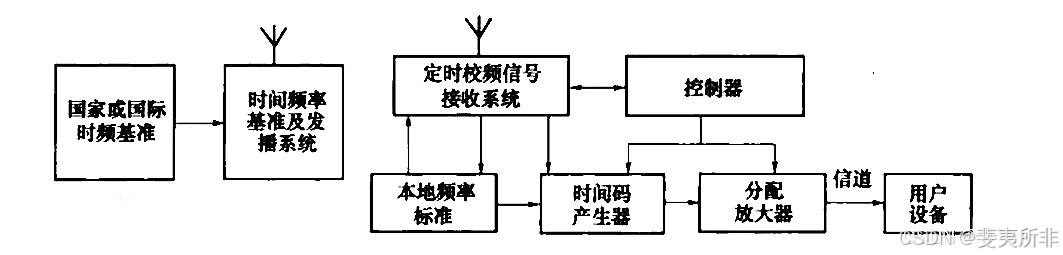
基准
时间基准
世界各国以性能优异的原子钟建立并保持着本国的时间体系。GPS 时间是美国的一种时间基准,GLONASS 是俄罗斯的一种时间基准,北京时是我国的主要时间基准。各国的时间基准通过协调世界时 (UTC) 可以互相比较,因而误差很小,对航天测控系统的测量精度影响可以忽略。因此,时间统一系统广泛采用多个时间基准互为备份,择优使用。 [1]
频率标准
时间统一系统应用的频率标准有 3 类。
第一类是铯原子频标和氢原子频标。
铯原子频标的长期频率准确度极高,常用的是商业型铯原子频标,频率稳定度在 1 0 − 11 s 10^{-11}\ s 10−11 s 量级,准确度在 1 0 − 14 s 10^{-14}\ s 10−14 s 量级。氢原子频标的特点是既具有很高的频率准确度,又有很高的频率稳定度 (小于 1 × 1 0 − 12 s 1×10^{-12}\ s 1×10−12 s),而且已实现国产化。氢原子频标按工作原理分为被动型和主动型。被动型氢原子频标体积小,频率准确度在 1 0 − 12 s 10^{-12}\ s 10−12 s 量级;主动型氢原子频标体积大,频率准确度在 1 0 − 13 s 10^{-13}\ s 10−13 s 量级,甚至更高。
第二类是铷原子频标。
按工作原理分为抽运型和激射型,后者较前者短期频率稳定度高。常用的是较为经济的抽运型铷原子频标,频率准确度在 1 0 − 10 s 10^{-10}\ s 10−10 s 量级,频率稳定度在 1 0 − 11 s 10^{-11}\ s 10−11 s 量级。铷原子频标由于技术成熟,性能价格比高、小型化及工程化程度高等特点,已大量应用于航天测控系统,成为标准化时统设备的重要组成部分。
第三类是石英晶体频标。
它是以石英晶体压电效应产生的稳定振荡信号为频率标准。普通石英晶体振荡器的频率准确度为 1 0 − 5 ~ 1 0 − 6 s 10^{-5}~10^{-6}\ s 10−5~10−6 s,温度补偿石英晶体振荡器的频率准确度为 1 0 − 6 ~ 1 0 − 7 s 10^{-6}~10^{-7}\ s 10−6~10−7 s,恒温型石英晶体振荡器的频率准确度为 1 0 − 8 ~ 1 0 − 9 s 10^{-8}~10^{-9}\ s 10−8~10−9 s。石英晶体振荡器的频率稳定度为 1 0 − 10 ~ 1 0 − 12 s 10^{-10}~10^{-12}\ s 10−10~10−12 s。石英晶体频标体积小、频率稳定度较高,但开机需要预热,达到指标需要几十分钟甚至几十小时,受环境温度影响大,频率准确度需要定期校准。
标准时统
标准化的时统设备由定时校频单元、频标单元、时码产生单元、时码区分单元、监控计算机等组成。定时校频单元一般具有 GPS 和长短波授时系统定时校频手段;频标单元由铷原子频标和通用石英频标组成本地冗余的频率标准;时码产生单元通过 3 个以上的冗余模块形成标准格式的 B 时间码,经过时码区分单元分配传输给附近的用户设备;监控微机直观显示各单元参数、状态,向上级网管报告设备运行情况。
标准化时统设备具有时差测量、延迟修正、闰秒、闰年、时间设置、故障告警等功能,可靠性与稳定性较高,分布于各大型测控站,为测控设备提供统一标准的时频信号格式。
时频信号发播
时频信号发播系统将时间基准传递或传输到远距离的用户,解决覆盖范围和同步精度问题,多采用无线电波传送方式。航天测控系统应用的时频信号发播系统有美国 GPS、俄罗斯 GLONASS、我国北斗定位系统以及长波授时系统和短波授时系统 (BPM) 等。
利用卫星传递或发播定时信号是一种覆盖面宽、精度高的定时手段。其中典型的为美国 GPS (定时系统),利用它的精码可达 10 ns 量级的定时精度,粗码亦可达 100 ns 量级的定时精度。北斗定位系统是我国建立的区域卫星定位试验系统,仅地面设有原子钟组,定时性能低于 GPS,应用普及程度较低。长波授时系统和短波授时系统的电波传输主要依靠电离层的反射进行,是一种服务面宽而价格又低廉的手段,但由于电离层的不稳定性,其信号质量相对 GPS 较差。我国的短波授时、长波授时系统由陕西临潼的国家授时中心维持和发播。 [1]
定时校频方法
通过时频发播系统 (或其他信道) 完成本地时统设备与上级时间基准的时间同步和频率校准,简称定时与校频,是时统设备一项关键性工作。定时校频方法一般根据工程任务需要、现有技术设备条件和应用环境条件来综合确定。
定时方法分为卫星单向定时、长短波定时、双向定时等。
卫星单向定时是从接收的导航定位卫星信号中提取时频信号,补偿电离层、传播路径等各种延迟,完成本地时间信号的输出。常用技术有 GPS 单向定时、北斗单向定时、GPS/GLONASS 组合单向定时、GPS / 北斗组合单向定时、GPS/GIDNASS/ 北斗组合单向定时。定时精度范围在 1 0 − 6 ~ 1 0 − 8 s 10^{-6}~10^{-8}\ s 10−6~10−8 s。
长短波定时是接收我国授时中心或其他授时台发播的长波、短波信号,补偿电离层、传播路径等各种延迟,完成本地时间信号的输出。常用技术有短波授时系统单向定时,定时精度在 1 0 − 3 s 10^{-3}\ s 10−3 s 量级;长波授时系统单向定时,定时精度在 1 0 − 6 s 10^{-6}\ s 10−6 s 量级。
双向定时是两地的时统设备通过专用信道 (卫星、光纤等) 互相发送接收时频信号,彼此交换测量数据,修正本地时间基准,从而实现两地间的时间统一。双向定时精度较高,一般在 1 0 − 8 ~ 1 0 − 10 s 10^{-8}~10^{-10}\ s 10−8~10−10 s 范围。
校频方法与定时方法密不可分,校频的主要工作是测量频率标准与被测设备的频差等参数,然后予以调整。频差往往通过测量周期时间内二者的相位变化量来获取。 [1]
具体应用
在航天活动中,各测控站所获取、记录的测量数据和事件都必须有严格统一的时间标准,才能对它们进行分析和处理,使其具有使用价值。时间信号还用于控制程序仪器,完成火箭、导弹的点火以及使仪器按程序工作。航天器发射场、航天测控站中都配有时间统一系统,用以使各种测量设备同步工作,保证航天活动正常进行。现代航天时间同步精度已从毫秒量级达到纳秒(毫微秒)量级。
时间统一系统由时统中心和若干时统分中心组成,其设备由无线电接收机、原子频率标准、标准信号发生器和放大分配设备组成。接收机接收国家天文台播发的标准时间和标准频率信号,使各时统系统与标准时间和标准频率保持同步。
频率标准源产生准确而稳定的基准信号,送至信号和时间发生器,经分频和综合形成各种频率的标准信号、采样信号、控制信号和时间码等信号,由分配设备放大后,经有线电缆或无线电线路送给用户设备。航天工程中常用高稳定恒温晶体振荡器和原子频率标准作为标准频率源。用户设备与时统中心的距离不同,时统信号到达各设备的时间延迟也有差异,当要求精确同步时,必须测出这些信号的传输时延,在数据处理过程中加以修正。
航天活动中常用的标准时间有 3 种:
① 世界时 (UT):以地球自转为基础的时间计量系统,由于地球自转速度变化的影响,这种时间的刻度是不均匀的。
② 原子时 (AT):以原子共振现象所产生的恒定频率为基准而建立的时间计量系统,它的时间刻度十分均匀。
③ 协调世界时 (UTC): 以原子时秒长为基础,时刻尽量接近于世界时的一种时间计量系统。协调世界时秒长严格等于原子时秒长,起点与世界时基本一致,用跳秒办法使其与世界时的刻度差总小于 0.9 秒。这样既能保持时间刻度的高度均匀,又能使它与地球自转密切相关。[2]
发展方向
从静态到动态
以往的时统设备无论是固定站使用的还是车载或船载的,在使用时都是静态的。因此这些车载或船载时统设备只是属于可搬动式的设备,它们的工作状态与固定台站使用的设备差别不大,所需注意的仅是防止运动过程对设备的损坏。随着导弹机动作战能力的提高,对这类飞行器测量的机动要求必然会随之提出。因此需要时统设备能适应动态工作条件,如能在车载或机载的工作环境下可靠地工作。对航天器的测量正在由陆基向天基发展,如用跟踪与数据中继卫星实现对中、低轨道航天器的测控,因此这类卫星上的时统设备就应能适应在星载条件下工作。
动态条件下工作的时统设备主要需解决下述 2 方面的问题。
(1) 设备不仅应能经得住恶劣的运输环境的考验,还需在动态的环境下工作。诸如环境温度的剧烈变化、振动、冲击、过载和辐射等环境条件都会对时统设备的工作造成影响,其中频率标准对工作环境的变化最为敏感。因此在动态条件下工作的时统设备在研制时要注意解决恶劣环境对设备工作的影响。此外在使用中应为时统设备创造尽可能好的工作环境,如采取恒温、减震等措施以减轻环境条件变化对设备工作的影响。
(2) 由于时统设备处于动态的工作环境,其空间位置在不断变化,给需要精确空间位置来计算电波传播时延的定时设备的工作带来困难。因为空间位置的不断变化意味着从授时台到定时设备的电波时延也在不断变化。对此需根据对时间同步误差的要求和空间位置变化的速率,选用或研制相应的高动态定时设备以满足时统设备时间同步工作的需要。
纳秒量级时间
一种新的测量体制要求相距几十千米的站间时间同步误差达到纳秒量级。如果站间的时间同步能达到纳秒量级,几个站同时接收来自飞行器的信号就可精确测量其位置。这种测量体制会使原本较难实现的多目标跟踪测量迎刃而解,因为只需在每个目标内装有可区分的信标就可解决对多目标的测量。如果测量站是可移动的,还可很方便地用于不同地方的无线电测量设备的精度鉴定工作。这将使通常用精密的光学测量系统靠校飞的方法来进行的精度鉴定工作大为简化。
纳秒量级时间同步的实现首先要解决的是高精度定时手段。激光可以用来传递高精度的时间信号,但由于测量站均在地面,要实现几十千米激光的传输需要建高塔,而且激光的传输受气候条件如雨、雪等的影响很大。 [3]
参考资料
- 崔吉俊主编,航天发射试验工程,中国宇航出版社,2010.12
- 探访北京飞控中心 “时间统一系统”.科技网 - 数字报.2013-12-03 [引用日期 2015-11-2]
- 中国人民解放军总装务部军事训练教材编辑工作委员会编,时间统一技术,国防工业出版社,2004 年 07 月第 1 版
时间统一系统授时方式简介
作者:西安同步电子小康
发布于:2019 - 04 - 14 18:04
在通信业务高速发展与通信网络规模不断扩大的时代,通讯设备类型日益增多,不同类型的通讯产品要求能在同一个网管平台上做到统一管理的需求不断显现。统一网管运行需要时间统一系统提供时钟系统级的服务,时钟系统服务成为一个重要的研究领域。
网络时间服务的实现方式
时间服务器:可使用时钟同步服务器来同步网络中各个终端的时钟时间。所有客户终端从该同步时钟服务器获取标准时间,且无需与局域网外的系统进行时钟同步。同时,由于某些原因不能使用无线时钟,这种方式成为最佳选择。
网络时间服务的工作模式
1.主 / 被动对称模式:双方均可同步对方或被对方同步,可理解为一方作为服务器,另一方作为客户端。先发出申请建立连接的一方工作在主动模式下,另一方工作在被动模式下。
2.客户 / 服务器模式:与主 / 被动模式基本相同,唯一区别在于客户方可被服务器同步,但服务器不能被客户同步。
3.广播模式:这是一种一对多的连接方式。服务器不管客户终端处于何种状态,主动发出时间信息,客户终端据此调整本地时间。此模式忽略网络延时,在精度上有损失,但可满足秒级应用。
时间信息的传输大多使用 NTP 协议。每个时间包包含最近一次事件的时间信息,如上次事件的发送与接收时间、传递现在事件的当地时间及此包的接收时间。收到时间包后,即可估算出时间的延迟及偏差量。
时钟同步的主要功能
1.时钟同步功能:系统根据时钟同步方式(手工和定时)调整操作系统时间和系统维护的时钟源信息,使系统内部各个节点的时钟与时钟源服务器保持一致。任意一个时钟同步客户端发起时钟同步消息,时钟同步的服务器端返回系统时钟信息,客户端根据时钟信息调整操作系统时间和系统维护的时钟源信息。同时,时钟同步的服务器端定时和时钟源服务器进行时钟同步。
2.时钟获取功能:系统向应用或用户提供一个准确的、与操作系统和硬件时钟运行时无关的时钟信息。当操作系统时间被修改时,应用或用户获取到的时钟信息不受影响。
3.时钟检查功能:能自动检查系统维护的本地时钟源和时钟同步服务器之间的误差,当达到预设的阈值时能够进行时钟告警,同时向消息服务器的主题发送一个告警信息。
时钟同步的时间误差和时钟源服务器之间的误差保持在秒一级。由于在网管系统中,每一级所带的客户端可能不止一台,当同时有多个客户端进行时钟同步时,服务器端应能处理多个客户的请求。
高可靠、高精度的时间统一系统体系涉及守时系统、授时系统、授时监测发播系统、时频终端设备、时统保障系统等多个方面。通过完备的时间产生、发播、监测和服务体系,为用户提供高可用性、统一的时间频率服务。守时系统的基本任务是通过高精度原子钟组及测量、比对与处理设备建立和保持一个高准确度、高稳定性的标准时间基准,并提供可靠、连续实时的时间和频率信号。授时系统的基本任务是通过有线或无线手段将守时系统保持的标准时间传递给用户。授时监测发播系统的作用是对授时系统所发播信号进行监测,确保用户获取标准时间的精度和可靠性。时频终端设备的基本任务是接收和保持标准时间,并向用户提供连续可靠的标准时间和频率信号。时统保障系统是对时间服务制定法规和标准,并对各类时频装备进行计量校准,确保各类时频装备处于正常状态。
授时系统
守时系统产生和保持的标准时间基准,需要通过各种授时系统将基准时间频率传送到用户端使用。目前可用的授时系统包括卫星导航授时系统、长波授时系统、短波授时系统、网络授时、电视授时、电话授时等,也可根据特殊需要自建授时系统。
1.卫星导航授时系统
世界上主要的卫星导航授时系统有美国的 GPS、俄罗斯的 GLONASS、欧洲的 Galileo 和我国的北斗卫星导航授时系统。卫星授时系统可提供 10 纳秒级的授时精度。
-
GPS 系统时间:GPS 卫星系统时间 GPST 为连续的时间尺度,其溯源到美国海军天文台的协调世界时 UTC。
-
GLONASS 系统时间:俄罗斯的 GLONASS 时间采用 UTC 作为时间参考。
-
Galileo 系统时间:伽利略(Galileo)是欧洲在建的全球卫星导航定位系统,其时间参考系统 GTS 正在考虑其时间起点是否与 GPS 接轨,即也采用与 TAI 在整数秒上相差 19s。GST 将被驾驭到一种时间预报上,这一预报通过 Galileo 时间供应商从欧洲的几个主要守时实验室获得。
-
北斗系统时间:北斗系统时间是由北斗二代地面运控系统主控站时频系统建立并保持的时间,简称 BDT。BDT 采用国际原子时秒长(SI)为基本单位,以 “周” 和 “周内秒” 为单位连续计数,通过北斗导航电文发播;BDT 不闰秒,时间历元起点为 2006 年 1 月 1 日。
2.长波授时系统
长波授时系统有罗兰 C 授时(中科院的长波授时台(代号:BPL)属于罗兰 C 体制)、低频时码(代号:BPC)等。罗兰 C 授时精度可优于 1μs,低频时码授时精度为 0.5ms。
结束语
时间作为国际单位制的 7 个基本单位之一,是目前可以实现测量的精度最高的一个量。时间相关技术的发展,促进了其它领域的技术进步。现代科技的发展和进步,也极大地提高了时间频率技术的性能。时间和频率作为常用的基本参量,对人类日常生活和工作有重要影响。随着社会的发展,将需要更高准确度的时间基准和更精密的时间测量技术,开展时间相关领域的研究对促进科技进步具有重要意义。
1 秒的百亿亿分之一:诺贝尔物理学奖授予三位阿秒激光科学家
2023-10-03 21:39
知世 发布于:北京市
2023 年 10 月 3 日,瑞典皇家科学院宣布,将 2023 年诺贝尔物理学奖授予美国俄亥俄州立大学名誉教授皮埃尔・阿戈斯蒂尼(Pierre Agostini)、德国马克斯・普朗克量子光学研究所教授费伦茨・克劳斯(Ferenc Krausz)和瑞典隆德大学教授安妮・卢利尔(Anne L’Huillier),以表彰他们在 “产生阿秒光脉冲以研究物质中电子动力学的实验方法” 方面所做出的贡献。

三人将平分 1100 万瑞典克朗(约合 732 万元人民币)的奖金。安妮・卢利尔也成为第 5 位获得诺贝尔物理学奖的女性。
值得一提的是,此次得奖的三人中,有两人获得了去年的沃尔夫奖(Wolf Prize),该奖项也被称为诺贝尔奖的风向标。
评委会在发布的一份新闻声明中表示,三位 2023 年诺贝尔物理学奖获得者所进行的实验为人类探索原子和分子内部的电子世界提供了新的工具,“使得能够对以前无法遵循的快速过程进行调查”。
诺贝尔物理学委员会主席伊娃・奥尔森说:“我们现在可以打开通往电子世界的大门。阿秒物理学让我们有机会理解由电子控制的机制,下一步将是更好利用它们。”

关于 “阿秒光脉冲”
瑞典皇家科学院表示,三位获奖者的实验产生了 “如此短的光脉冲,以阿秒为单位进行测量”。
首先,让我们想象一个时间尺度:阿秒是 10 的负 18 次方秒,又称阿托秒、渺秒,是一种新发现的 “时间切片”。这是一个非常短暂的时刻,短到仅仅是一秒的百亿亿分之一。长期以来,阿秒作为一个理论上的时间量程而存在。
从比例上来看,一阿秒之于一秒,如同一秒之于 317.1 亿年,约为宇宙年龄的两倍。这是一个非常短暂的时刻,但有巨大的应用潜能。
而 “阿秒光脉冲” 是这样短暂时间内发出的光脉冲。在这样的时间尺度上,科学家们尝试捕捉物质中电子的运动,这就是 “电子动力学” 的研究内容。
电子是原子内部的粒子,它们的移动速度非常快 —— 可达到以十亿分之一秒为单位。此前,它们的运动和行为太快而难以追踪,在最先进的显微镜下看起来仍很模糊。三位得奖科学家所研发的阿秒光脉冲技术就像超高速快门一样,使得我们能直接观察并探索电子在原子和分子中的快速动作。
关于获奖者
皮埃尔・阿戈斯蒂尼教授是美国俄亥俄州立大学名誉教授,目前关于他的资料并不多。

皮埃尔・阿戈斯蒂尼
费伦茨・克劳斯教授是匈牙利裔奥地利人,维也纳工业大学博士,教授,现任德国马克斯普朗克量子光学研究所所长。他是去年沃尔夫物理学奖的获得者。

费伦茨・克劳斯
根据网上资料,1990 年代,他在维也纳技术大学攻读博士学位时,就对用激光产生超短光脉冲感兴趣。2000 年代早期,他的研究小组产生了第一个阿秒脉冲,证明了脉冲时长在阿秒量级,这使克劳斯第一次能够在原子尺度上实时观察电子运动,这项发现也成为他长期以来的研究方向。
安妮・卢利尔是法国 - 瑞典物理学家,现为隆德大学原子物理学教授。她同样是去年沃尔夫物理学奖的获得者,也是第 5 位荣获诺贝尔物理学家的女性科学家(此前 4 位为居里夫人、玛丽亚・格珀特・迈耶、唐娜・斯特里克兰以及安德烈亚・盖兹)。在六个诺贝尔奖中,这是女性获奖者数量第二少的奖项。

安妮・卢利尔
在巴黎大学,她获得数学和理论物理双硕士学位,博士论文研究实验物理。卢利尔研究短而强的激光脉冲与原子之间的相互作用,目前为新阿秒科学研究领域形成的关键参与者。在研究中,她的研究团队使用激光技术产生超短光脉冲,以此窥视微观世界。有了这些 “照相机闪光灯”,就可以研究原子和分子内部的电子运动。
此外,她的研究小组进行的实验为阿秒科学理论描述的发展做出了重大贡献,同时也进行了许多开创性的实验,为原子内部的动力学提供了新的基本科学理解。
(编辑:西西)
汪诘:阿秒激光有何作用?为何它值得荣获诺贝尔奖?
科学声音
发布于 2023-10-04 09:56,IP 属地 上海

2023 年的诺贝尔物理学奖授予了 3 位从事阿秒激光研究的科学家。然而,周围大多数人看到“阿秒激光”这一概念时,犹如看到火星文,对其含义一无所知。希望本文能够为读者提供一些关于阿秒激光的知识。
诺贝尔物理学奖一直以来对激光领域颇为青睐。在 2023 年之前,至少已有 6 个诺贝尔奖与激光的研究和应用相关,而 2023 年又新增了一个与激光相关的奖项。
如果回溯到 1960 年以前,向世界上的任何人描述激光,几乎如同向盲人描述颜色一样,难以让对方理解激光的本质。但在当今时代,仅需 5 元便可购得一支激光笔,甚至幼儿园的小朋友都知晓激光的概念。

不过,对于大多数普通人而言,提及激光,脑海中大概首先想到的一个词便是“颜色”。在我们的认知中,激光呈现出五颜六色的形态。激光颜色的本质实际上是其频率,或者说是波长。波长与频率之间存在着简单的换算关系,它们的乘积等于光速。
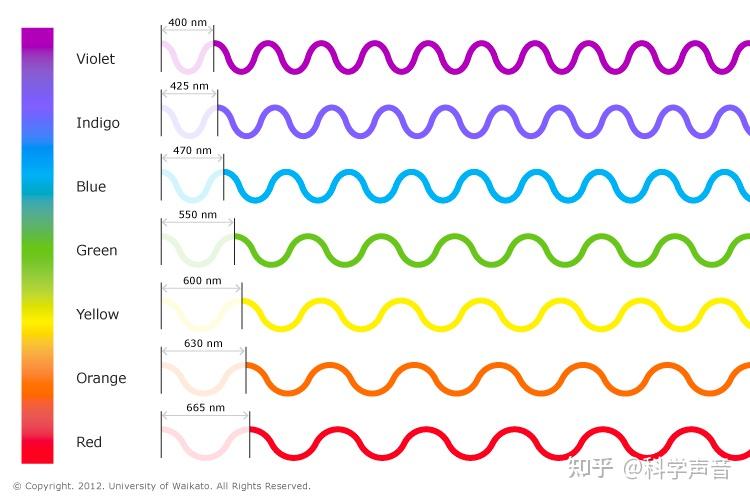
那么,除了颜色之外,还能想到哪些用于描述激光的形容词呢?
是的,或许你会想到亮度。确实如此,激光笔的发射功率越大,其亮度越高,同时也会产生更多的热量。目前市面上销售的一些激光笔,甚至能够点燃火柴。

还有其他的吗?估计很难再想到了吧。
实际上,在专业人士眼中,描述激光还有一个至关重要的参数,即“脉冲宽度”,简称为“脉宽”。
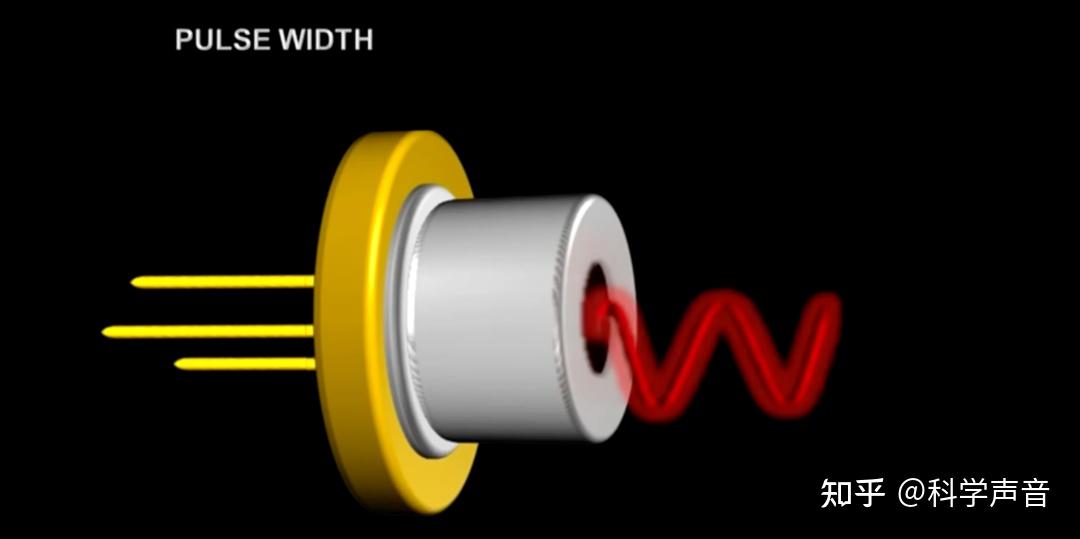
理解阿秒激光的关键在于理解脉宽的概念。
在激光刚被发明时,它是一种连续发出的光。这意味着什么呢?我们可以将激光笔想象成一把滋水枪,发出的激光则如同水流。普通的滋水枪,当扣动扳机时,水流会连续不断地从枪口喷出,这便是连续激光。

然而,也存在一种滋水枪,扣动扳机时,水流会以极短的间隔,一小股一小股地喷出,就如同发射一颗颗水子弹。这种滋水枪通常比连续发射的水枪具有更强的冲击力,能够喷射得更远。

事实上,激光器也是如此。有些激光器能够将激光分割成一小股一小股,并以极短的间隔时间射出,这种激光被称为“脉冲激光”。不过,由于人眼存在视觉残留现象,当脉冲激光的发射频率快到一定程度时,肉眼便无法分辨出一颗颗激光“子弹”,看到的仍然是一束连续的激光。相较于连续激光,脉冲激光的优势在于能够获得更高的功率。将激光脉冲分割得越小,发射频率越快,每一颗激光“子弹”所蕴含的能量也就越大。

科学家将每一个激光脉冲的间隔时间定义为“脉冲宽度”(简称脉宽),因此,脉宽的单位是时间单位。对于一束每隔 1 秒发出一颗“激光子弹”的激光,其脉宽即为 1 秒,我们可以将这种激光称为“秒光”。但对于脉冲激光而言,1 秒的脉宽实在过长,我们需要更短的时间单位来描述它。
于是,便有了“纳秒光”,它表示激光的脉宽为 1 纳秒,即 10 亿分之一秒,用科学计数法表示为 1 0 − 9 10^{-9} 10−9 秒。
脉宽再小一级是“皮秒光”,1 皮秒等于 1 万亿分之一秒,即 1 0 − 12 10^{-12} 10−12 秒。
再小一级是“飞秒光”,1 飞秒等于 1000 万亿分之一秒,即 1 0 − 15 10^{-15} 10−15 秒。
而此次诺贝尔物理学奖所涉及的“阿秒光”,1 阿秒等于 100 亿亿分之一秒,即 1 0 − 18 10^{-18} 10−18 秒。这个数值极其微小,普通人很难形成直观的概念。可以这样说,假如将 1 阿秒想象成 1 秒的时长,那么 1 秒就相当于 317 亿年,比宇宙的年龄还要大一倍多。
因此,阿秒激光是迄今为止人类能够制造出的具有最短时间间隔的物质,制造阿秒激光的方法正是由这几位诺贝尔奖得主所发明的。简单来说,就是使用一束飞秒激光轰击某种惰性气体,从而激发出脉宽更小的阿秒激光。轰击不同的惰性气体,能够产生不同类型的阿秒光。
那么,阿秒激光究竟有何用途?为何它能够荣获诺贝尔奖呢?
阿秒激光的用途极为广泛。总体而言,阿秒激光为人类打开了一扇通往研究电子极端超快运动过程的大门,为进一步探索微观世界提供了强有力的工具。
由于涉及量子物理学领域的知识,想要直接解释清楚几乎是不可能的。作为科普内容,只能通过类比的方式让普通人对其有一个大致的理解。但需要再三强调的是,类比并非真正的物理学,这种理解方式仅可作为一种社交谈资,在饭桌上交流尚可,切不可在此基础上进行无端的想象并自创理论。
对于玩过摄影的人来说,应该能够理解快门速度的概念。
我们要拍摄的对象运动速度越快,就需要越高的快门速度。如果快门速度不够,拍摄出来的照片或视频就会出现拖影现象。

在视频拍摄中,有一个参数叫做“帧率(fps)”,即一秒钟拍摄照片的数量。我们用手机拍摄的视频,帧率一般为 30fps,也就是每秒拍摄 30 张照片,这对于记录日常生活中的画面基本能够满足需求。

然而,如果用手机拍摄水滴入水的画面,基本上无法捕捉到清晰的细节,因为水滴入水的速度太快了。但如果使用高速摄影机来拍摄水滴入水的过程,就能够清晰地呈现出整个过程。

摄影机的帧率越高,就能够记录下更多高速运动对象的细节。


早期的高速摄影机为了获得更高的帧率,采用的方法是拼命提高快门的开合速度,相机中确实存在一个高速开合的“门”。但不难想象,通过这种机械方式来提高快门速度,很快就会达到极限,无法实现更高的速度。

那么,该如何解决这个问题呢?工程师们想到了脉冲激光。仔细思考,脉冲激光的本质与快门颇为相似,都是在一定的间隔时间内完成一次动作。假如有一个物体在做高速运动,我们用一束脉冲激光照射它,理论上它会呈现一亮一暗的状态,就如同摄像机的感光器件被一次次曝光。然后,将物体反射回来的激光收集起来,形成数据流,再通过计算机中的算法还原出被拍摄物体的影像。
可以想象有一把连续发射的机关枪,在枪口前方有一辆快速行驶的汽车。如果子弹的发射频率不够快,很可能无法击中汽车,或者只能击中寥寥几次。反弹回来的子弹越少,我们获取的关于汽车的信息也就越少。
所以,脉宽越小的激光,相当于发射频率越快的激光枪,能够拍摄到运动速度更快的对象。
使用纳秒光可以拍摄到各种化学反应,例如结晶的过程。
使用皮秒光可以拍摄到分子尺度的运动。
使用飞秒光可以拍摄到原子尺度的运动。
而使用阿秒光则可以拍摄到原子内部,即电子尺度的运动。打个比方,阿秒光就如同人类终于制造出了一支能够深入原子内部的探针,直接触及电子。
这便是目前人类能够直接探测到的微观世界的极限。
然而,这是否足够呢?答案是否定的。
未来,我们还需要脉宽更短的激光。1 阿秒,即 100 亿亿分之一秒,听起来已经是一个短到难以想象的时间。但人类已知的最短时间单位是普朗克时间,即 1 0 − 43 10^{-43} 10−43 秒。假如将 1 普朗克时间想象成 1 秒,那么 1 阿秒就相当于 3170 亿亿年,是宇宙年龄的 2300 万倍。
如此看来,人类的寿命似乎也不算短暂,不是吗?
这就是 2023 年的诺贝尔物理学奖所涉及的阿秒激光相关内容。
via:
-
What is time? | Space
https://www.space.com/time-how-it-works -
单个仄秒激光脉冲的产生_百度百科
https://baike.baidu.com/item/单个仄秒激光脉冲的产生/58349338 -
普朗克时间_百度百科
https://baike.baidu.com/item/普朗克时间/2429708 -
数量级 (时间) - 维基百科,自由的百科全书
https://zh.wikipedia.org/wiki/数量级_(时间) -
时间统一系统_百度百科
https://baike.baidu.com/item/时间统一系统/3533847 -
时间统一系统授时方式简介 - 知乎
https://zhuanlan.zhihu.com/p/62301992 -
1 秒的百亿亿分之一:诺贝尔物理学奖授予三位阿秒激光科学家_研究_脉冲_实验
https://www.sohu.com/a/725493716_656058 -
汪诘:阿秒激光有啥用?为啥它值得一个诺贝尔奖? - 知乎 发布于 2023-10-04 09:56,IP 属地 上海
https://zhuanlan.zhihu.com/p/659482197 -
247仄秒!短时测量世界纪录诞生----中国科学院
https://www.cas.cn/kj/202010/t20201020_4763536.shtml -
Meet the zeptosecond, the shortest unit of time ever measured | Live Science
https://www.livescience.com/zeptosecond-shortest-time-unit-measured.html
……





















 4554
4554

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








