注:本文为 “线性代数 | 知识点整理” 相关文章合辑。
因 csdn 篇幅合并超限分篇连载,本篇为 Ref 1。
略作重排,未整理去重。
图片清晰度限于引文原状。
如有内容异常,请看原文。
线性代数知识汇总
Arrow 于 2016-11-27 16:27:57 发布
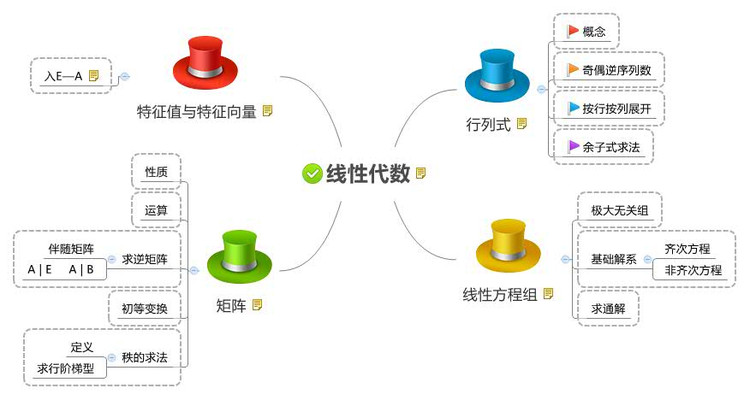
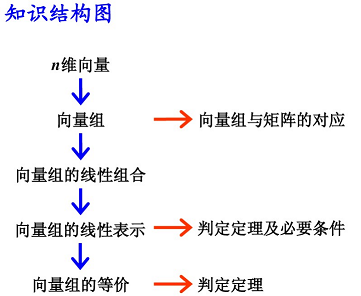
1. 线性代数知识图谱
线性代数是 代数学 的一个分支,主要处理线性关系问题。线性关系即数学对象之间的关系是以一次形式来表达的。例如,在解析几何里,平面上直线的方程是二元一次方程;空间平面的方程是三元一次方程,而空间直线视为两个平面相交,由两个三元一次方程所组成的方程组来表示。含有 n n n 个未知量的一次方程称为线性方程。变量的一次函数称为线性函数。线性关系问题简称线性问题。解线性方程组的问题是最简单的线性问题。
线性(linear)指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数。
非线性(non-linear)则指不按比例、不成直线的关系,一阶导数 不为常数。
行列式非零 ⇔ \Leftrightarrow ⇔ 矩阵可逆 ⇔ \Leftrightarrow ⇔ 方阵满秩 ⇔ \Leftrightarrow ⇔ 向量组满秩(向量个数等于维数)。
2. 行列式
2.1 定义
矩阵的行列式,determinate(简称 det),是基于矩阵所包含的行列数据计算得到的一个标量。是为求解线性方程组而引入的。
2.2 二阶行列式
计算方式:对角线法则
2.3 三阶行列式
计算方式:对角线法则
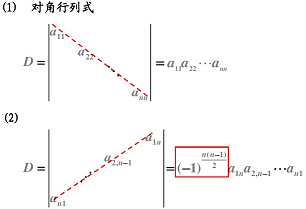
2.4 n 阶行列式
2.4.1 计算排列的逆序数
2.4.2 计算 n 阶行列式
2.4.3 简化计算总结
2.4.4 行列式的 3 种表示方法
2.5 行列式的性质
性质 1:行列式与它的转置行列式相等。
注:行列式中行与列具有同等的地位,行列式的性质凡是对行成立的对列也同样成立。
性质 2:互换行列式的两行(列),行列式变号。
推论:如果行列式有两行(列)完全相同,则此行列式为零。
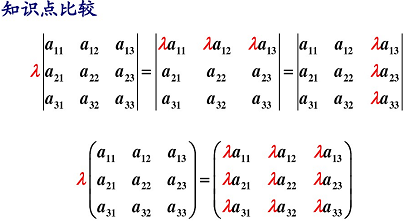
性质 3:行列式的某一行(列)中所有的元素都乘以同一个倍数 k,等于用数 k 乘以此行列式。
推论:行列式的某一行(列)中所有元素的公因子可以提到行列式符号的外面。
性质 4:行列式中如果有两行(列)元素成比例,则此行列式为零。
性质 5:若行列式的某一列(行)的元素都是两数之和,则等于对应的两个行列式之和。
性质 6:把行列式的某一列(行)的各元素乘以同一个倍数然后加到另一列(行)对应的元素上去,行列式不变。
2.6 计算行列式的方法
-
利用定义
-
利用性质把行列式化为上三角形行列式,从而算得行列式的值
定理中包含着三个结论:
-
方程组有解(解的存在性)。
-
解是唯一的(解的唯一性)。
-
解可以由公式 (2 =700x) 给出。
定理 4:如果线性方程组 (1 =700x) 的系数行列式不等于零,则该线性方程组一定有解,而且解是唯一的。
定理 4′:如果线性方程组无解或有两个不同的解,则它的系数行列式必为零。
齐次线性方程组的相关定理
定理 5:如果齐次线性方程组的系数行列式 D 不等于 0,则齐次线性方程组只有零解,没有非零解。
定理 5′:如果齐次线性方程组有非零解,则它的系数行列式必为零。
- 用克拉默法则解线性方程组的两个条件
1 =700x) 方程个数等于未知量个数。
2 =700x) 系数行列式不等于零。
- 克拉默法则的意义主要在于建立了线性方程组的解和已知的系数以及常数项之间的关系。它主要适用于理论推导。
2.8 行列式按行(列)展开
对角线法则只适用于二阶与三阶行列式。
本节主要考虑如何用低阶行列式来表示高阶行列式。
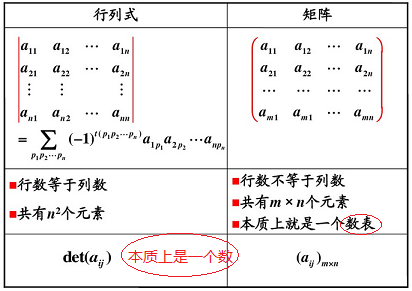
3. 矩阵
3.1 矩阵的定义
3.1.1 矩阵与行列式的区别
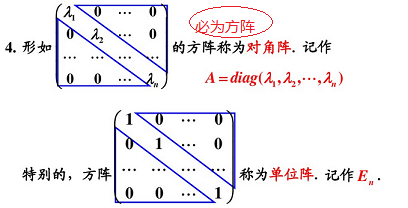
3.2 特殊矩阵
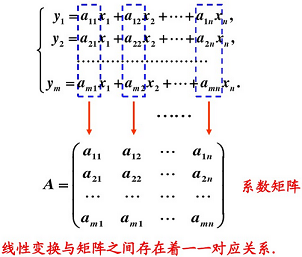
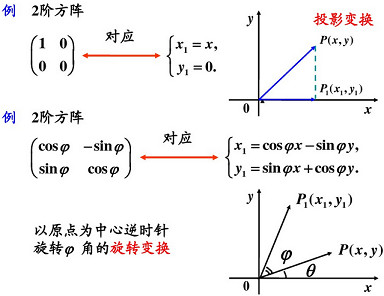
3.3 矩阵与线性变换
3.4 矩阵的运算
3.4.1 矩阵的加法
行列式与矩阵加法的比较:
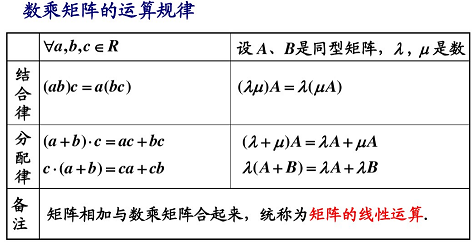
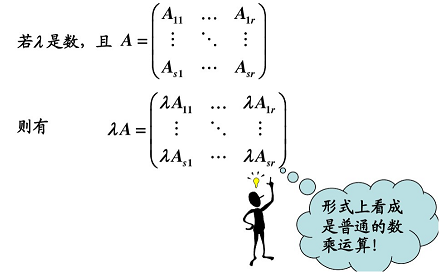
3.4.2 数乘矩阵
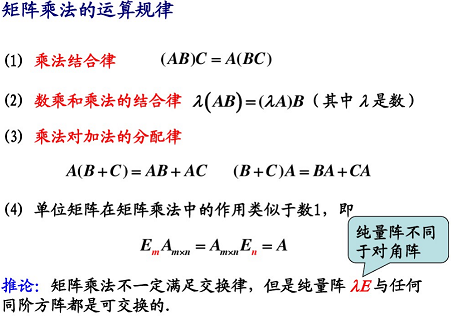
3.4.3 矩阵与矩阵相乘
3.4.4 矩阵的转置
反对称矩阵(skew symmetric matrix)
3.4.5 方阵的行列式
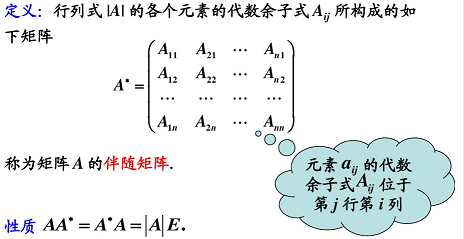
3.4.6 伴随矩阵
3.4.7 共轭矩阵
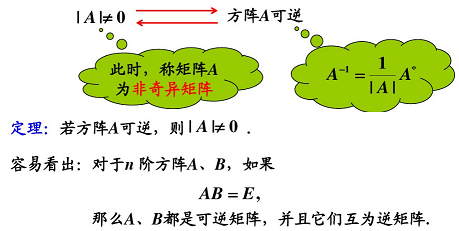
3.5 可逆矩阵(或称非奇异矩阵)
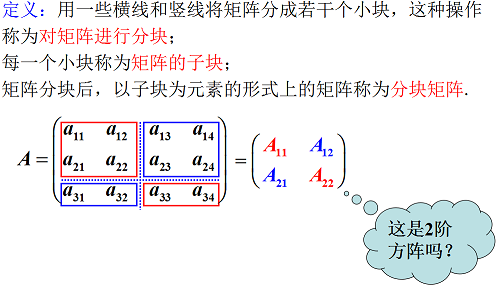
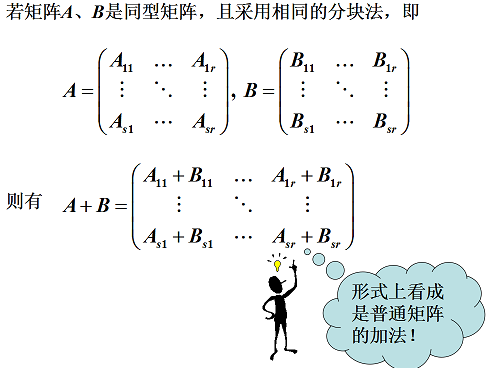
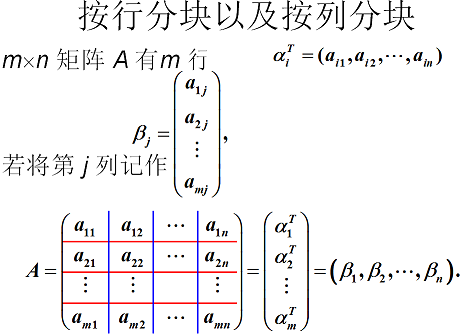
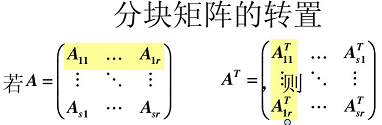
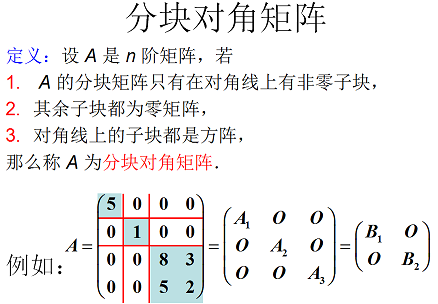
3.6 矩阵分块法
分块矩阵不仅形式上进行转置,而且每一个子块也进行转置。
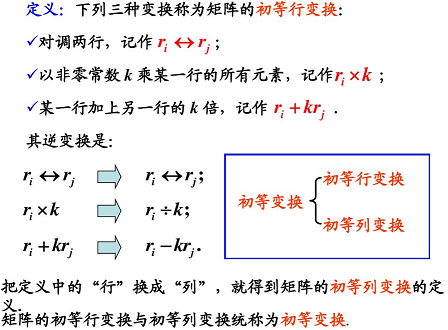
4. 矩阵的初等变换与线性方程组
4.1 矩阵的初等变换
4.2 矩阵之间的等价关系
4.3 初等变换与矩阵乘法的关系
4.4 矩阵的秩
4.5 线性方程组的多解
4. 向量组的线性相关性
4.1 向量组及其线性组合
4.2 向量组的线性相关性
4.3 向量组的秩
结论:矩阵的最高阶非零子式一般不是唯一的,但矩阵的秩是唯一的。
4.4 线性方程组的解的结构
问题:什么是线性方程组的解的结构?
答:所谓线性方程组的解的结构,就是当线性方程组有无限多个解时,解与解之间的相互关系。
备注:
-
当方程组存在唯一解时,无须讨论解的结构。
-
下面的讨论都是假设线性方程组有解。
4.5 向量空间
4.5.1 封闭的概念
定义:所谓封闭,是指集合中任意两个元素作某一运算得到的结果仍属于该集合。
4.5.2 向量空间的概念
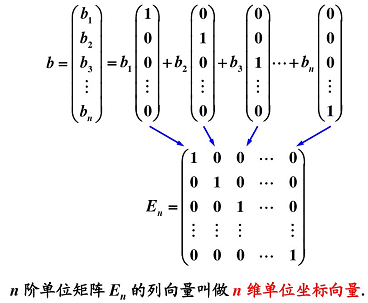
定义:设 V V V 是 n n n 维向量的集合,如果
① 集合 V V V 非空,
② 集合 V V V 对于向量的加法和乘数两种运算封闭,
具体地说,就是:
若 a ∈ V a \in V a∈V, b ∈ V b \in V b∈V,则 a + b ∈ V a + b \in V a+b∈V。(对加法封闭)
若 a ∈ V a \in V a∈V, l ∈ R l \in R l∈R,则 l a ∈ V l a \in V la∈V。(对乘数封闭)
那么就称集合 V V V 为向量空间。
4.5.3 子空间的概念
定义:如果向量空间 V V V 的非空子集合 V 1 V1 V1 对于 V V V 中所定义的加法及乘数两种运算是封闭的,则称 V 1 V1 V1 是 V V V 的子空间。
4.5.4 向量空间的基的概念
5. 相似矩阵及二次型
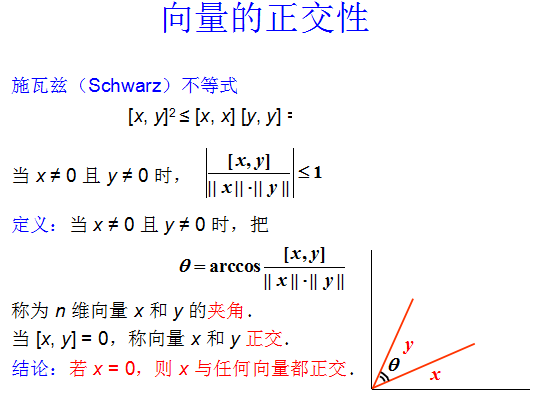
5.1 向量的内积、长度及正交性
5.1.1 向量的内积
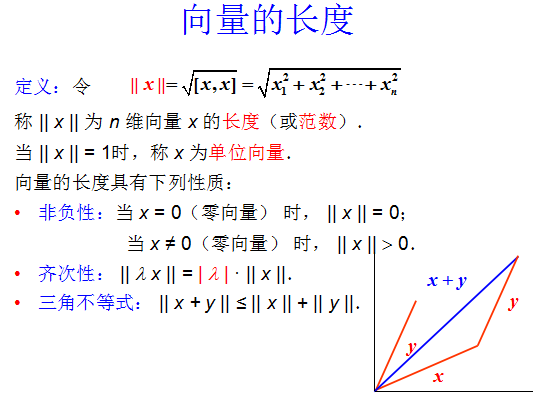
5.1.2 向量的长度或范数
单位向量:长度为 1 的向量。
5.1.3 向量的正交性
向量正交:向量内积为 0。
5.1.4 正交矩阵或正交阵
5.1.5 正交矩阵的性质
5.2 方阵的特征值与特征向量
5.2.1 正定矩阵 / 半正定矩阵
5.3 相似矩阵
5.4 对称矩阵的对角化
5.5 二次型及其它标准型
线性代数知识点整理
圆气鹿酱 于 2020-10-04 23:51:23 发布
矩阵等价与矩阵相似
等价:A 经过一系列初等变换等到 B,称 A 与 B 等价,也就是存在可逆阵 P、Q 使 B = P A Q B=PAQ B=PAQ,那么 A、B 秩相等。
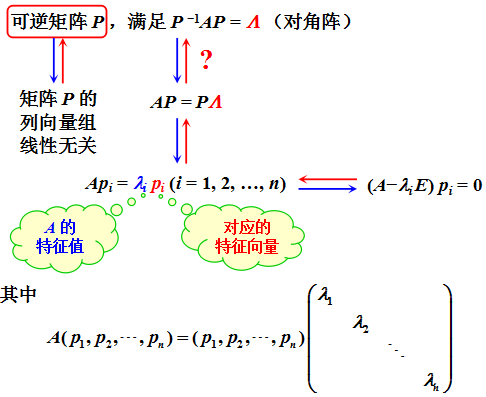
相似:在线性代数中,相似矩阵是指存在相似关系的矩阵。设 A,B 为 n 阶矩阵,如果有 n 阶可逆矩阵 P 存在,使得 P − 1 A P = B P^{-1} AP=B P−1AP=B,则称矩阵 A 与 B 相似,记为 A ∼ B A \sim B A∼B。
相似矩阵的特点:
- 两者的秩相等。
- 两者的行列式值相等。
- 两者拥有同样的特征值,尽管相应的特征向量一般不同。
- 两者拥有同样的特征多项式。
行列式计算技巧
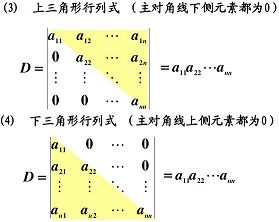
- 上三角行列式的值为主对角线数字乘积。
矩阵的初等变换与行列式值的关系
第一类初等变换(换行换列)使行列式变号,第二类初等变换(某行或某列乘 k 倍)使行列式变 k 倍,第三类初等变换(某行(列)乘 k 倍加到另一行(列))使行列式不变。
矩阵的特征值(特征根)和特征向量
-
A 必须是方阵。
-
A α = λ α A\alpha = \lambda\alpha Aα=λα( λ \lambda λ 可以为 0,特征向量 α \alpha α 是非 0 列向量)。
-
一个特征值可以对应多个特征向量,一个特征向量只能对应一个特征值。
-
特征多项式: ∣ A − λ E ∣ |A - \lambda E| ∣A−λE∣。
-
特征方程: ∣ A − λ E ∣ = 0 |A - \lambda E| = 0 ∣A−λE∣=0。
-
λ \lambda λ 是 A 的特征值, α \alpha α 是对应的特征向量,则 c α c\alpha cα 也是对应的特征向量( c ≠ 0 c \ne 0 c=0)。
-
α 1 , α 2 \alpha_1, \alpha_2 α1,α2 是 λ \lambda λ 的特征向量,则 c 1 α 1 + c 2 α 2 c_1\alpha_1 + c_2\alpha_2 c1α1+c2α2 也是特征向量(前提是同一个特征值)。
-
在解特征方程的时候若出现 ( λ − 2 ) ( λ − 1 ) ( λ − 1 ) = 0 (\lambda - 2)(\lambda - 1)(\lambda - 1) = 0 (λ−2)(λ−1)(λ−1)=0,结论写成 A 的特征值为 λ 1 = 2 , λ 2 = λ 3 = 2 \lambda_1 = 2, \lambda_2 = \lambda_3 = 2 λ1=2,λ2=λ3=2(重根要写出来)。
-
不同特征根的特征向量是线性无关的。
-
若 n 阶方阵 A 可以相似于一个 n 阶对角矩阵,则称 A 可对角化,n 阶方阵 A 相似于对角矩阵的充要条件是 A 有 n 个线性无关的特征向量。
-
特征值为 0,则行列式的值为 0。
-
特征值正是使得 ∣ λ E − A ∣ = 0 | \lambda E - A| = 0 ∣λE−A∣=0 的那些根(可以用来一眼看出特征值)。
-
特征向量的求法: ( A − λ E ) α = 0 (A - \lambda E)\alpha = 0 (A−λE)α=0。
-
特征值的积为行列式的值。
-
特征值的和为矩阵的迹。
-
特征值和特征向量的性质:
-
转置后特征值不变。
-
设 λ \lambda λ 是 A 的特征值, λ k \lambda^k λk 是 A k A^k Ak 的特征值。
-
f ( λ ) = a 0 + a 1 λ + ⋯ + a m λ m f(\lambda) = a_0 + a_1\lambda + \cdots + a_m\lambda^m f(λ)=a0+a1λ+⋯+amλm 是 f ( A ) = a 0 E + a 1 A + ⋯ + a m A m f(A) = a_0E + a_1A + \cdots + a_mA^m f(A)=a0E+a1A+⋯+amAm 的特征值。
-
λ \lambda λ 是可逆方阵 A 的特征值, 1 λ \frac{1}{\lambda} λ1 是 A − 1 A^{-1} A−1 的特征值。
-
逆矩阵与伴随矩阵与原来的矩阵有相同的特征向量。
-
矩阵和的特征值等于特征值的和。
方阵的行列式
-
∣ k A ∣ = k n ∣ A ∣ |kA| = k^n|A| ∣kA∣=kn∣A∣(因为 k A kA kA 是用 k k k 乘 A A A 里面的所有数)。
-
∣ A B C ∣ = ∣ A ∣ ∣ B ∣ ∣ C ∣ |ABC| = |A||B||C| ∣ABC∣=∣A∣∣B∣∣C∣(A、B、C 同阶方阵)。
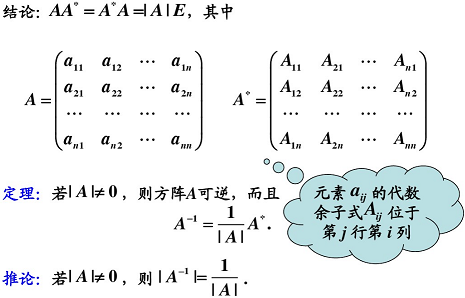
伴随矩阵与逆矩阵
-
求伴随矩阵(任意方阵都有伴随矩阵):
-
求出所有元素的代数余子式。
-
按行求的代数余子式按列放构成矩阵 A ∗ A^* A∗。
-
-
一个方阵与其伴随矩阵的秩的关系:
-
若 R ( A ) = n R(A) = n R(A)=n, R ( A ∗ ) = n R(A^*) = n R(A∗)=n。
-
若 R ( A ) = n − 1 R(A) = n - 1 R(A)=n−1, R ( A ∗ ) = 1 R(A^*) = 1 R(A∗)=1。
-
若 R ( A ) < n − 1 R(A) < n - 1 R(A)<n−1, R ( A ∗ ) = 0 R(A^*) = 0 R(A∗)=0(即伴随矩阵为零矩阵)。
-
-
逆矩阵:
-
对角矩阵的逆矩阵为各元素的倒数。
-
A B = A C AB = AC AB=AC, B = C B = C B=C 的条件是 A A A 为可逆矩阵,因为左乘 A A A 的逆即可。
-
逆矩阵的行列式为原矩阵的倒数。
-
逆矩阵的特征值也为原矩阵的倒数。
-
-
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = |A|E AA∗=A∗A=∣A∣E。
- 当 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0, ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*| = |A|^{n - 1} ∣A∗∣=∣A∣n−1。
-
( A ∗ ) − 1 = A ∣ A ∣ (A^*)^{-1} = \frac{A}{|A|} (A∗)−1=∣A∣A。
- ( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1} = \frac{1}{\lambda} A^{-1} (λA)−1=λ1A−1。
向量间的线性关系
-
零向量可被任一向量组表示, k k k 全取 0。
-
含零向量的任意向量组必线性相关。
-
一个零向量必相关,一个非零向量必无关。
-
一个向量组中,部分线性相关则整体线性相关。整体组线性无关,则部分线性无关。
-
线性无关的向量组,其接长向量组也无关。
-
线性相关的向量组,其截短向量组也相关。
-
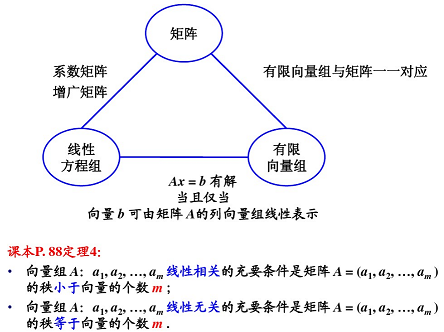
n n n 个 n n n 维向量, D ≠ 0 D \ne 0 D=0,则线性无关。
-
D = 0 D = 0 D=0,线性相关。(都是充要条件)
-
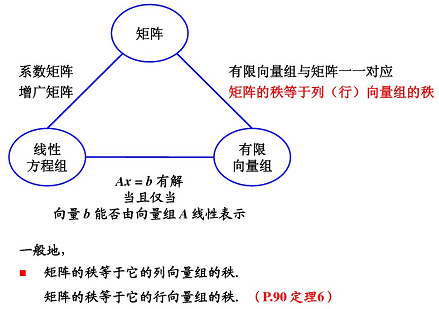
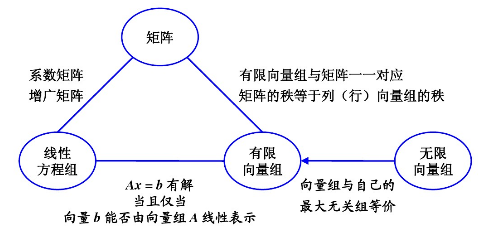
若向量组 A A A: a 1 , a 2 , … , a m a_1, a_2, \ldots, a_m a1,a2,…,am 线性无关,向量组 B B B: a 1 , a 2 , a 3 , … , a m , b a_1, a_2, a_3, \ldots, a_m, b a1,a2,a3,…,am,b 线性相关,则向量 b b b 必能由向量组 A A A 线性表示,且表示法唯一。
-
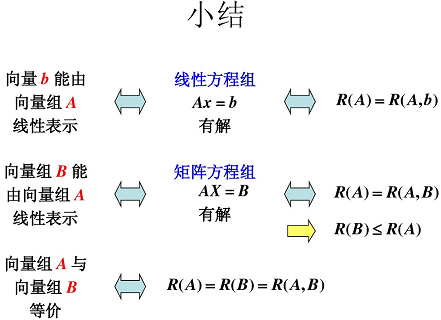
向量 B B B 能由向量组 A A A 线性表示,则 A A A 的秩大于等于 B B B 的秩。
向量组的秩(非 0 子式的最高阶数)
-
极大线性无关组 A 0 A_0 A0 定义:
-
向量组 A 0 A_0 A0: a 1 , a 2 , … , a r a_1, a_2, \ldots, a_r a1,a2,…,ar 线性无关。
-
A A A 中的任何向量均可由向量组 A 0 A_0 A0: a 1 , a 2 , a 3 , … , a r a_1, a_2, a_3, \ldots, a_r a1,a2,a3,…,ar 线性表示。
-
-
极大线性无关组:
-
一个线性无关的向量组其极大线性无关组是本身。
-
任何一个向量组和它的极大线性无关组等价。
-
极大线性无关组中所含向量个数为矩阵的秩。
-
-
零向量的秩为 0。
-
KaTeX parse error: Can't use function '\)' in math mode at position 16: r(A) \leq \min(\̲)̲向量的个数,向量的维数)$。
-
r ( A B ) ≤ min ( r ( A ) , r ( B ) ) r(AB) \leq \min(r(A), r(B)) r(AB)≤min(r(A),r(B))。
-
max ( R ( A ) , R ( B ) ) ≤ R ( A , B ) ≤ R ( A ) + R ( B ) \max(R(A), R(B)) \leq R(A, B) \leq R(A) + R(B) max(R(A),R(B))≤R(A,B)≤R(A)+R(B)。
-
R ( A + B ) ≤ R ( A ) + R ( B ) R(A + B) \leq R(A) + R(B) R(A+B)≤R(A)+R(B)。
-
初等行变换不改变列向量的线性关系。
-
一个向量乘可逆矩阵,秩不变。
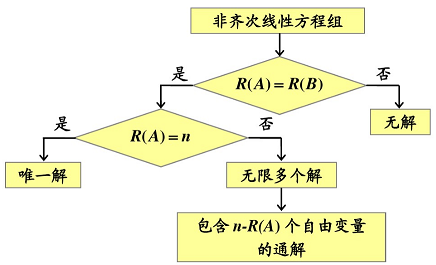
非齐次和齐次线性方程组有解判定
-
线性方程组的向量表示形式
x 1 α 1 + x 2 α 2 + x 3 α 3 + ⋯ = β x_1\alpha_1 + x_2\alpha_2 + x_3\alpha_3 + \cdots = \beta x1α1+x2α2+x3α3+⋯=β
-
线性方程组有解判定( n n n 是未知量的个数)(不齐次的情况,即 A x = b Ax = b Ax=b( b ≠ 0 b \ne 0 b=0))
r ( a ˉ ) = r ( a ) r(\bar{a}) = r(a) r(aˉ)=r(a) 时,方程组有解,等于 n n n 有一个解;小于 n n n 有无穷多解; r ( a ˉ ) ≠ r ( a ) r(\bar{a}) \ne r(a) r(aˉ)=r(a),无解。
-
A x = 0 Ax = 0 Ax=0 有解判定( m m m 为方程个数)
r ( A ) ≤ min ( n , m ) r(A) \leq \min(n, m) r(A)≤min(n,m)。
当 m < n m < n m<n 时,一定有无穷多解,即有非零解。
-
基础解系一定是线性无关的,并且是解向量的极大线性无关组,即每一个解向量都可以由基础解系表示。
正交向量
-
x x x, y y y 内积为 0 时称为正交(或垂直)。
-
若一个向量组中任意两个向量都正交,则称此向量组为正交向量组,若一个向量组中每一个向量都是单位向量,则称此向量组为正交规范向量组或标准正交向量组。
-
实矩阵是指矩阵中每个数都是实数的矩阵。
-
A A T = E A A^T = E AAT=E 或 A T A = E A^T A = E ATA=E,则 n n n 阶实矩阵 A A A 称为正交矩阵。 A A A 为正交矩阵的充要条件是 A A A 的行(列)向量组为正交规范向量组。
-
正交矩阵的性质:
-
∣ A ∣ ∣ A T ∣ = 1 |A| |A^T| = 1 ∣A∣∣AT∣=1,所以 ∣ A ∣ = 1 |A| = 1 ∣A∣=1 或 -1。
-
若 n n n 阶方阵满足 A A T = E AA^T = E AAT=E(即 A − 1 = A T A^{-1} = A^T A−1=AT),称 A A A 为正交矩阵。
-
其次线性方程组解的结构
-
基础解系解的个数是 n − r n - r n−r 个。
-
A x = 0 Ax = 0 Ax=0
A = ( α 1 , α 2 , α 3 ) A = (\alpha_1, \alpha_2, \alpha_3) A=(α1,α2,α3)
x = ( 1 , 2 , 3 ) T x = (1, 2, 3)^T x=(1,2,3)T 的实质是 α 1 + 2 α 2 + 3 α 3 = 0 \alpha_1 + 2\alpha_2 + 3\alpha_3 = 0 α1+2α2+3α3=0。
非齐次线性方程组解的结构
-
若 α 1 , α 2 \alpha_1, \alpha_2 α1,α2 均为 A x = b Ax = b Ax=b 的解,则 α 1 − α 2 \alpha_1 - \alpha_2 α1−α2 为 A x = 0 Ax = 0 Ax=0 的解。
-
α 0 \alpha_0 α0 是 A x = b Ax = b Ax=b 的解, η \eta η 是 A x = 0 Ax = 0 Ax=0 的解,则 α 0 + η \alpha_0 + \eta α0+η 是 A x = b Ax = b Ax=b 的解。
-
A X = b AX = b AX=b 的通解是 A X = b AX = b AX=b 的特解加上 A X = 0 AX = 0 AX=0 的基础解系的线性组合。
分块矩阵
-
分块矩阵的转置:
-
将块看作元素求矩阵的转置。
-
每个子块求转置。
-
-
分块矩阵求行列式
H = ( A C 0 B ) H = \begin{pmatrix} A & C \\ 0 & B \\ \end{pmatrix} H=(A0CB)
∣ H ∣ = ∣ A ∣ ∣ B ∣ |H| = |A||B| ∣H∣=∣A∣∣B∣
H = ( 0 A B C ) H = \begin{pmatrix} 0 & A \\ B & C \\ \end{pmatrix} H=(0BAC)
∣ H ∣ = ( − 1 ) m n ∣ A ∣ ∣ B ∣ |H| = (-1)^{mn}|A||B| ∣H∣=(−1)mn∣A∣∣B∣(可由 Laplace 定理证明)
-
分块矩阵求逆矩阵
( A 0 0 B ) − 1 = ( A − 1 0 0 B − 1 ) \begin{pmatrix} A & 0 \\ 0 & B \\ \end{pmatrix}^{-1} = \begin{pmatrix} A^{-1} & 0 \\ 0 & B^{-1} \\ \end{pmatrix} (A00B)−1=(A−100B−1)
( 0 A B 0 ) − 1 = ( 0 B − 1 A − 1 0 ) \begin{pmatrix} 0 & A \\ B & 0 \\ \end{pmatrix}^{-1} = \begin{pmatrix} 0 & B^{-1} \\ A^{-1} & 0 \\ \end{pmatrix} (0BA0)−1=(0A−1B−10)
实对称矩阵的对角化
-
α \alpha α 的长度表示为 ∣ ∣ α ∣ ∣ ||\alpha|| ∣∣α∣∣,
( α , α ) = ∣ ∣ α ∣ ∣ 2 (\alpha, \alpha) = ||\alpha||^2 (α,α)=∣∣α∣∣2
-
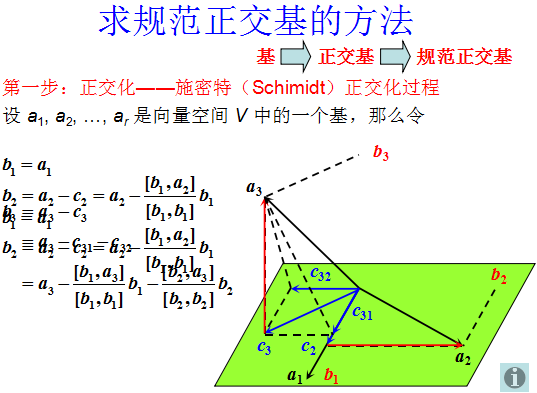
施密特正交化
将一组线性无关的向量组 α 1 , α 2 , … , α r \alpha_1, \alpha_2, \ldots, \alpha_r α1,α2,…,αr 转化为与之等价的正交向量组 β 1 , β 2 , … , β r \beta_1, \beta_2, \ldots, \beta_r β1,β2,…,βr
β 1 = α 1 \beta_1 = \alpha_1 β1=α1
β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1, \beta_1)}\beta_1 β2=α2−(β1,β1)(α2,β1)β1
β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 \beta_3 = \alpha_3 - \frac{(\alpha_3, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_3, \beta_2)}{(\beta_2, \beta_2)}\beta_2 β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
β r = α r − ( α r , β 1 ) ( β 1 , β 1 ) β 1 − ( α r , β 2 ) ( β 2 , β 2 ) β 2 − ⋯ − ( α r , β r − 1 ) ( β r − 1 , β r − 1 ) β r − 1 \beta_r = \alpha_r - \frac{(\alpha_r, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_r, \beta_2)}{(\beta_2, \beta_2)}\beta_2 - \cdots - \frac{(\alpha_r, \beta_{r-1})}{(\beta_{r-1}, \beta_{r-1})}\beta_{r-1} βr=αr−(β1,β1)(αr,β1)β1−(β2,β2)(αr,β2)β2−⋯−(βr−1,βr−1)(αr,βr−1)βr−1
-
实对称矩阵的相似理论
-
设 A A A 为 n n n 阶实对称矩阵,则存在正交矩阵,使得 P T A P = Λ P^TAP = \Lambda PTAP=Λ( Λ \Lambda Λ 是对角矩阵)。
-
n n n 阶方阵相似于对角矩阵的充要条件是由 n n n 个线性无关的特征向量。
-
实对称矩阵 A A A 的属于不同特征值的特征向量相互正交。
-
注意事项:
-
奇异矩阵的秩不是满秩,也叫降秩矩阵, ∣ A ∣ = 0 |A| = 0 ∣A∣=0。非奇异矩阵为满秩矩阵,行列式不为 0, ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0。
-
矩阵乘法一般不满足交换律,满足结合律。
-
初等矩阵定义:单位矩阵经过一次初等变换得到的矩阵(初等矩阵一定可逆)。
-
( A T ) − 1 = ( A − 1 ) T (A^T)^{-1} = (A^{-1})^{T} (AT)−1=(A−1)T
-
矩阵左乘行变换,右乘列变换。
-
反对称矩阵必有 a i j = − a j i a_{ij} = -a_{ji} aij=−aji,所以对角线上的元素都是 0。
-
n n n 阶子式的定义:在 m × n m \times n m×n 矩阵 A A A 中,任取 k k k 行与 k k k 列( k ≤ m k \leq m k≤m, k ≤ n k \leq n k≤n),位于这些行列式交叉处的 k 2 k^2 k2 个元素,不改变它们在 A A A 中所处的位置次序而的 k k k 阶行列式,称为矩阵 A A A 的 k k k 阶子式。
线性代数知识点整理
cuguanren 于 2022-07-06 15:15:46 发布
前言
为了更好地学习深度学习的相关内容,笔者重新整理了线性代数的主要内容,并以知识点摘要的形式对各部分进行了总结,留待之后进行相关概念的快速复习。
一 行列式
1. 行列式求值
参考 行列式求值(链接已沉寂)
2. 七大性质

3. 特殊行列式的值

二 矩阵及其运算
1. 行列向量:
在线性代数中,列向量是一个 n × 1 n \times 1 n×1 的矩阵,即矩阵由一个含有 n n n 个元素的列所组成:列向量的转置是一个行向量,反之亦然。
2. 可逆矩阵:
矩阵 A A A 为 n n n 阶方阵,若存在 n n n 阶矩阵 B B B,使得矩阵 A A A、 B B B 的乘积为单位阵,则称 A A A 为可逆阵, B B B 为 A A A 的逆矩阵。若方阵的逆阵存在,则称为可逆矩阵或非奇异矩阵,且其逆矩阵唯一。 A A A 是可逆矩阵的充分必要条件是 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0(方阵 A A A 的行列式不等于 0)。 A A A 的秩等于 n n n( A A A 满秩)。
3. 常用性质:

4. 伴随矩阵:

三 矩阵的初等变换和线性方程组
1. 初等变换:
单位矩阵通过三种变换形式得到的矩阵叫做初等矩阵
① 行间或列间互换
② 行或列乘 k k k 倍
③ 某行加上另一行的 k k k 倍(列也如此)


2. 矩阵的秩:定义,特性,求秩
细致内容参考 矩阵的秩,重点强调:可逆矩阵是满秩矩阵

3. 齐次与非齐次线性方程组
① 两者区别
齐次线性方程组的常数项全部为零,非齐次方程组的常数项不全为零。
② 表达式不同:
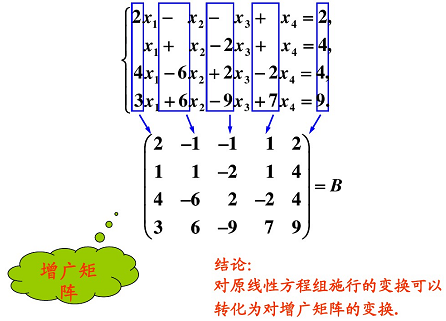
齐次线性方程组表达式: A x = 0 Ax = 0 Ax=0;非齐次方程组常数项不全为零: A x = b Ax = b Ax=b。 A A A 称为系数矩阵,等号右边是常数项。
③ 增广矩阵
又称 广置矩阵 ,是在 线性代数中系数矩阵 A A A 的右边添上线性方程组等号右边的常数列得到的矩阵,用矩阵( A ∣ B A|B A∣B)表示

④ 两种方程组的解

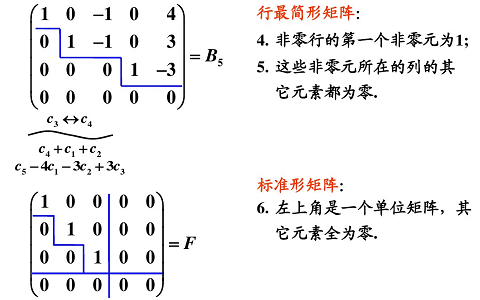
⑤ 最简行 / 列阶梯矩阵:
-
只能行变换。
-
化简时,从左上角第一个非零元素开始,其下元素需全部化为零,再找阶梯下一个元素,其下元素化为零。
-
行阶梯接着可化为行最简,阶梯每行左起第一个元素为 1。
-
行变换只能化为行最简,列一样。
因此,不能交叉使用两种变换得到一种最简矩阵。
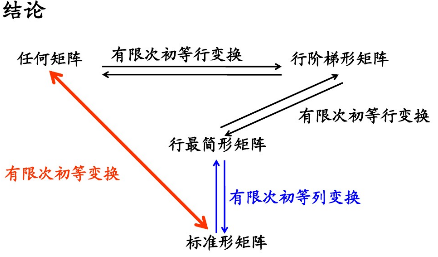
4. 等价矩阵:
在线性代数和矩阵论中,有两个 m × n m \times n m×n 阶矩阵 A A A 和 B B B,如果这两个矩阵满足 B = Q A P B = QAP B=QAP( P P P 是 n × n n \times n n×n 阶可逆矩阵, Q Q Q 是 m × m m \times m m×m 阶可逆矩阵),那么这两个矩阵之间是等价关系。也就是说,存在可逆矩阵( P P P、 Q Q Q),使得 A A A 经过有限次的初等变换得到 B B B。
四 向量组的线性相关性
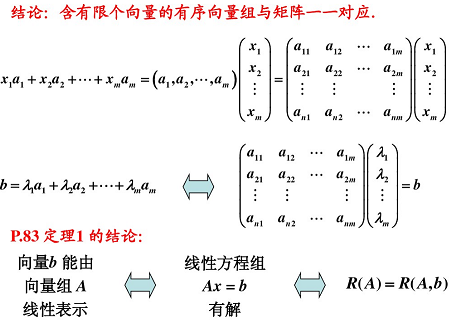
1. 线性表示:
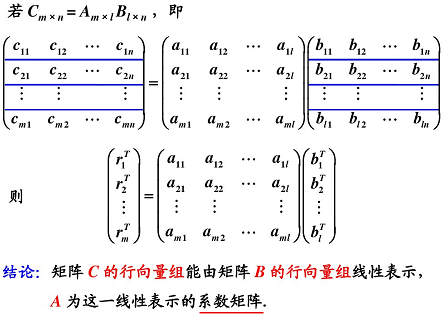
对于两个向量组:两个向量组 A A A、 B B B,若 A A A 组中每一个向量都可以由向量组 B B B 线性表示,则称向量组 A A A 可由向量组 B B B 线性表示。(向量 b b b 能由向量组 X X X 线性表示的充要条件是: R ( A ) = R ( A , B ) R(A) = R(A, B) R(A)=R(A,B))
系数矩阵在左边时可以认为是对行进行线性变换,在右边时可以认为对列进行线性变换。
2. 线性相关性判断:
定义由第一种方法给出, A A A 向量组的构成元素 a i a_i ai 都是向量
初等行变换不改变列向量的线性相关性,也不改变行向量的线性相关性。

3. 解的情况

五 相似矩阵以及二次型
只有方阵具有特征值与特征向量,不同特征值所对应的特征向量之间线性无关
形象的例子:如果把矩阵看作运动的话,那么
-
特征值就是运动的速度
-
特征向量是运动的方向
1. 特征值和特征向量的定义
实数 λ \lambda λ 为特征值,向量 p p p 为特征向量

2. 特征值和特征向量的求解

3. 特征值和特征向量的性质

4. 矩阵的相似对角化
存在可逆矩阵 P P P 使得矩阵 A A A 满足 P − 1 A P = A P^{-1} A P = A P−1AP=A 的对角矩阵(尖符号),则 A A A 称为可以相似对角化

5. 特征分解和对角矩阵

6. 二次化标准型
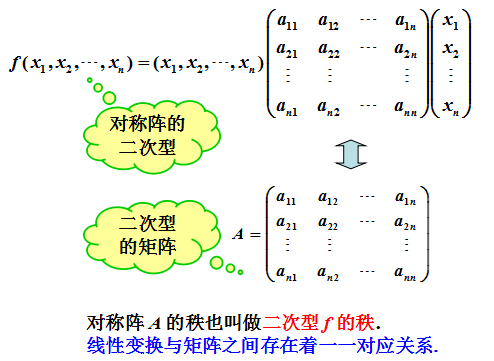
考虑到对于深度学习来说,此部分不太重要,暂时进行了略过,留待后日补充。

线性代数知识点总结,基础概念和计算整理(手写版)
李问号 已于 2022-11-08 22:18:59 修改
线性代数中一定必须要掌握的基础概念和计算的整理,简单易懂,适合入门和复习。









Ref 2 / 3
-
线性代数 | 知识点整理 Ref 2-CSDN博客
https://blog.csdn.net/u013669912/article/details/147263760 -
线性代数 | 知识点整理 Ref 3-CSDN博客
https://blog.csdn.net/u013669912/article/details/147253667
via:
-
线性代数精要-CSDN博客
https://blog.csdn.net/myarrow/article/details/53365048 -
线性代数知识点整理(自用)-CSDN博客
https://blog.csdn.net/m0_46882548/article/details/108198329 -
线性代数知识点整理_总结-CSDN博客
https://blog.csdn.net/cuguanren/article/details/125640237 -
线性代数知识点总结,基础概念和计算整理(手写版)-CSDN博客
https://blog.csdn.net/Bluebro/article/details/127630205












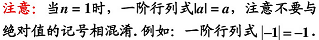
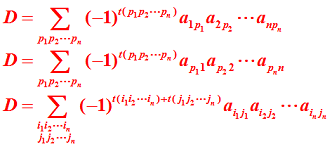
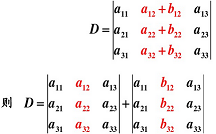
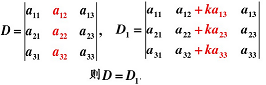












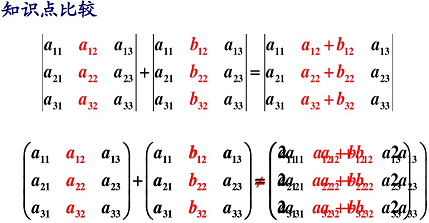




















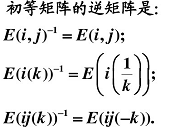






















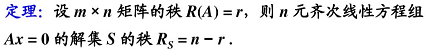













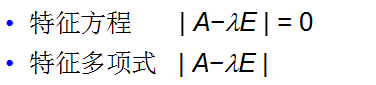









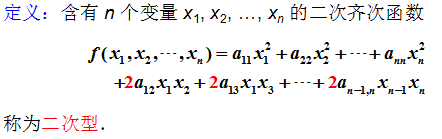























 3363
3363

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








