格密码学习笔记（五）：对偶格

最新推荐文章于 2024-01-06 00:37:48 发布

博客已停更

最新推荐文章于 2024-01-06 00:37:48 发布

阅读量593

点赞数

分类专栏：现代密码学基础文章标签：格密码现代密码学后量子密码

本文链接：https://blog.csdn.net/u014134327/article/details/129528203

版权

现代密码学基础专栏收录该内容

22 篇文章 50 订阅

订阅专栏

文章目录

对偶空间
对偶格
格分层
Banaszczyk定理
BDD问题规约至SIVP问题上
已知格基，如何求对偶格基
致谢

对偶空间

$\mathbb{R}$ 上的向量空间 $V$ 满足以下2个性质：

向量加法操作 $\bm{x} + \bm{y} \in V$ ；
标量乘法操作 $\cdot \bm{x} \in V$ 。

线性空间里面有一个很重要的概念叫对偶空间（Dual Space）。具体可以参考
怎么形象地理解对偶空间（Dual Vector Space）？ - 石在的回答 - 知乎

在 $V$ 上的线性泛函 $\phi$ 是一个从 $V$ 到 $\mathbb{R}$ 的线性映射，即 $\phi: V \to \mathbb{R}$ 。一般而言，对于 $\bm{x} \in V$ ，有 $\phi_{\bm{y}}(\bm{x}) = \langle \bm{x}, \bm{y} \rangle$ 。

定义： $V$ 的对偶空间 $V^\vee$ 是所有 $\phi$ 构成的向量空间。

举一个例子：假想 $\bm{x} \in V$ 是表示橘子的一个特征向量，每个维度/属性可以是维生素、糖分等，不同 $\bm{x}$ 表征不同橘子；线性泛函 $\bm{y}$ 每个维度规定维生素的价值、糖分的价值等， $\langle \bm{x}, \bm{y} \rangle$ 算出一个橘子的具体价格；若 $\bm{y}$ 固定而 $\bm{x}$ 变化，可以推算出特定规格标准下不同规格的橘子的价格；若 $\bm{x}$ 固定而 $\bm{y}$ 变化，可以推算出同一个橘子在不同规格标准下的价格。

对偶格

定义（对偶格，Dual Lattice） 记 $\Lambda$ 为一个格， $\mathrm{span}(\Lambda)$ 为该格张成的空间；记向量 $\bm{x} \in \mathrm{span}(\Lambda)$ ，对所有格向量 $\forall \bm{v} \in \Lambda$ ， $\bm{x}$ 满足 $\langle \bm{x}, \bm{y} \rangle \in \mathbb{Z}$ ；所有可能的 $\bm{x}$ 构成 $\Lambda$ 的对偶格 $\Lambda^\vee$ 。

张成的定义可以参考线性代数——线性组合、张成的空间与基。

以下图为例，它是一个整数格， $(\mathbb{Z}^n)^\vee = \mathbb{Z}^n$ 。其中，黑色点为原来的格点，红色点为对应的对偶格点。

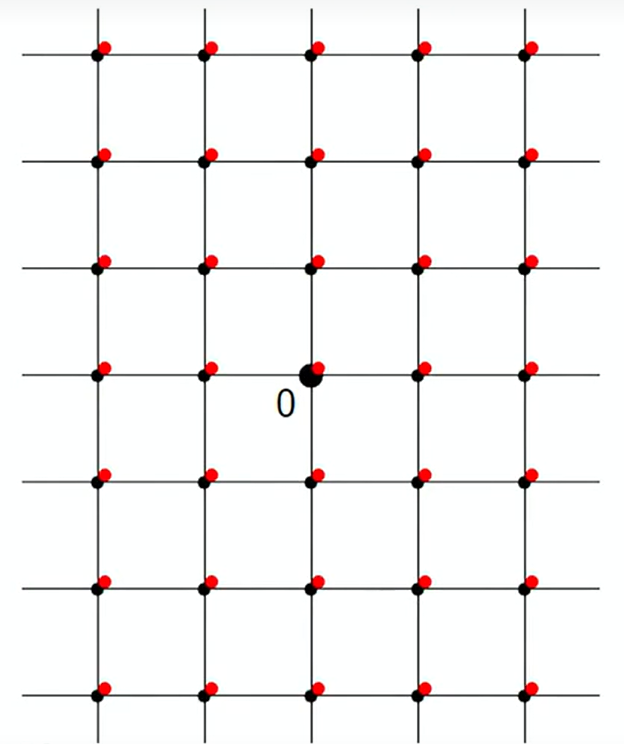
在这里插入图片描述

若对整数格加一个旋转，其对偶格为 $(\bm{R} \Lambda)^\vee = \bm{R}(\Lambda^\vee)$ 。原因：一个格向量发生了旋转，那么对偶格向量也必须旋转相同角度，才能保证向量乘积不变。

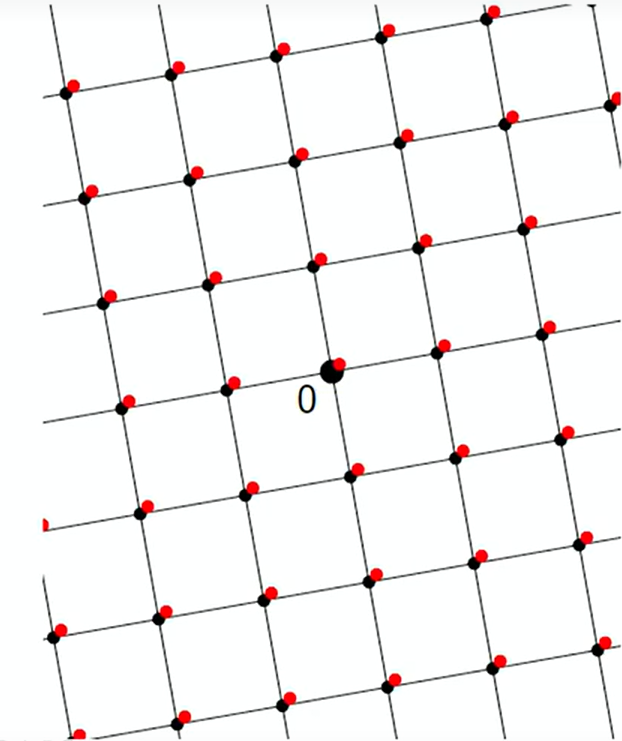
在这里插入图片描述

如果对格进行伸展，那么 $\cdot \Lambda)^\vee = \frac{1}{q} \cdot \Lambda^\vee$ 。

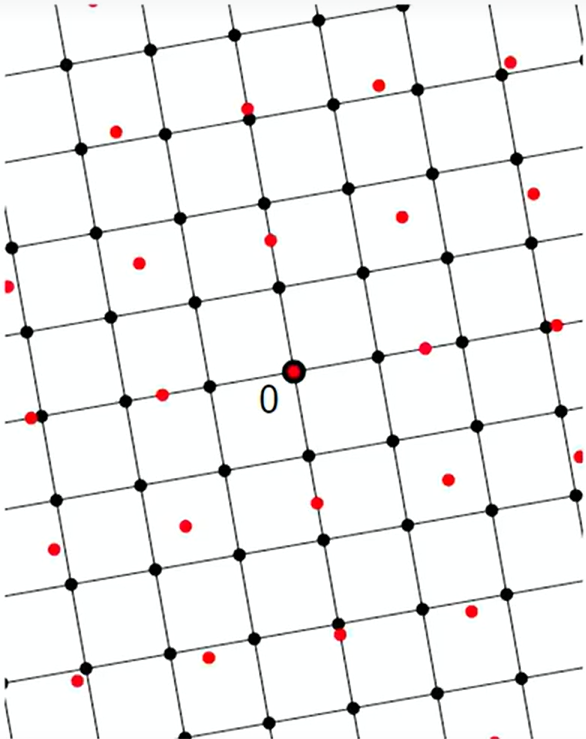
在这里插入图片描述

格与对偶格之间有一些基本属性关系，如：

$\Lambda_1 \subseteq \Lambda_2 \Leftrightarrow \Lambda_1^\vee \supseteq \Lambda_2^\vee$
$(\Lambda^\vee)^\vee = \Lambda$

整数格的对偶格比较好理解。但对于其它格，它们的对偶格看起来非常“混乱”，与原来的格没有太大的几何关系。例如，如果在原来的格上添加新的格点，由于定义中的约束关系： $\bm{x} \in \Lambda, \bm{y} \in \Lambda^\vee, \langle \bm{x}, \bm{y} \rangle \in \mathbb{Z}$ ，对偶格中的格点可能会减少。

在学习时，最好是把对偶格中每一个向量理解成一个“线性变换函数“，而不是一个几何意义上的格点。 仅需牢记 $\langle \bm{x}, \bm{y} \rangle \in \mathbb{Z}$ 即可，即格点和线性变换函数之间的运算。

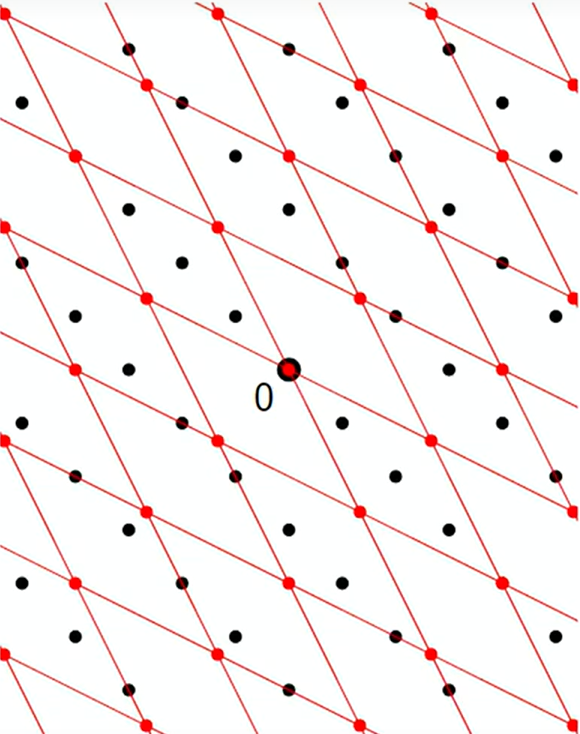
在这里插入图片描述

格分层

对偶格 $\mathcal{L}^\vee$ 中的每个向量 $\bm{v} \in \mathcal{L}^\vee$ 都能将格 $\mathcal{L}$ 分割成诸多个正交于 $\bm{v}$ 的层。具体而言，选定对偶格中的一个点 $\bm{v} \in \mathcal{L}^\vee$ ，然后让原本格中的所有点都与这个点相乘，把所有得到相同结果的格点都归为一层 $L_i$ ，即 $L_i = \{ \bm{x} \in \mathcal{L} : \bm{x} \cdot \bm{v} = i \}$ 。

以下图为例，黑色点为原来的格点，红色点为对应的对偶格点。

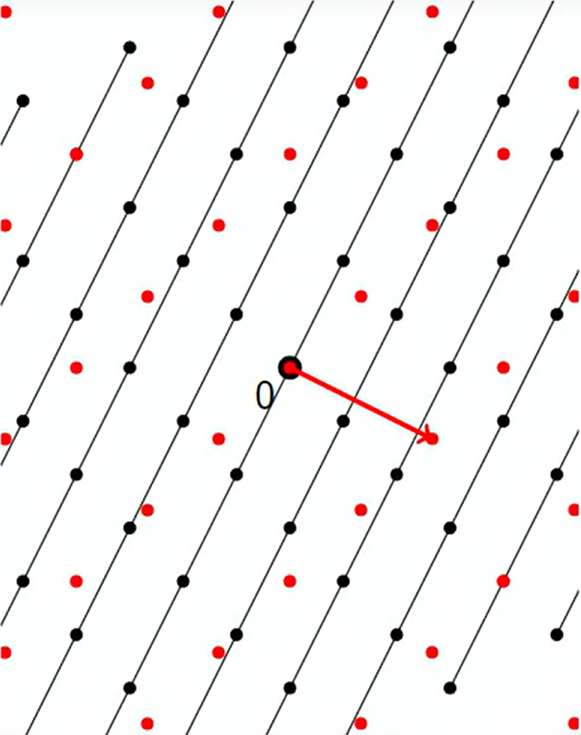
在这里插入图片描述

取不同对偶向量会有不同划分法，层与层之间的距离与所选对偶向量的长度成反比，即 $\mathrm{Dist}(L_i, L_{i+1}) = \frac{1}{\| \bm{v} \|}$ 。

在这里插入图片描述

注意：层与层之间不包含格点。 如果在两个分层之间放置一个超球体，这个超球体也不会包含任何格点，可以用来逼近原有格覆盖半径的下界，即 $\mu(\mathcal{L}) \geq \frac{1}{2 \| \bm{v} \|}$ 。

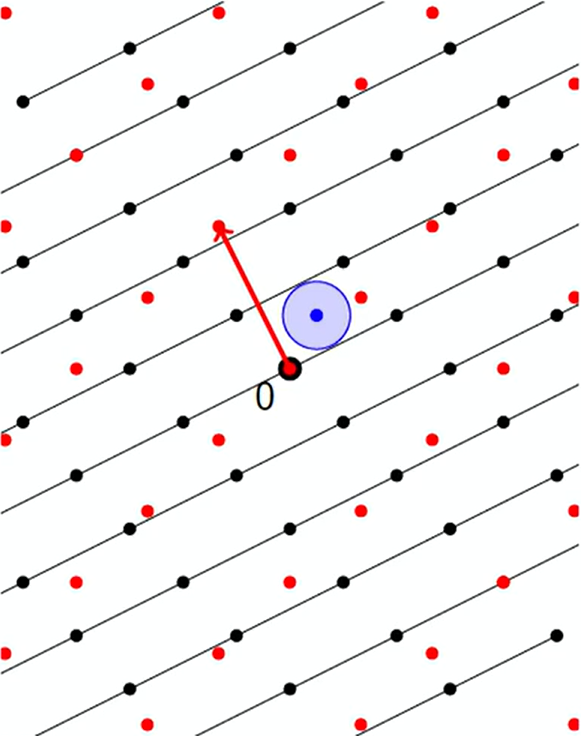
在这里插入图片描述

如果对偶格的 $\lambda_1(\mathcal{L}^\vee)$ 很小，那么原有格的覆盖半径 $\mu(\mathcal{L})$ 会很大。

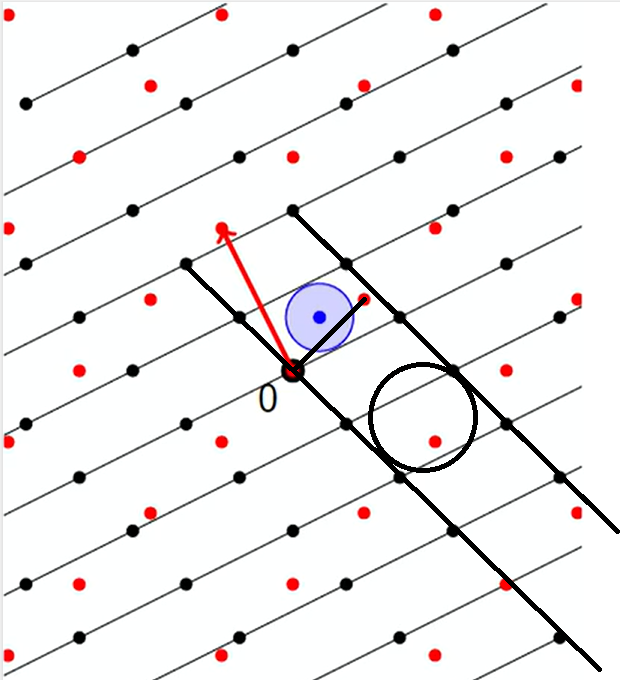
在这里插入图片描述

Banaszczyk定理

定理1 对于任意格 $\mathcal{L}$ ，有 $\leq 2\lambda_1(\mathcal{L}) \cdot \mu(\mathcal{L}^\vee) \leq n$ 。

定理2 对于任意 $i$ ，有 $\leq \lambda_i(\mathcal{L}) \cdot \lambda_{n-i+1}(\mathcal{L}^\vee) \leq n$ 。

BDD问题规约至SIVP问题上

下图简要给出了如何将BDD问题规约到SIVP问题上。个人疑问：为什么要选取SIVP问题的解？ 推测是因为层间距离与 $\| \bm{v}_i \|$ 成反比，若不是挑选最短的基向量而是很长的向量的话，那么格划分的层数会非常多，导致计算复杂度极高。

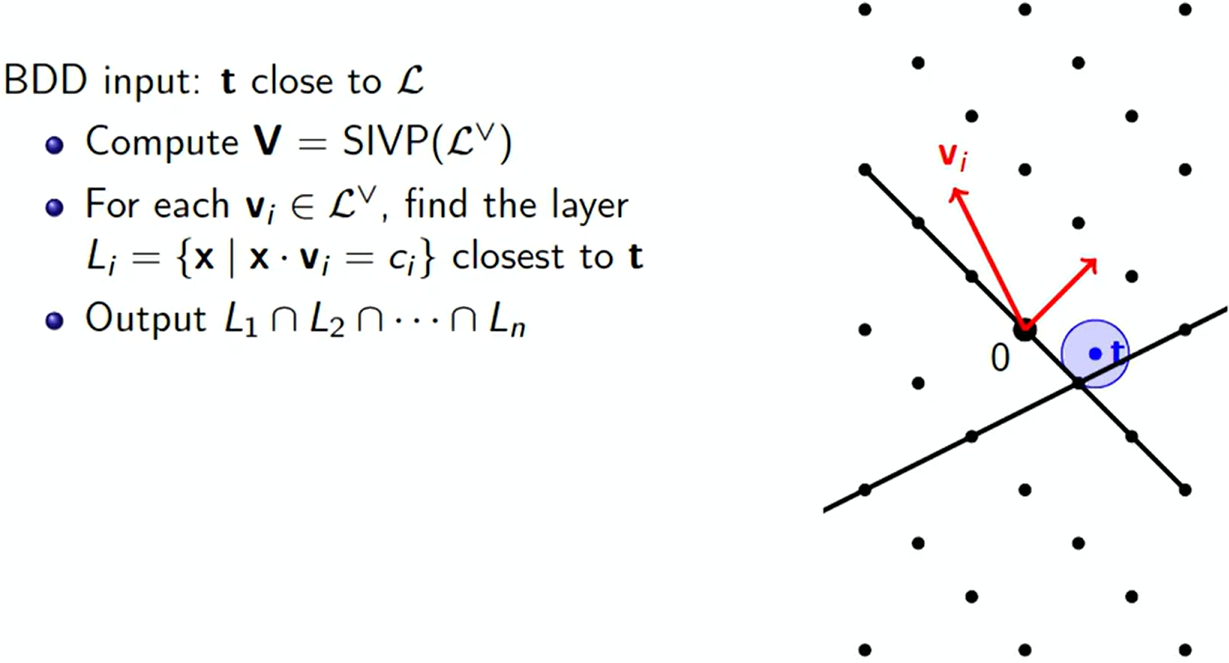
在这里插入图片描述

这个算法以较大概率求解出BDD问题的解。如何判断这个概率呢？当满足 $\mu(\bm{t}, \mathcal{L}) \leq \frac{\lambda_1}{2n} \leq \frac{1}{2\lambda_n^\vee} \leq \frac{1}{2 \| \bm{v}_i \|}$ 时，算法输出的解为正确解。