自适应核回归算法讲解

该文是对07年论文“Kernel Regression for Image Processing and Reconstruction”的总结性介绍。程序源码可从http://alumni.soe.ucsc.edu/~htakeda/KernelToolBox.htm下载。

对于初学者来说，首先要搞明白“核回归”是什么意思。所谓“回归”可以简单地理解为对样本值的拟合。在目标函数中，通常会给不同样本值误差分配不同的权重，决定权重分配的函数即为核函数，则便是“核回归”中“核”字的由来。比如在图像处理中，在对以当前点为中心的窗口内像素值进行拟合时，越靠近当前点的像素点往往被分配越高的权重，而远离当前点的像素点则被分配更低的权重。

先来考虑一维的情况。对于一个N阶局部光滑的一维函数来说，如果邻近，则有如下N阶泰勒展开式：

即邻域中所有样本点都可以用同一个常数项为当前点采样值（实际可能并未在该点采样）的多项式函数拟合，对邻域样本值进行多项式回归即可对当前点样本值进行重建或者说估计。由于这种重建只需要用于回归计算的样本在当前样本的邻域内，并不要求样本是均匀采样的，所以这种方法同样可以用来处理非均匀采样的重建。由于回归函数的N阶局部光滑性，这种回归重建具有平滑噪声的效果。

二维的情况与一维类似，只是这时的展开式是个二元多项式：

其中，，、含义如下：

vech(·)是半向量化算子，即：

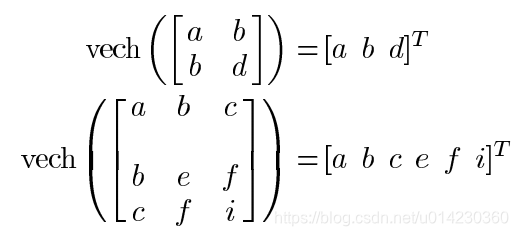
则最小二乘优化问题变成了：

其中，

 

是一个反映各采样点权重的对角矩阵：

对目标函数求导，令其等于0，可得:

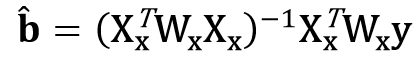
保留第一行，得：

常规的核函数是各项同性的，我们希望它能根据图像特征自适应调整，即，我们希望沿着边缘切线方向的权重更大，而沿边缘法线方向更小，如下图所示（其中(a)为经典核函数图示，(b)为自适应核函数图示）：

 

要实现图示中的变换，其实只需要构造一个代表的椭圆长轴方向与边缘法线方向（注意是法线！）一致的正定二次型作为距离度量矩阵即可。由于椭圆长短轴的大小意味着对应方向上的单位长度，切线方向对应短轴意味着切线方向的距离度量会被相对拉伸，对应权重越小（距离度量被用来指导高斯函数的sigma）；而法线方向对应长轴意味着法线方向的距离度量会被相对压缩，对应权重更大，这样就形成了权重沿切线方向分布的结果。而边缘强度越强，单位长度越大，距离度量越小，两个方向上高斯函数的simga越小，反之则越大。这样，对平滑区域则滤波半径越大，对纹理区域则滤波半径越小，也就实现了滤波核半径的自适应调整。指向性核函数（steering kernel）形如下式：

其中，度量矩阵作用于距离向量上实现了距离变换。

根据前面的分析，真正要解决的也就两个问题，一个是边缘方向估计的问题，一个是正定二次型度量矩阵的构造问题。

在边缘方向估计上，直接用单点梯度方向鲁棒性太差，且不能反映邻域整体的方向性。一个简单的想法就是用窗口内两方向梯度的协方差来反映局部方向（下式中和分别是沿和方向的一阶导，是当前点的局部分析窗口）：

这里对梯度协方差矩阵的含义做一个解读。梯度协方差矩阵是一个二次型，可以将其想成一个椭圆。首先考虑其为对角阵的简单情况，此时两方向梯度完全无关，此时边缘方向与梯度的计算方向一致，即为水平或竖直方向。其中，长轴对应对角线上较小的元素，也就是说长轴对应梯度值较小的方向，也就是边缘的切线方向。当边缘方向并非水平或垂直方向时，将水平与垂直方向梯度沿边缘切线与法线方向分解，会发现分解矩阵是一个旋转矩阵，也就是说，边缘方向的改变所带来的效果无非就是在原本由水平与垂直梯度组成的梯度向量上作用了一个旋转矩阵而已，而这个旋转角就是边缘切线方向与水平或者垂直方向的夹角。这种坐标系的旋转导致原来轴对称的椭圆旋转了一个角度，成为一个方向倾斜的椭圆，而这个新椭圆的长轴方向对应了边缘切线方向，椭圆的长轴大小对应了切线方向梯度值的倒数，短轴大小对应了法线方向梯度值的倒数。对协方差矩阵进行SVD分解，调节特征值大小即可调节椭圆长短轴长度和比例，控制权重核的形状。

论文中并没有使用梯度协方差矩阵，而是使用了梯度矩阵来确定边缘方向（协方差矩阵可以使用积分图加快计算，效率也许更高）。形式如下：

对进行特征值分解，有，

我们知道，对一个矩阵进行SVD分解意味着给原来的样本特征向量（这里就是梯度向量）换了一个新坐标系，使样本的主特征在新坐标系下具有最高的可分性，上式中  就是将旧坐标系旋转到新坐标系的旋转矩阵。奇异值矩阵对角线上每个元素值对应新坐标系下该维度特征的方差，对应样本向量在新坐标系下的表达。而我们知道，沿边缘法线方向的梯度值最大，方差也最大。所以让特征向量具有最高可分性即意味着把坐标轴旋转到与边缘法线及切线方向一致。也就是说，给出了边缘方向信息，而对角线上每个元素则对应边缘法线及切线方向的梯度方差。梯度方差的比值可以近似看作梯度分量的比值。也就是说，和提供了边缘方向与强度的充分信息，足以用于构建距离度量矩阵。

说到的构造，我们也可以对它进行SVD分解，得到下面的结果：

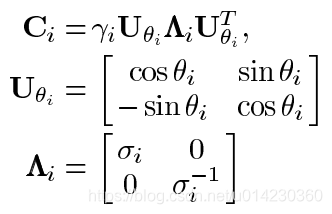
其中，控制坐标轴的长短（即单位长度），控制坐标轴的旋转，用以控制长短轴拉伸或压缩的比例，作用如下图所示：

在构造时，旋转矩阵当然还是使用，只需要对奇异值矩阵进行一下改造，根据奇异值控制一下长短轴长度及比例即可。具体的做法可以参见论文或自定义改造方法。

自适应核回归可以广泛用于上采样、图像去噪、图像修复、块效应去除等。算法可以迭代实施，每一次迭代都用上一次估计出来的的梯度信息重新估计方向构造距离度量矩阵，而像素值还使用原始图像的像素值。下面给出我随意从网上下载的一个低质量图像的处理效果：

原图

迭代3次处理的结果

可以看出，迭代3次效果已经很好了。事实上，迭代2次的结果与迭代3次的结果差异也非常小。不过由于在每个像素点都要进行SVD分解，所以程序计算量较大，比较耗时，并不适合实时处理，只适合追求质量的离线处理。

非均匀采样图像的恢复结果如下（采样率0.151）：

非均匀采样图像

重建结果​

重建操作不需要迭代实施，运行效果还是高了不少的。

算法的优化方向：

该算法原理上符合直觉，效果不错，主要缺点就是针对每个点都要求一个独特的权重矩阵W，进而导致复杂的矩阵运算，可以考虑把度量矩阵的三个决定性参数：长短轴比、旋转角度及缩放因子量化，预先计算出每一种组合下的权重矩阵其他相关的矩阵，待求得特征向量的两个奇异值后，直接查找对应的矩阵做最后的矩阵乘法运算即可。