深度学习用于医学预后-第二课第四周18-20节-使用Harrell C-Index评估生存模型

在本课程中，您将学习如何使用Harrell Concordance Index来评估生存模型的性能。

在之前，您已经计算过常规的Concordance Index（C-index）。现在您将学习当您处理生存数据时如何修改这个计算方法。这个最终工具将允许您评估您所学到的生存模型。

在本课中，我们将讨论使用Harrell C-Index评估生存模型的方法。我们已经看到了评估预后模型的设置。

之前我们在研究一个10年内死亡的风险，我们会为死亡率在10年内的结果是"是"或者"否"，并通过模型输出风险分数。我们发现C-Index，它考虑了成对比较，查看有多少对是一致的，有多少对是相等的（risk tie），并将其除以这些成对比较中的总对数。

对C-Index忘记了的同学，请点击下面链接回顾👇
C-Index

生存模型和我们之前看到的设置有两个主要的不同之处。第一个区别是我们关心建模的真实目标是事件时间，我们将其称为大写字母T。对于患者，我们有一个时间，例如30个月，表示患者的一个事件。第二个关键区别是我们的数据中有删失的观测数据，并且我们需要考虑如何在我们的评估中处理这些删失数据。

首先，让我们再次看看一致性(concordance)的概念。一致性是指最坏结果的患者应该具有较高的风险分数。

现在我们可以思考一下时间到事件的问题，更坏的结果意味着什么？

我们可以看到，如果一个患者早期发生了事件，那么他的结果将更坏。例如，左边患者在20个月时发生了事件，而右边患者在40个月时才发生事件，那么结果更糟糕的是生存时间更短的患者，因此我们应该为这个左边患者分配更高的风险分数。

因此，上图是成对一致的，因为它遵循了这个规则。

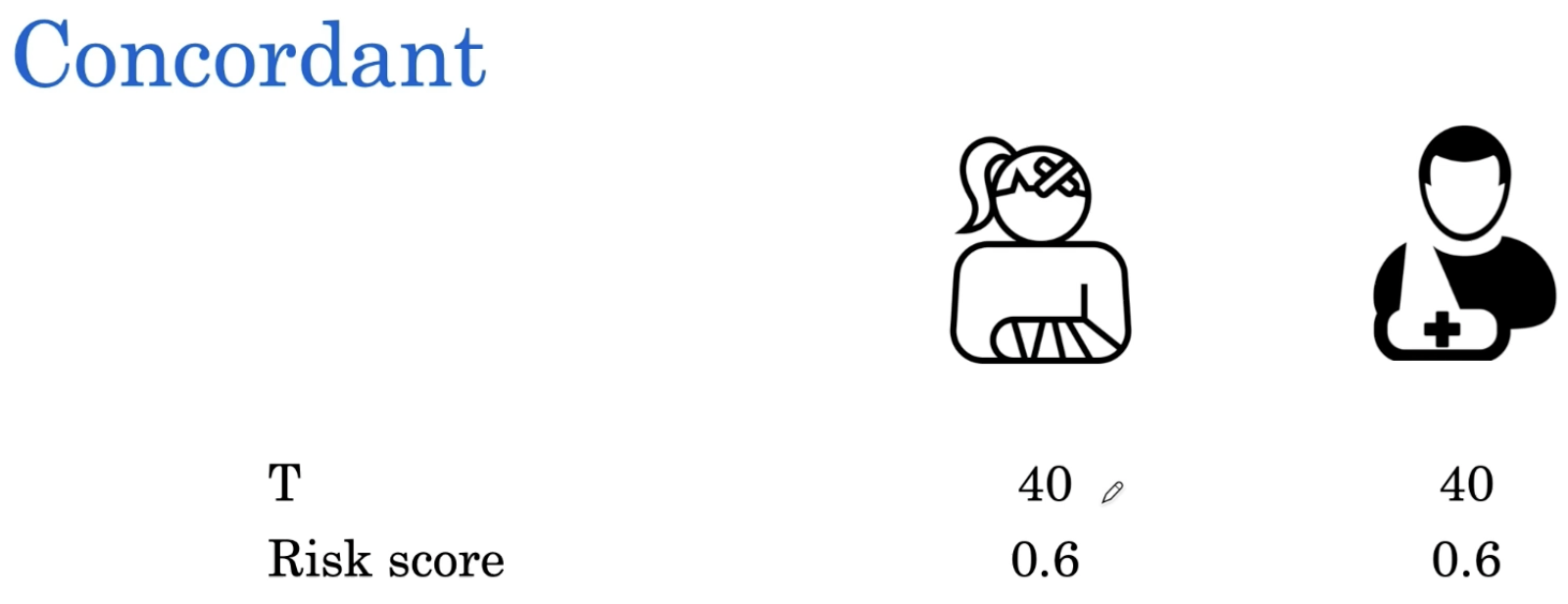
现在当我们的时间相同时，我们希望理想的风险分数表明两个人的风险是相同的。因此这又是一个一致的案例。

假设我们有两个不同的时间到事件，但更糟糕的结果得到了较低的风险分数这就是不一致(not concordant)。

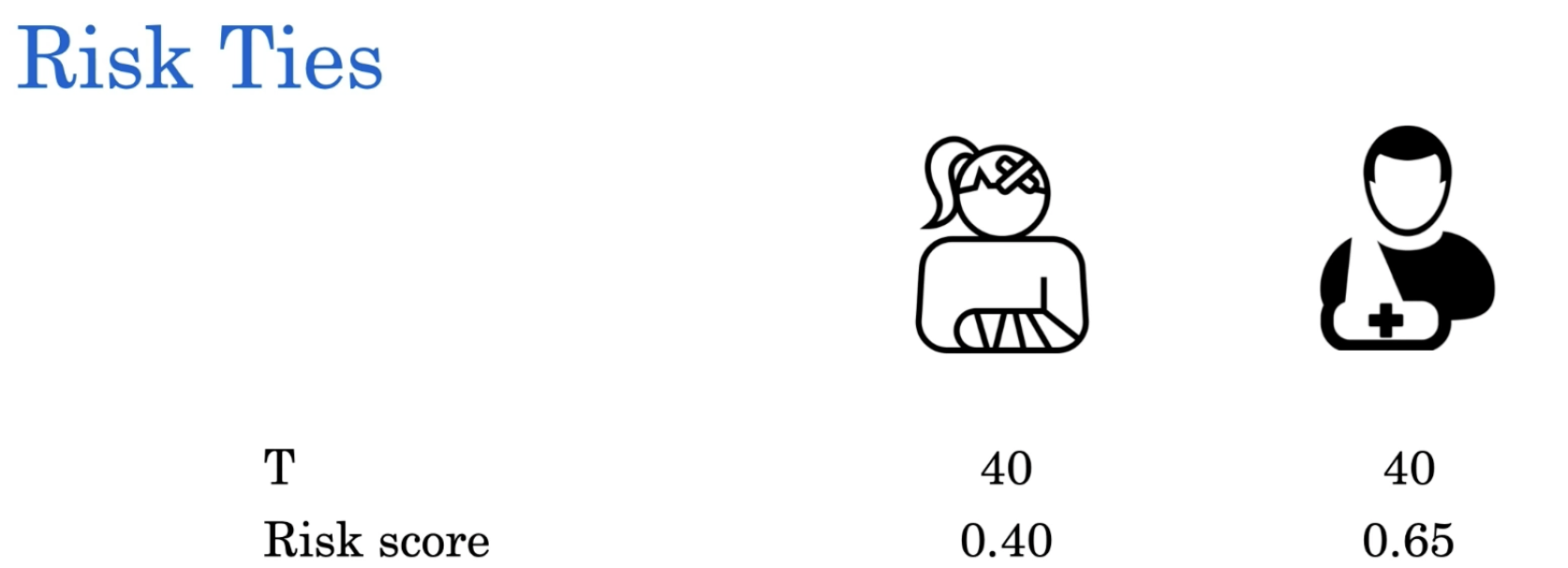
这是另一个风险类型的例子，其中我们有两个不同的时间到事件，但是我们有相同的风险分数。如果我们有两个病人的风险分数相同，但是他们的时间到事件不同，这将是一种风险平局(risk tie)的例子。

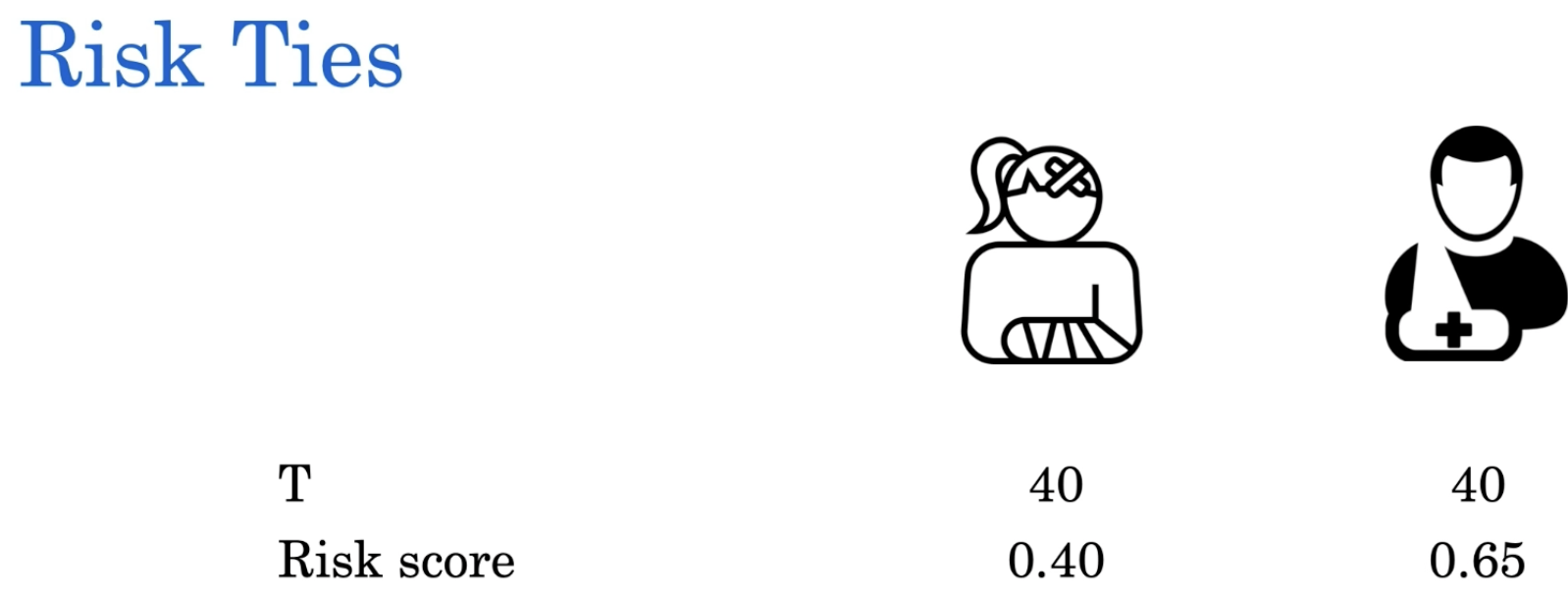
这也是一个风险平局的例子，其中我们有两个患者的时间到达事件相同，而我们说其中一个患者的风险分数小于其他患者。理想情况下，我们应该具有相同的风险分数，但它也不完全错误。所以我们将其称为risk tie。

允许和不允许配对

如果时间相同，风险不同，我们认为这是一个可允许对(permissible pairs)。

让我们看下面这个例子。有我们的第一个被删失的观测值，这是40+。因此，我们知道在40岁之前，这个患者没有经历任何事件，但他们之后又发生了事件。所以现在我们真的可以比较谁在这里的结果最差吗？

结果证明患者A显然有最坏的结果，因为右边比左边活得长，即使我们没有看到他们是否发生了事件，如果他们有任何事件，我们知道他们的结果肯定更好。

现在左边是被删失了，这种情况下我们是无法进行比较的。因此是不允许配对

两个数据都删失了，也是不允许配对的，不管删失的时间是不是相同。

那总结一下，哪些情况是允许配对的呢？

可能的允许配对

这一节就不废话了，直接看图中的情况，实心点表示有时间发生，空圈表示删失。线的长度代表时间。

不清楚的，可以看上面的例子。

最后，我们最后的Harrell C-Index公式👇

文章持续更新，可以关注微信公众号【医学图像人工智能实战营】获取最新动态，一个关注于医学图像处理领域前沿科技的公众号。坚持已实践为主，手把手带你做项目，打比赛，写论文。凡原创文章皆提供理论讲解，实验代码，实验数据。只有实践才能成长的更快，关注我们，一起学习进步~

我是Tina, 我们下篇博客见~

白天工作晚上写文，呕心沥血

觉得写的不错的话最后，求点赞，评论，收藏。或者一键三连