离散数学（十一）：关系的概念、表示和运算

0 前言

这一章 的题目是二元关系与函数。如何理解？ 函数，是x 到y 的映射，这种映射反应的就是一种关系（涉及到了x、y两个变量，所以是二元关系），因为定义域x 是一个集合、值域y 也是一个集合所以函数就是一个<x, y> 有序对的集合！

所以函数即是数对的集合！

函数的最基本定义不再是一种“对应规则”，而是集合。 有了函数的定义，我们就可以用 关系 来定义函数的复合、反函数 等概念。

此外，我们常常讲关系数据库，一个关系实际对应到一张关系数据表，作为数据库操作的数学基础，关系中不同的运算可映射到数据库中的不同操作。

1 有序对与笛卡尔积

1.1 有序对

定义： 由两个客体 x 和 y，按照一定的顺序组成的二元组称为有序对，记作<x,y>

实例：点的直角坐标(3,-4)

性质:   有序性  <x,y><y,x> （当xy时） 

例1  <2, x+5> = <3y- 4, y>，求 x, y.

解     3y- 4 = 2, x+5 = y   y = 2, x = - 3  

1.2 笛卡尔积

定义   设A,B为集合，A与B 的笛卡儿积记作AXB， 即       A X B ={ <x,y> | xA   yB }

例2  A={1,2,3}, B={a,b,c}

 AXB ={<1,a>,<1,b>,<1,c>,<2,a>,<2,b>,<2,c>, <3,a>,<3,b>,<3,c>}

 BXA ={<a,1>,<b,1>,<c,1>,<a,2>,<b,2>,<c,2>, <a,3>, <b,3>,<c,3>}

   

1.3 笛卡尔积的性质

 

2 关系

2.1 二元关系 

定义 如果一个集合满足以下条件之一, 则称该集合为一个二元关系, 简称为关系，记作R.

（1）集合非空, 且它的元素都是有序对

（2）集合是空集

如<x,y>∈R, 可记作 xRy； 

实例：R={<1,2>,<a,b>}, S={<1,2>,a,b}.

R是二元关系, 当a, b不是有序对时，S不是二元关系

2.2 A上的二元关系 

定义 设A,B为集合,  A×B的任何子集所定义的二元关系叫做从A到B的二元关系,

当A=B时则叫做 A上的二元关系.

例4  A={0,1}, B={1,2,3},  R1={<0,2>},  R2=A×B,  R3={<0,1>}. 那么 R1, R2, R3 是从 A 到 B

的二元关系, R3 也是 A上的二元关系.

计数：|A|=n, |A×A|=n2, A×A的子集有 个. 所以 A上有 个不同的二元关系.

例如 |A|=3, 则 A上有=512个不同的二元关系.

2.3 关系举例

空关系：设 A 为任意集合，是 A 上的关系，称为空关系.

全域关系:  ={<x,y>|x∈A∧y∈A}=A×A
恒等关系:  ={<x,x>|x∈A}

 小于等于关系: 

 整除关系:  

包含关系:
例如, A={1,2}, 则
 EA={<1,1>,<1,2>,<2,1>,<2,2>}
 IA={<1,1>,<2,2>}

 2.4 关系的表示

关系的表示方式有三种：关系的集合表达式、关系矩阵、关系图。

• 关系集合：
• 关系矩阵：若A={a1, a2, …, am}，B={b1, b2, …, bn}，R是从A到B的关系，R的关系矩阵是布尔矩阵
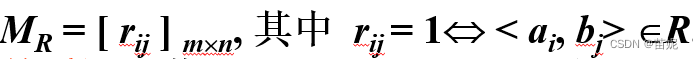
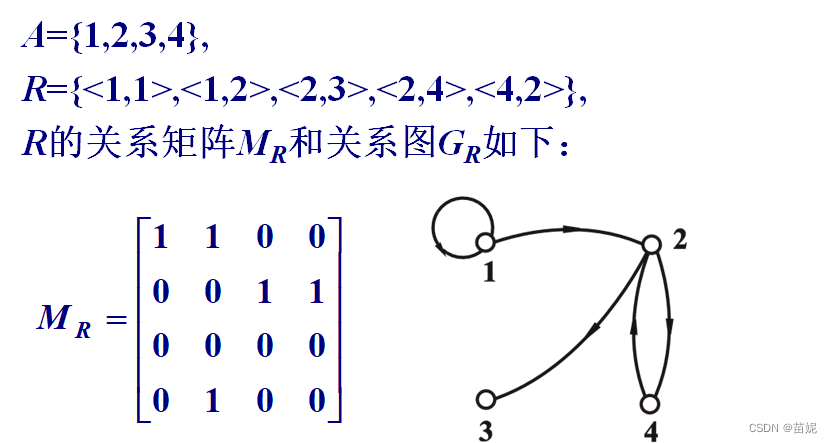
• 关系图：若A= {x1, x2, …, xm}，R是从A上的关系，R的关系图是GR=<A, R>, 其中A为结点集，R为边集.如果<xi,xj>属于关系R，在图中就有一条从 xi 到 xj 的有向边.

注意：A, B为有穷集，关系矩阵适于表示从A到B的关系或者A上的关系，关系图适于表示A上的关系。

 3 关系的运算