目录
波动方程数值解是波动方程正演、逆时偏移和全波形反演的核心技术之一。本文采用二阶有限差分对波动方程进行了离散，进而实现了对波动方程的数值求解，模拟出其在介质中的传播过程。
NumPy 通常与 SciPy（Scientific Python）和 Matplotlib（绘图库）一起使用， 这种组合广泛用于替代 MatLab，是一个强大的科学计算环境，有助于我们通过 Python 学习数据科学或者机器学习。
SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包，如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口（API）。
本文代码部分才用了 NumPy和Matplotlib包。
1、原理：
1）二维声波波动方程:
其中u 为声压，f 为震源中心声压，x/z 为x/z 方向的采样点，t 为时间，v 为速度。
利用泰勒公式对进行展开得到：
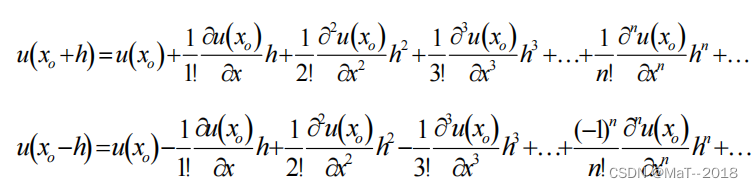
两式相加得：
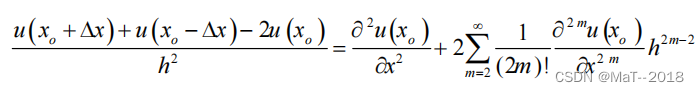
则有：
近似得二阶差分算子：
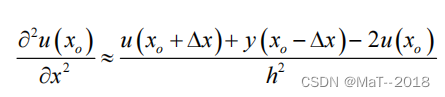
利用二阶中心差分算子对二阶导数进行离散：
将上式代入声波方程得到二阶中心差分格式：
其空间和时间差分格式示意图如下图所示：
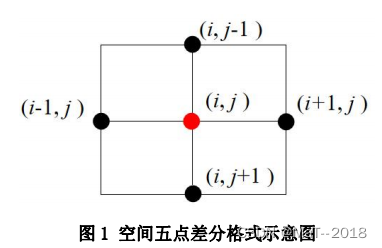
2）收敛条件（不是很明白）
3）雷克子波
雷克子波是地震子波中的一种。由震源激发、经地下传播并被人们在地面或井中接收到的地震波通常是一个短的脉冲振动，称该振动为振动子波， 如下图所示。
公式为： f(t)=(1-2*(pi*f*t)^2)*exp(-(pi*f*t)^2) ，其中t 为时间，f 为主频。
4）二维空间衰减函数
震源中心为1，不衰减，距离中心越远，衰减程度越大。
h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数
下图显示的是h_x_z[150] 的曲线，整个的二维空间衰减系数h_x_z，以[150,150] 为中心（震源），向四周衰减。
5）边界吸收条件 (不是很明白。。)
作用：声波传播时是没有边界的，因此也不存在边界反射问题。但由于模拟正演时，观测范围有限，因此必然是有边界的，边界吸收条件就是尽可能的将能量吸收，将边界反射降到最低。（我的理解哈，欢迎讨论）以下是两种边界吸收条件。现在用的比较多的是PML条件。
Clayton-Engquist 单成波吸收边界条件: 最早是由 Clayton 等人发现并推广的， 其微分表达式为：
其中：n 为边界的外法线方向； s 边界的切线方向。
对上式进行离散得到上、下、左、右边界差分格式如下：
其中：N 、 M 为边界的网格数。
Reynolds 边界条件：对于二维声波波动方程，应用二维声波方的微分算子可以，得到：
对上式进行离散可得上下左右边界计算公式：
2、编程实现
1）参数设置：
- x/z方向长度1500m，x/z方向空间步长5m，每个方向的采样点数为301；
- 模拟时长1s，时间步长0.001s，时间采样数1000；
- 震源频率25Hz；
- 空间衰减因子0.5；
- 波速固定，任何位置都为3000m/s
- 震源位置在中心；初始声压为0。
# 区域大小
Nx = 301
Nz = 301
# 空间间隔
dx = h
dy = h
# 时间采样数
Nt = 1000
# 时间步
dt = 1 / Nt
# 速度模型
v = np.ones((Nx+1,Nz+1)) * 3000
u = np.zeros((Nt+1,Nx+1,Nz+1))
h = 5
# 子波主频
fm = 25
# 空间衰减因子
alpha = 0.5
# 迭代公式中的r
A = v **2 * dt ** 2 / h ** 2
C = v * dt / h
2）雷克子波及二维空间衰减函数
t = np.arange(0, Nt+1)
t0 = 0 # 延迟时间，相当于在t=t0时激发 ，震幅在t0时最大，相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)
x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)
h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数
x0 = Nx // 2
z0 = Nz // 2
u0 = lambda r, s: 0.25*np.exp(-((r-x0)**2+(s-z0)**2))
JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)
3）边界吸收条件
# 边界条件
ii = np.arange(Nx+1)
jj = np.arange(Nz+1)
# Clayton-Engquist-majda 二阶吸收边界条件
u[t+1, 0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t, 0, jj] \
+ 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t, 1, jj] \
- C[ 2, jj] ** 2 * u[t, 2, jj] \
+ (2 * C[ 0, jj] - 1) * u[t - 1, 0, jj] \
- 2 * C[ 1, jj] * u[t - 1, 1, jj]
# 下部
u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t, -1, jj] \
+ 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t, -2, jj] \
- C[ -3, jj] ** 2 * u[t, -3, jj] \
+ (2 * C[ -1, jj] - 1) * u[t - 1, -1, jj] \
- 2 * C[ -2, jj] * u[t - 1, -2, jj]
# 左部
u[t+1, ii, 0] = (2 - 2 * C[ii, 0] - C[ii, 0] ** 2) * u[t, ii, 0] \
+ 2 * C[ii, 1] * (1 + C[ii, 1]) * u[t, ii, 1] \
- C[ii, 2] ** 2 * u[t, ii, 2] \
+ (2 * C[ii, 0] - 1) * u[t - 1, ii, 0] \
- 2 * C[ii, 1] * u[t - 1, ii, 1]
# 右部
u[t+1, ii, -1] = (2 - 2 * C[ii, -1] - C[ii, -1] ** 2) * u[t, ii, -1] \
+ 2 * C[ii, -2] * (1 + C[ii, -2]) * u[t, ii, -2] \
- C[ii, -3] ** 2 * u[t, ii, -3] \
+ (2 * C[ii, -1] - 1) * u[t - 1, ii, -1] \
- 2 * C[ii, -2] * u[t - 1, ii, -2]
#Reynolds 边界条件
u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]
u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]
u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]
u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]
4）波动方程，迭代公式：
# 迭代公式
u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]
5）全部代码如下：
import numpy as np
import imageio
import os
import pandas as pd
from matplotlib import pyplot as plt
# 解决中文问题
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
Nx = 301
Nz = 301
Nt = 1000
v = np.ones((Nx+1,Nz+1)) * 3000
h = 5
fm = 25
alpha = 0.5
dt = 1 / Nt
dx = h
dy = h
A = v **2 * dt ** 2 / h ** 2
C = v * dt / h
r = np.max(v)*dt/h
assert r < 0.707,f'r should < 0.707, but is {r}'
u = np.zeros((Nt+1,Nx+1,Nz+1))
t = np.arange(0, Nt+1)
t0 = 0 # 延迟时间，相当于在t=t0时激发 ，震幅在t0时最大，相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)
plt.plot(s_t)
plt.show()
x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)
# print(((z - Nz//2)**2).shape)
h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数
JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)
mode = 'c_e'
img_path = './2_order'
if not os.path.exists(img_path):
os.makedirs(img_path)
for t in range(2,Nt):
print('\rstep {} / {}'.format(t ,Nt), end="")
# 边界条件
ii = np.arange(Nx+1)
jj = np.arange(Nz+1)
if mode == 'c_e':
# Clayton-Engquist-majda 二阶吸收边界条件
u[t+1, 0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t, 0, jj] \
+ 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t, 1, jj] \
- C[ 2, jj] ** 2 * u[t, 2, jj] \
+ (2 * C[ 0, jj] - 1) * u[t - 1, 0, jj] \
- 2 * C[ 1, jj] * u[t - 1, 1, jj]
# 下部
u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t, -1, jj] \
+ 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t, -2, jj] \
- C[ -3, jj] ** 2 * u[t, -3, jj] \
+ (2 * C[ -1, jj] - 1) * u[t - 1, -1, jj] \
- 2 * C[ -2, jj] * u[t - 1, -2, jj]
# 左部
u[t+1, ii, 0] = (2 - 2 * C[ii, 0] - C[ii, 0] ** 2) * u[t, ii, 0] \
+ 2 * C[ii, 1] * (1 + C[ii, 1]) * u[t, ii, 1] \
- C[ii, 2] ** 2 * u[t, ii, 2] \
+ (2 * C[ii, 0] - 1) * u[t - 1, ii, 0] \
- 2 * C[ii, 1] * u[t - 1, ii, 1]
# 右部
u[t+1, ii, -1] = (2 - 2 * C[ii, -1] - C[ii, -1] ** 2) * u[t, ii, -1] \
+ 2 * C[ii, -2] * (1 + C[ii, -2]) * u[t, ii, -2] \
- C[ii, -3] ** 2 * u[t, ii, -3] \
+ (2 * C[ii, -1] - 1) * u[t - 1, ii, -1] \
- 2 * C[ii, -2] * u[t - 1, ii, -2]
if mode == 're':
#Reynolds 边界条件
u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]
u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]
u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]
u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]
# 迭代公式
u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]*v[II, JJ]**2*dt**2+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]
plt.imshow(u[t], cmap='gray_r') # 'seismic' gray_r
# plt.axis('off') # 隐藏坐标轴
plt.colorbar()
if t % 10 == 0:
plt.savefig(os.path.join(img_path, str(t) + '.png'),
bbox_inches="tight", # 去除坐标轴占用空间
pad_inches=0.0) # 去除所有白边
plt.pause(0.05)
plt.cla()
plt.clf() # 清除所有轴，但是窗口打开，这样它可以被重复使用
plt.close()
# 保存gif
filenames=[]
for files in os.listdir(img_path ):
if files.endswith('jpg') or files.endswith('jpeg') or files.endswith('png'):
file=os.path.join(img_path ,files)
filenames.append(file)
images = []
for filename in filenames:
images.append(imageio.imread(filename))
imageio.mimsave(os.path.join(img_path, 'wave.gif'), images,duration=0.0001)
参考：
波动方程数值求解（一）_声波方程的解_MaT--2018的博客-CSDN博客
3、基于matlab的二维波动方程实现
close all
clear
clc
% 此程序是有限差分法实现声波方程数值模拟
%% 参数设置
delta_t = 0.001; % s
delta_s = 10; % 空间差分：delta_s = delta_x = delta_y (m)
nx = 800;
ny = 800;
nt = 1000;
fmain = 12.5;
%loop:按照10000s为一次大循环；slice代表每隔1000s做一个切片
loop_num = 3;
slice = 1000;
slice_index = 1;
%% 初始化
%震源
t = 1:nt;
t0 = 50;
s_t = (1-2*(pi*fmain*delta_t*(t-t0)).^2).*exp(-(pi*fmain*delta_t*(t-t0)).^2);%源
%一个loop代表向后计算10000s,目的是减少内存消耗
%间隔1000s保存一张切片
num_slice = nt*loop_num/slice;
U_loop(1:ny,1:nx,1:num_slice) = 0;
U_next_loop(1:ny,1:nx,1:2) = 0;
%初始化数组变量
w(1:ny,1:nx) = 0;
U(1:ny,1:nx,1:nt) = 0;
w(400,400) = 1;
V(1:ny,1:nx) = 2000;
A = V.^2*delta_t^2/delta_s^2;
B = V*delta_t/delta_s;
%% 开始计算
JJ = 2:ny-1;
II = 2:nx-1;
start_time = clock;
for loop = 1:loop_num
fprintf('Loop=%d\n',loop)
for i_t = 2:nt-1
if(loop>1)
s_t(i_t) = 0;
end
%上边界
U(1,II,i_t+1) = (2-2*B(1,II)-A(1,II)).*U(1,II,i_t)+2*B(1,II).*(1+B(1,II)).*U(2,II,i_t)...
-A(1,II).*U(3,II,i_t)+(2*B(1,II)-1).*U(1,II,i_t-1)-2*B(1,II).*U(2,II,i_t-1);
%下边界
U(ny,II,i_t+1) = (2-2*B(ny,II)-A(ny,II)).*U(ny,II,i_t)+2*B(ny,II).*(1+B(ny,II)).*U(ny-1,II,i_t)...
-A(ny,II).*U(ny-2,II,i_t)+(2*B(ny,II)-1).*U(ny,II,i_t-1)-2*B(1,II).*U(ny-1,II,i_t-1);
%左边界
U(JJ,1,i_t+1) = (2-2*B(JJ,1)-A(JJ,1)).*U(JJ,1,i_t)+2*B(JJ,1).*(1+B(JJ,1)).*U(JJ,1+1,i_t)...
-A(JJ,1).*U(JJ,1+2,i_t)+(2*B(JJ,1)-1).*U(JJ,1,i_t-1)-2*B(JJ,1).*U(JJ,1+1,i_t-1);
%右边界
U(JJ,nx,i_t+1) = (2-2*B(JJ,nx)-A(JJ,nx)).*U(JJ,nx,i_t)+2*B(JJ,nx).*(1+B(JJ,nx)).*U(JJ,nx-1,i_t)...
-A(JJ,nx).*U(JJ,nx-2,i_t)+(2*B(JJ,nx)-1).*U(JJ,nx,i_t-1)-2*B(JJ,nx).*U(JJ,nx-1,i_t-1);
%递推公式
U(JJ,II,i_t+1) = s_t(i_t).*w(JJ,II)+A(JJ,II).*(U(JJ,II+1,i_t)+U(JJ,II-1,i_t)+U(JJ+1,II,i_t)+U(JJ-1,II,i_t))+...
(2-4*A(JJ,II)).*U(JJ,II,i_t)-U(JJ,II,i_t-1);
if(mod(i_t,100)==0)
run_time = etime(clock,start_time);
fprintf('step=%d,total=%d,累计耗时%.2fs\n',i_t+(loop-1)*nt,nt*loop_num,run_time)
U_loop(:,:,slice_index) = U(:,:,i_t);
slice_index = slice_index +1;
end
end
%处理四个角点
KK = 1:nt;
U(1,1,KK) = 1/2*(U(1,2,KK)+U(2,1,KK));
U(1,nx,KK) = 1/2*(U(1,nx-1,KK)+U(2,nx,KK));
U(ny,1,KK) = 1/2*(U(ny-1,1,KK)+U(ny,2,KK));
U(ny,nx,KK) = 1/2*(U(ny-1,nx,KK)+U(ny,nx-1,KK));
%% 为下一次loop做准备
fprintf('step=%d,total=%d,累计耗时%.2fs\n',i_t+1+(loop-1)*nt,nt*loop_num,run_time)
U_loop(:,:,slice_index) = U(:,:,nt);
slice_index = slice_index +1;
U_next_loop(:,:,1)=U(:,:,nt-1);
U_next_loop(:,:,2)=U(:,:,nt);
U(:,:,:) = 0;
U(:,:,1) = U_next_loop(:,:,1);
U(:,:,2) = U_next_loop(:,:,2);
end
%% 制作动图
fmat=moviein(num_slice);
filename = 'FDM_4_homogenerous.gif';
for II = 1:num_slice
pcolor(U_loop(:,:,II));
shading interp;
axis tight;
set(gca,'yDir','reverse');
str_title = ['FDM-4-homogenerous t=',num2str(delta_t*II*100),'s'];
title(str_title)
drawnow; %刷新屏幕
F = getframe(gcf);%捕获图窗作为影片帧
I = frame2im(F); %返回图像数据
[I, map] = rgb2ind(I, 256); %将rgb转换成索引图像
if II == 1
imwrite(I,map, filename,'gif', 'Loopcount',inf,'DelayTime',0.1);
else
imwrite(I,map, filename,'gif','WriteMode','append','DelayTime',0.1);
end
fmat(:,II)=getframe;
end
movie(fmat,10,5);
%% 绘图为gif
pcolor(U_loop(:,:,num_slice))
shading interp;
axis tight;
set(gca,'yDir','reverse');
str_title = ['FDM-4-homogenerous t=',num2str(delta_t*num_slice*100),'s'];
title(str_title)
colormap('Gray')
filename = [str_title,'.jpg'];
saveas(gcf,filename)
%% 耗时
toc
1189
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
