一般情况下,最优化问题会有三类:
(一)、无约束条件
这种情况想都不用想,直接对变量求导等于0,代入原函数验证即可。
(二)、等式约束条件
我们假定目标函数为f(x),约束条件为h_k(x)。
minf(x)minf(x) (最大值最小值问题可以相互转化)
s.t. hk(x)=0,k=1,2,3...s.t. hk(x)=0,k=1,2,3...
我们原来高中学过的消元法不失为一种好方法,但是毕竟比较Low,体现不出优秀的你的水平哈哈,不开玩笑了,主要是消元的时候会很麻烦,比如说有高次的情况,开根号带来了计算时许多不便之处,而拉格朗日就厉害了,为什么这么讲呢,我们一起来看看:
拉格朗日乘子法的求解流程大概包括以下几个步骤:
1. 构造拉格朗日函数
2. 解变量的偏导方程
3. 代入目标函数即可
是不是看上去很简单,其实的确不麻烦(==,吐槽一下当时看向量机的时候,还一直纠结着看不懂,但其实本身这个方法并没有想象的那么难)。关键在于构造拉格朗日函数,后面求解实际上就是高数里面基本的求偏导数的问题了。我们不妨另:
F(x,λ)=f(x)+∑lk=1λkhk(x)F(x,λ)=f(x)+∑k=1lλkhk(x)
然后分别对每一个变量求导,得出来的解代入目标函数就ok了!
∂Fλk=0∂Fλk=0 ∂Fxi=0∂Fxi=0 …
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。
常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x),
KKT条件是说最优值必须满足以下条件:
1)L(a, b, x)对x求导为零;
2)h(x) =0;
3)a*g(x) = 0;










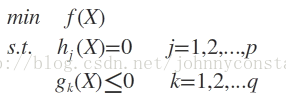
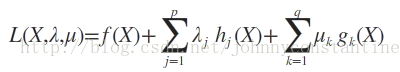














 1249
1249

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








