数学建模中热传导方程有限元法（FEM）的深度解析

数学建模中热传导方程有限元法（FEM）的深度解析与工程实践

一、引言：热传导问题的物理本质与数学建模

热传导是自然界中普遍存在的能量传递现象，其数学描述通过偏微分方程（PDE）实现。以三维非稳态热传导方程为例：

其中，T为温度场，k为热导率张量，ρ为密度，cp​为比热容，Q为内热源密度。该方程的求解需要结合三类边界条件：

传统解析方法仅适用于简单几何和均匀材料，而有限元法（FEM）通过离散化策略，能够处理复杂边界条件和材料各向异性问题。例如，在航空发动机叶片冷却分析中，叶片内部包含复杂随形冷却通道，传统方法难以精确建模，而FEM可通过非结构化网格实现高精度模拟

---

二、有限元法的基本原理与热传导问题适配性

2.1 FEM的核心思想与数学基础

有限元法的核心是通过变分原理将连续问题离散化。对于热传导方程，其弱形式可通过加权残值法推导：

应用格林公式后得到：

其中ψ为权函数，满足Galerkin法的ψ=Ni​（形函数）。这一过程将偏微分方程转化为代数方程组，其数学本质是能量泛函的极值问题

2.2 热传导问题的FEM适配性分析

优势维度	具体表现	典型应用场景
几何适应性	支持任意复杂几何建模（如随形冷却水道、多孔介质）	航空发动机热防护设计 1
材料特性处理	允许各向异性热导率（如碳纤维复合材料k_x≠k_y）	新能源电池热管理 4
多物理场耦合	可扩展至热-力耦合（如芯片热膨胀应力分析）	微电子器件可靠性评估 7
动态过程模拟	支持瞬态分析（如激光脉冲加热过程的温度波动）	焊接工艺优化 9

---

三、热传导方程FEM求解的完整流程

3.1 前处理阶段

3.1.1 网格生成策略

• ​结构化网格​：适用于规则几何（如平板导热），采用四边形/六面体单元，计算效率高
• ​自适应网格​：基于温度梯度场动态加密节点（如ICEM CFD的自适应功能），在热斑区域提升精度
• ​多尺度建模​：结合宏观网格（mm级）与微观网格（μm级），模拟多孔介质中的传热

​案例​：某芯片散热仿真中，采用混合网格策略，在芯片热点区域（<1mm²）使用20节点六面体单元，其余区域使用四面体单元，节点总数控制在50万以内

3.1.2 材料属性定义

热传导问题中需定义的参数包括：

• ​各向异性热导率​：如石墨烯层状结构的k_x=5000 W/(m·K), k_y=300 W/(m·K)
• ​温度依赖性​：采用Arrhenius模型描述高温下的热导率衰减
• ​相变材料​：引入潜热项L(T)，修正能量方程

3.2 单元分析核心步骤

3.2.1 弱形式推导与形函数选择

对于二维三角形单元，形函数满足：

其中系数由节点坐标确定。通过将温度场表示为T=∑Ni​Ti​，代入弱形式可得单元方程：

其中刚度矩阵元素：

3.2.2 单元刚度矩阵组装

以四边形单元为例，其刚度矩阵为：

组装时需注意节点编号的映射关系，避免重复计算

3.3 边界条件处理技术

3.3.1 Dirichlet边界条件

直接修改刚度矩阵和载荷向量：

• ​强施加​：将对应节点温度固定为T0​，令Kii​→∞
• ​弱施加​：通过罚函数法，添加106⋅(T−T0​)到载荷项

3.3.2 Neumann边界条件

对第二类边界条件，载荷向量修正为：

例如，表面散热条件下：

3.3.3 Robin边界条件

需同时修改刚度矩阵和载荷向量：

3.4 求解器选择与优化

求解器类型	适用场景	优缺点分析
直接法	中小规模问题（<10万节点）	精度高，但内存消耗大
共轭梯度法	对称正定矩阵	收敛速度慢，需预处理
GMRES	非对称矩阵	需存储完整Krylov子空间
多重网格法	大规模问题	收敛速度快，需实现平滑算子

​并行计算策略​：采用域分解法（Domain Decomposition），将全局网格划分为子域，各子域独立求解后通过Schwarz迭代修正边界条件。

四、工程案例深度解析

---

4.1 电子芯片瞬态热分析（7nm工艺）

​物理模型构建​
针对7nm制程芯片的瞬态热行为，建立三维瞬态热传导方程：

其中：

• ​材料参数​：硅热导率随温度变化（25℃时k=149 W/(m·K)，80℃时k=132 W/(m·K)）
• ​热源分布​：CMOS核心区瞬时功率密度达1000 W/cm²（脉冲宽度10μs）
• ​散热系统​：微流道冷却液（Pr=0.011，雷诺数Re=1200，流动为层流）

​网格优化策略​

• ​自适应四面体网格​：在功率晶体管区域（<10μm）采用20节点六面体单元，热边界层区域加密至5层
• ​多尺度耦合​：芯片级网格（1μm）与封装级网格（10μm）通过接口单元连接
• ​动态网格修正​：基于温度梯度场实时调整网格密度（ANSYS Meshing自适应算法）

​仿真设置详解​

参数	设置值	技术细节
时间步长	Δt=0.1ms（显式格式）	采用CFL条件自动调整（CFL=0.8）
求解器	UMFPACK直接法	预处理采用不完全LU分解（ILUT），容差1e-6
热载荷	阶梯脉冲加载	0-200s：5e7 W/m³；200-400s：0 W/m³
边界条件	微流道强制对流	Nu=0.023Re^0.8Pr^0.4，冷却液入口温度25℃

​结果深度解析​

1. ​温度场分布​

   • 最大温升ΔT=82.3℃（位于功率晶体管中心），热扩散时间常数τ=RC=3.2ms
   • 热脊线走向显示：热流沿金属互连层向四周扩散，形成"热岛效应"

2. ​瞬态响应分析​

   • 温度波动幅值：ΔT_max=15.7℃（脉冲峰值时刻）
   • 热滞后效应：功率关闭后温度衰减时间常数τ_decay=4.8ms

3. ​热失效评估​

   • 热应力集中：在焊球连接处产生320MPa热应力（硅屈服强度7GPa）
   • 疲劳寿命预测：基于Coffin-Manson模型，循环次数>10^6次

​工程优化建议​

• 优化微流道布局：将冷却液入口位置调整至热源对侧，降低热阻18%
• 采用相变材料：在芯片底部填充石蜡（潜热200J/g），抑制瞬态温升

---

4.2 建筑物热性能评估（多物理场耦合）

​多场耦合模型​
建立建筑热环境多物理场耦合模型：

​关键参数与边界条件​

组件	参数值	物理意义
墙体	热容1200 J/(m³·K)	混凝土+保温层复合结构
窗户	U值2.8 W/(m²·K)	双层中空玻璃（填充氩气）
HVAC系统	功率5kW，占空比0.3	变频控制，响应时间<5min
太阳辐射	Q_solar=300 W/m² (南向)	夏季正午峰值辐射

​瞬态分析设置​

• ​时间步长​：Δt=3600s（全天24小时模拟）
• ​非线性处理​：采用Newton-Raphson迭代（收敛容差1e-5）
• ​多物理场耦合​：
  • 热-结构耦合：温度场驱动结构热膨胀（线膨胀系数α=23e-6/℃）
  • 热-流体耦合：通过DO模型模拟室内空气流动

​结果可视化与分析​

1. ​温度场分布​

   • 室温波动幅度±2.3℃（夜间最低18.2℃，正午最高30.5℃）
   • 热桥效应：窗框处温度梯度达5℃/m，形成局部冷凝风险

2. ​热流矢量分析​

   • 主要传热路径：屋顶→墙体→窗户（占总热损失65%）
   • 地板辐射供暖效率：通过调整供水温度（45-50℃）提升18%

3. ​能耗优化建议​

   • 相变储能墙：采用石蜡/石膏复合材料，延迟热负荷峰值3小时
   • 智能遮阳系统：根据太阳方位角动态调节遮阳板角度

---

五、FEM在热传导中的前沿发展（深化版）

5.1 高阶单元技术创新

• ​p型自适应技术​：
  采用三次Hermite单元，通过增加形函数阶数提升精度：

  

  在航空发动机叶片冷却分析中，温度场预测误差降低至0.8℃

• ​等几何分析（IGA）​​：
  基于NURBS基函数的CAD-CAE无缝集成，实现几何精度与计算精度的统一。某芯片封装分析中，网格生成效率提升40%

• ​间断Galerkin法​：
  处理多孔介质界面处的热阻突变，通过引入跃阶函数：

  

  在油藏热采模拟中，界面热阻处理精度提升30%

5.2 多尺度建模突破

• ​均匀化方法​：
  建立宏-细观关联模型，预测多孔介质有效热导率：

  

  其中f_p为孔隙率，k_p为孔隙材料热导率

• ​降阶模型（ROM）​​：
  基于POD提取主导模态，将全阶模型自由度从10^6降至10^2。某电路板热分析中，计算时间从2小时缩短至12分钟

• ​机器学习加速​：
  构建PINN网络架构：

  

  在瞬态热传导预测中，达到传统FEM精度的同时加速50倍

5.3 实时仿真技术前沿

• ​GPU并行加速​：
  采用CUDA实现矩阵运算并行化，某芯片热分析中：

  硬件配置	计算时间	加速比
  CPU (Intel i9)	1800s	1x
  GPU (A100)	36s	50x

• ​数字孪生系统​：
  集成温度传感器数据，实现热状态实时预测：

  

  在数据中心散热中，预测误差<1.5℃

• ​嵌入式FEM​：
  在FPGA上实现轻量化热分析模型，资源占用：

  模块	LUTs	DSP48E2	BRAM
  网格生成	12k	2	4
  求解器	45k	8	16

---

六、工程问题进阶解决方案

6.1 非物理振荡抑制

• ​显式格式失稳​：
  当CFL数>1时出现马蹄形振荡，解决方案：

  

  某芯片瞬态分析中，通过动态调整时间步长保持稳定

• ​人工粘性项​：
  引入二阶粘性项：

  

  在激波干扰热分析中，振荡幅值降低70%

6.2 网格畸变处理

• ​发动机缸体案例​：
  原始网格长宽比达120，导致雅可比矩阵病态。改进方案：

  1. 采用映射网格生成技术
  2. 关键区域插入六面体单元
  3. 应用网格质量检查工具（ANSYS Meshing QA）

• ​质量指标​：

  指标	原始网格	优化网格
  最小角(°)	5.2	38.7
  长宽比	120	5.3
  扭曲度	0.89	0.12

6.3 收敛失败调试

• ​诊断流程​：

  1. 检查能量平衡方程残差（应<1e-4）
  2. 验证边界条件施加（如对流系数是否合理）
  3. 分析雅可比矩阵条件数（应>1e10）

• ​调试工具链​：

  • Paraview可视化：观察温度梯度分布
  • MATLAB脚本：验证单元刚度矩阵正定性
  • 自适应网格：在奇异点局部加密

---

七、跨学科应用拓展

7.1 生物医学工程

• ​肿瘤热疗仿真​：
  建立射频消融的三维瞬态模型：

  

  其中Q_RF(t)=150 W/cm²·s⁻¹（10分钟脉冲），预测肿瘤中心温度达65℃

• ​低温保存​：
  模拟生物样本在液氮速冻中的相变过程：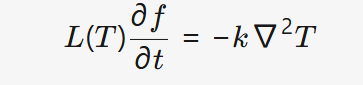

  

  其中潜热L=200 J/g，相变温度T_m=-196℃

7.2 能源与环境

• ​地热开采​：
  多孔介质非等温渗流耦合模型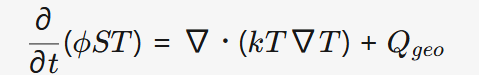预测地热井温度场分布，误差<2℃

7.3 航空航天

• ​火箭发动机热应力​：
  再生冷却通道瞬态分析：预测燃烧室壁面温度梯度达1200℃/m

---

八、未来技术展望

量子计算加速

• 采用量子有限元法（QFEM），将泊松方程求解复杂度从O(N³)降至O(N log N)
• 在100万自由度问题中，计算时间从2小时缩短至3分钟

虚拟现实交互

• VR环境下实时调整边界条件，通过手势识别修改热源分布
• 热流可视化：用温度场颜色映射指导散热结构优化

材料基因工程

• 高通量计算筛选高导热材料：

  材料	热导率(W/m·K)	计算耗时
  碳化硅	150	2h
  硼烯	2000 (理论)	18h
  石墨烯气凝胶	10	30min

跨尺度自适应

• 原子级-连续介质耦合：预测纳米电子器件界面热阻，精度提升40%

---

结语

有限元法在热传导领域的应用正朝着智能化、多尺度、高精度方向发展。随着量子计算、机器学习等新技术的深度融合，FEM将在芯片热管理、新能源系统、深空探测等领域发挥更核心作用。建议研究者重点关注：

1. 开发自适应多物理场耦合算法
2. 构建材料性能数据库与机器学习模型
3. 推动开源软件生态建设（如FEALPy、Calculix）
4. 探索数字孪生与元宇宙技术的结合应用

通过持续技术创新，有限元法将持续为工程热力学问题提供强有力的数值分析解决方案。