领导1v1谈话_让谈话强化学习基础知识1

最新推荐文章于 2024-11-05 15:32:33 发布

weixin_26704853

最新推荐文章于 2024-11-05 15:32:33 发布

阅读量928

点赞数

文章标签：强化学习 python

原文链接：https://medium.com/swlh/lets-talk-reinforcement-learning-the-fundamentals-part-1-65dcfcd7ed8a

版权

领导1v1谈话

Update: Part 2 is published! Let’s Talk Reinforcement Learning — The Fundamentals — Part 2

更新：第2部分已发布！ 让我们谈谈强化学习-基本原理-第2部分

Reinforcement Learning is a fascinating discipline. Q-learning being the most used state of the art RL algorithm, people often overlook the small ideas that piece together to form these algorithms. So in this article, I would like to concentrate more on the fundamental ideas that lay the foundation for RL.

强化学习是一门引人入胜的学科。 Q学习是最常用的RL算法，人们常常忽略了构成这些算法的小创意。因此，在本文中，我想将更多的精力集中在为RL奠定基础的基本思想上。

K-Bandit is a simple problem that can be used to understand the underlying basic blocks of reinforcement learning. So, let's dive into that

K-Bandit是一个简单的问题，可用于了解强化学习的基本基本知识。所以，让我们深入探讨

K-班迪问题 (The K-Bandit Problem)

Let us assume a scenario where we are developing a humanoid that treats sick patients. For simplicity, let’s narrow the sickness to a common cold. We give the humanoid three courses of treatment. Now it is up to the agent(humanoid — in RL literature, the term agent is widely used) to select the best of the three treatments. The catch here is we do not provide the efficacy of the treatments to the agent, but rather allow the agent to figure it in the due course of the time.

让我们假设一种情况，在这种情况下，我们正在开发一种可以治疗病人的类人动物。为简单起见，让我们将疾病范围缩小为普通感冒。我们给类人动物三个疗程。现在由药剂(类人动物，在RL文献中，术语“药剂”被广泛使用)选择三种治疗方法中的最佳方法。这里要注意的是，我们没有向代理商提供这种治疗的功效，而是让代理商在适当的时候对其进行计算。

The thing to notice here is that most machine learning and deep learning techniques are supervised or semi-supervised. But the K-Bandit problem requires the model to learn on the go right from the start.

这里要注意的是，大多数机器学习和深度学习技术都是受监督的或半监督的。但是，K-Bandit问题要求模型从一开始就可以随时进行学习。

Before Proceeding, take a minute to play this game and then come back. It will give you some intuition of what K-armed bandit problem really is.

在继续之前，请花一点时间玩此游戏，然后再回来。它会带给您一些真正的K武装匪徒问题的直觉。

Welcome back, I hope that the game was fun. So the three green boxes are the treatments available, the rewards are the efficacy and you were the agent. If you found out which box gave more rewards, congratulations you are a robot! Just kidding :-p

欢迎回来，我希望游戏很有趣。因此，三个绿色框是可用的治疗方法，回报是功效，而您是代理商。如果您发现哪个盒子提供了更多奖励，那么恭喜您是机器人！开玩笑的:-p

Okay… Now that you have a basic understanding of the problem, now what?

好吧...现在您已经对问题有了基本的了解，现在呢？

学什么？ (What to learn?)

The agent needs to know the value of action when the action is being taken. This can also be called as expected reward. If you know probability theory you may be familiar with the expectation of a random variable.

采取行动时，代理需要知道行动的价值。这也可以称为预期奖励。 如果您了解概率论，则可能熟悉随机变量的期望。

Reading the equation: q star of a is defined as the expectation of Rt, given we selected action A, for each possible action one through k. It will be summation for discrete values and integration for continuous values.

读等式：给定我们选择动作A到k的每个可能动作，将a的q星定义为Rt的期望。对于离散值将是求和，对于连续值将是求积分。

The goal is to maximize the reward. So let the argmax q* be the argument which maximizes the function q*(a). As q*(a) is unknown, we can estimate it. We can use Sample-Average Method to estimate the action value

目标是最大化奖励。因此，令argmax q *为使函数q *(a)最大化的参数。由于q *(a)未知，我们可以对其进行估计。我们可以使用“ 样本平均法”来估算作用值

I guess the formula is quite self-explanatory by itself. To understand it intuitively, let us consider a single action a. So Q_t(a) is the sum of all the rewards that have been recorded when action a has been taken divided by the total number of times the action a has been taken. There might be a question on why we use t-1 instead of t. It is because the expected reward is based on the actions taken before time t.

我猜想这个公式本身就很容易解释。为了直观地理解它，让我们考虑一个动作a 。所以Q_t(a)是所有当行动已经采取的总次数一个已采取的行动划分已记录的奖励的总和。关于为什么我们使用t-1而不是t可能存在一个问题。这是因为预期奖励是基于时间t之前采取的行动。

Getting our humanoid doctor here. The agent must decide which of the three possible treatments to prescribe. If the patient gets better, the agent records a reward of one. Otherwise, the agent records a reward of zero or punishment.

在这里找我们的人形医生。代理人必须决定要开三种可能的治疗方法中的哪一种。如果患者病情好转，代理会记录为1的奖励。否则，代理记录零或惩罚的奖励。

The agent prescribes the patient treatment-1 on the first time step and if the patient reports feeling better, the agent records a reward for the particular treatment and performs the process of estimation and updates the value. So this happens for multiple time steps. There will be a case where a patient reports no improvement in health to treatment-1. Now the agent can either record no reward or punish it by rewarding a negative value say -0.5.

代理在第一个时间步规定患者治疗-1，如果患者报告感觉好转，则代理会记录特定治疗的报酬并执行估算过程并更新值。因此，这发生在多个时间步骤上。在某些情况下，患者报告治疗1的健康不会改善。现在，代理可以不记录任何奖励，也可以通过奖励负值(例如-0.5)来惩罚它。

Do you see what is happening here? It’s just randomly picking a treatment and altering the treatment’s value after a patient reports back. If the agent continues this for many time steps, we will have in hand the data to estimate the true action values.

你看到这里发生了什么吗？在患者报告后，它只是随机选择一种疗法并更改其价值。如果代理在许多时间步骤中继续执行此操作，我们将掌握数据以估计真实的动作值。

Imagine what happens if doctors perform this kind of experiment in reality? Any sane doctor would not do this, rather he would choose the best treatment available. We call this method a greedy action selection. Instead of selecting the treatment at arbitrarily, we select the treatment that has the highest value. As straightforward as that, however, it doesn’t enable the agent to explore all the treatments instead we tend to exploit one treatment.

想象一下，如果医生在现实中进行这种实验会怎样？任何理智的医生都不会这样做，而是他会选择最佳的治疗方法。我们将此方法称为贪婪行动选择。 而不是任意选择治疗，我们选择具有最高价值的治疗。那样简单但是，它并不能使代理探索所有治疗方法，相反，我们倾向于采用一种治疗方法。

改变价值 (Changing Values)

We can estimate action values incrementally. To do this we can rewrite the sample average method as follows:

我们可以递增地估计动作值。为此，我们可以重写样本平均值方法，如下所示：

The error of the estimate is the difference between the old estimate and the new target. If we go towards the new target by one step, it will create a new estimate to reduce the error. Consider the stepsize like the learning rate in neural networks. So the stepsize can be a function n that produces a number 0 to 1. In our case the αₙ(stepsize) is 1/n. Now let’s go back to the humanoid doctor. Let’s say that treatment-2 performance is good during summer. Technically, it means that the distribution of the rewards changes with time. This is called a non-stationary bandit problem. So, do you see what αₙ is doing? It is just telling the agent to look past for a certain time-steps so that we get recent rewards and choose the appropriate action. If you know about time-series, you often see these cases in the form of trends & seasonalities.

估计的误差是旧估计与新目标之间的差。如果我们一步一步地达到新的目标，它将创建一个新的估计值以减少误差。考虑像神经网络中的学习率这样的步长。因此，步长可以是N的函数，其产生编号0到1。在我们的情况下，αₙ(步长)为1 / N。现在让我们回到类人动物医生那里。假设在夏季，治疗2的效果很好。 从技术上讲，这意味着奖励的分配会随着时间而变化。 这被称为非平稳土匪问题 。所以，你看到了什么αₙ是干什么的？这只是告诉代理人过去一定的时间，以便我们获得最近的奖励并选择适当的措施。如果您了解时间序列，通常会以趋势和季节性形式查看这些情况。

If you want to know the math behind this, I will provide the derivation and you can do your research on this.

如果您想了解其背后的数学原理，我将提供推导，您可以对此进行研究。

So now, what is the optimal stepsize? This brings us to the next part of the article exploration and exploitation.

那么，现在最佳的步长是多少？这将我们带到文章探索和开发的下一部分。

探索与开发权衡 (Exploration vs. Exploitation Tradeoff)

It is important to know whether the agent should explore or exploit. Exploring all the actions would give the agent a knowledge about the distribution of the actions which is surely beneficial for the long-term. But as you are now aware that exploiting would give results for the short-term but might fail in the longer run.

重要的是要知道代理是应该探索还是利用。探索所有动作将为代理提供有关动作分布的知识，这对于长期而言肯定是有益的。但是，正如您现在所知道的，利用将在短期内产生结果，但从长远来看可能会失败。

Exploitation — exploit knowledge for short-term benefit

剥削— 利用知识谋取短期利益

Exploration — improve knowledge for the long-term benefit

探索-为长远利益而提高知识水平

如何选择？ (How to choose?)

In the field of Machine Learning and Data Science, the bias-variance tradeoff is really a tricky one. But at the end of the day, the implementor would have experimented with various bias and variance settings and would have picked up a solution that he deems perfect for the particular problem. The same is the case with the exploration-exploitation tradeoff. Exploration leads to a more accurate estimation of our values and exploitation will yield you more rewards. However, we can do both at the same time.

在机器学习和数据科学领域，偏差方差的折衷确实是一个棘手的问题。但是最终，实现者将尝试各种偏差和方差设置，并且将获得他认为对特定问题最理想的解决方案。勘探与开发的权衡也是如此。探索可以更准确地估计我们的价值，而剥削将为您带来更多回报。但是，我们可以同时做这两个事情。

We can choose it randomly whether to exploit or explore. Choosing randomly is called Epsilon-Greedy. Say we roll a dice if it lands on 1 we explore else we exploit. Epsilon is the probability of exploring. So here, epsilon is 1/6 because the dice has 6 faces. In short, epsilon-greedy means pick the current best option (greedy) most of the time but pick a random option with a small (epsilon) probability sometimes.

我们可以随机选择是进行开发还是探索。随机选择称为Epsilon-Greedy 。假设我们掷骰子(如果它落在1上)，那么我们探索其他我们利用的骰子。 Epsilon是探索的可能性。所以在这里，ε是1/6，因为骰子有6个面。简而言之， epsilon- 贪婪意味着大多数时候都选择当前最佳选项(贪婪)，但有时选择概率很小(epsilon)的随机选项。

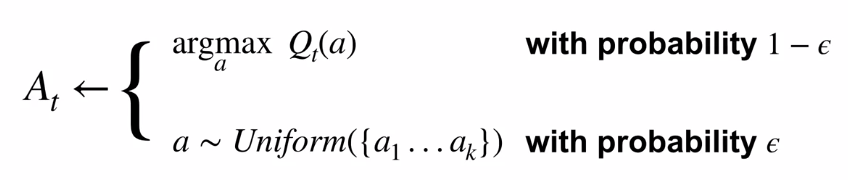
Another way is a decrementing approach. It suggests that start with an initial value assigned to all actions and overtime reduce the values until a particular action fails. This method is called Optimistic Initial Value.

另一种方法是递减方法。它建议从分配给所有操作的初始值开始，并超时减少这些值，直到特定操作失败为止。该方法称为乐观初始值 。

Another way to achieving the balance between exploration and exploitation is Upper-Confidence Bound(UCB) Action Selection.

实现勘探与开发之间的平衡的另一种方法是上置边界(UCB)动作选择。

Upper-Confidence Bound action selection uses uncertainty in the action-value estimates for balancing exploration and exploitation. Since there is inherent uncertainty in the accuracy of the action-value estimates when we use a sampled set of rewards thus UCB uses uncertainty in the estimates to drive exploration.

高置信度绑定动作选择使用动作值估计中的不确定性来平衡勘探和开发。由于当我们使用一组抽样的奖励时，行动价值估算的准确性存在内在的不确定性，因此UCB在估算中使用不确定性来推动勘探。

To Understand these methods in-depth, refer to Multi-armed Bandits

要深入了解这些方法，请参阅多臂匪

Also, play this game and observe how you are doing it. You might be able to think of the methods that are happening under the hood but it's implicit because you have a human brain!

另外，玩这个游戏，观察自己的表现。您也许可以想到幕后发生的方法，但这是隐含的，因为您有人脑！

外卖 (Takeaways)

i) In the k-armed bandit problem, we have an agent, who chooses between k different actions, and receives a reward based on the action he chooses.

i)在第k个武装匪徒问题中，我们有一个特工 ，他在k个不同的动作之间进行选择，并根据他选择的动作获得奖励。

ii) Fundamental ideas: actions, rewards, and value functions

ii) 基本思想 ：行动，奖励和价值功能

iii) Stepsize is the key for estimating action values

iii) 步长是估算行动价值的关键

iv) Exploration vs. Exploitation tradeoff

iv)探索与开发权衡

v) Methods to balance exploration and exploitation.

v)平衡勘探与开发的方法。

i) Reinforcement Learning — An Introduction 2nd edition [Richard S. Sutton and Andrew G. Barto]. Published by the MIT Press. This book is under the Creative Commons Attribution-NonCommercial-NoDerivs 2.0 Generic License. https://mitpress.ublish.com/ereader/2351/?preview#page/Cover

i)强化学习-入门第二版[Richard S. Sutton和Andrew G. Barto]。麻省理工学院出版社出版。本书受知识共享署名-非商业性-NoDerivs 2.0通用许可保护。 https://mitpress.ublish.com/ereader/2351/?preview#page/Cover

ii) The Epsilon-Greedy Algorithm[James D. McCaffery] https://jamesmccaffrey.wordpress.com/2017/11/30/the-epsilon-greedy-algorithm/

ii)Epsilon-Greedy算法[James D. McCaffery] https://jamesmccaffrey.wordpress.com/2017/11/30/the-epsilon-greedy-algorithm/

iii) Multi-armed Bandits a Naive form of Reinforcement Learning[Tamoghna Gosh] https://medium.com/@tamoghnaghosh_30691/multi-armed-bandits-a-naive-form-of-reinforcement-learning-a133c8ec19be

iii)多武装的土匪强化学习的一种朴素形式[Tamoghna Gosh] https://medium.com/@tamoghnaghosh_30691/multi-armed-bandits-a-naive-form-of-reinforcement-learning-a133c8ec19be