递归二进制搜索分析_二进制搜索树，我再次递归

递归二进制搜索分析

This week, I have been working on binary search trees, so this is an explanation of a problem that I did on Learn.co’s Software Engineering Post-Work track. It builds on the concept of Linked Lists, which I wrote about a couple of weeks ago. Just as a caveat, this is still something I am learning about and getting comfortable with!

本周，我一直在研究二进制搜索树，因此这是我在Learn.co的Software Engineering Post-Work轨道上遇到的一个问题的解释。 它建立在我几周前写的“链表”概念的基础上。 请注意，这仍然是我正在学习并逐渐感到满意的东西！

二进制搜索树示例 (Binary Search Tree Examples)

When using a binary search tree in JavaScript, numbers higher than the root go to the right of it, while numbers less than the root go to the left, as in the picture above. Below is a picture of another tree on the Flatiron School’s Learn.co.

在JavaScript中使用二进制搜索树时，高于根的数字位于其右侧，而小于根的数字则位于左侧，如上图所示。 下面是Flatiron学校的Learn.co上另一棵树的图片 。

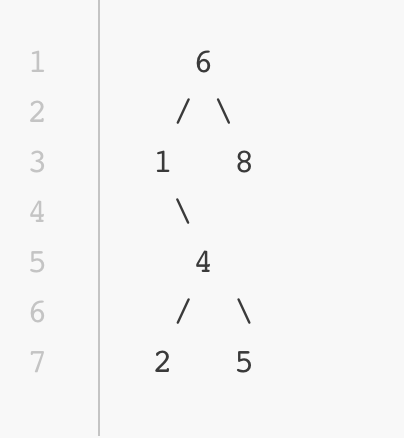
The pictures are just a heuristic. The code for the first tree pictured above looks like this, as we can see in the lab’s test file:

图片只是一种启发。 上图所示的第一棵树的代码如下所示，我们可以在实验室的测试文件中看到：

{data: 5, left:{data: 3, left: null, right: null},right: {data: 7, left: null,right: {data: 9, left: null, right: null}}}

Great — now let’s do a problem!

太好了-现在让我们做一个问题！

有一个While循环 (With a While Loop)

One of the parts of the lab I did asked me to write a function that takes in the root node and one other node; if the other node is found to be in the tree already, then the function returns ‘true.’ Otherwise, it adds the node in the appropriate place on the tree.

我做过实验的其中一部分，要求我编写一个接受根节点和另一个节点的函数。 如果发现另一个节点已经在树中，则该函数返回“ true”。 否则，它将节点添加到树上的适当位置。

The first approach I took to the problem uses a while loop. The recursive solution is in the works, so we’ll go with this one for now!

我对这个问题采取的第一种方法是使用while循环。 递归解决方案正在开发中，因此我们现在将继续使用它！

function findOrAdd (currentNode, newNode) {let quitLoop = 0;while(quitLoop < 1){if(currentNode.data === newNode.data){return true}else if(newNode.data < currentNode.data){if (!currentNode.left){currentNode.left = newNode;quitLoop = 1;}else{currentNode = currentNode.left;}}else {if (!currentNode.right) {currentNode.right = newNode;quitLoop = 1;}else {currentNode = currentNode.right;}}}return false;}

Before walking through the code, I’d like to direct your attention back to our friend the test file.

在遍历代码之前，我想将您的注意力吸引回我们的朋友测试文件。

查看测试文件 (Look at the Test File)

What is currentNode.data and newNode.data? If you look in the test file or comment out the rest of the code from the function and just return them, you can see what type of data the problem is expecting as inputs. Below is what we can learn from looking in the test file.

什么是currentNode.data和newNode.data？ 如果您查看测试文件或从函数中注释掉其余代码，然后仅返回它们，则可以看到问题将作为输入期望的数据类型。 以下是我们可以从查看测试文件中学到的知识。

let rootNode = {data: 5, left: null, right: null}let firstNewNode = {data: 3, left: null, right: null}let secondNewNode = {data: 7, left: null, right: null}let thirdNewNode = {data: 9, left: null, right: null}

The rootNode is what would be passed in as currentNode, or the head of the binary tree. The other three nodes are all examples of nodes that could be passed in as the second input. The test also shows us what it is expecting if the rootNode is entered as the first input and the firstNewNode is entered as the second input.

rootNode将作为currentNode或二叉树的头部传入。 其他三个节点都是可以作为第二个输入传递的节点的示例。 该测试还向我们显示了将rootNode输入为第一个输入并将firstNewNode输入为第二个输入时的期望。

findOrAdd(rootNode, firstNewNode)expect(rootNode.left).toEqual(firstNewNode)

The data for firstNewNode is 3, and since that is less than 5, it would go to the left. The test is actually pretty simple, since the left and right of the rootNode are both null. If the data of the second argument is larger, it goes to the right, and if it is smaller it goes to the left. Though my solution works with the current tests, I am not 100% sure that my solution would work the way that it is supposed to with a binary tree that has been built up more before using the function to add additional nodes. I did more testing myself — and though it seems to work, I have to think about it some more and get more practice.

firstNewNode的数据为3，由于该值小于5，因此它将转到左侧。 该测试实际上非常简单，因为rootNode的左侧和右侧均为null。 如果第二个自变量的数据较大，则它将移至右侧；如果较小，则它将向左侧。 尽管我的解决方案适用于当前的测试，但我不能100％地确定我的解决方案是否可以在使用该函数添加其他节点之前使用已经建立的更多的二叉树来实现。 我对自己进行了更多测试-尽管它似乎可以工作，但我仍需要多考虑一下并进行更多练习。

But for a first try with something new, let’s start small!

但是，首先尝试一些新事物，让我们从小处开始！

While循环的说明 (Explanation of the While Loop)

If currentNode.data is equal to newNode.data, then the function can return ‘true’ right away. Otherwise, if newNode.data is less than currentNode.data, if currentNode does not have a value to the left, the newNode can be inserted there. The variable quitLoop is set to 1 so the while loop will exit. However, if newNode.data is less than currentNode.data but there is already a value to the left of currentNode, then the currentNode variable is set to the value of currentNode.left and the while loop runs again until either a place on the tree is found for the newNode or it is discovered that the newNode is actually an old node already on the binary search tree — in which case the function will return true to signify that the tree already contains that node.

如果currentNode.data等于newNode.data，则该函数可以立即返回“ true”。 否则，如果newNode.data小于currentNode.data，则如果currentNode没有左侧的值，则可以在此处插入newNode。 变量quitLoop设置为1，因此while循环将退出。 但是，如果newNode.data小于currentNode.data但在currentNode的左侧已经有一个值，则将currentNode变量设置为currentNode.left的值，并且while循环将再次运行，直到树上的某个位置可以找到newNode或发现newNode实际上是已经在二进制搜索树上的旧节点-在这种情况下，该函数将返回true表示该树已经包含该节点。

If newNode.data is greater than currentNode.data, then the same process occurs, except it starts looking along the right side of what I am going to start imagining to be a Christmas tree. If the function makes it through the tree, finds a place for the newNode, and does not find data equal to the data in newNode, then it will return false and update the binary search tree to include the newNode in it.

如果newNode.data大于currentNode.data，则将发生相同的过程，除了它开始沿着我将要开始想象的圣诞树的右侧看。 如果该函数通过树，找到了newNode的位置，并且找不到与newNode中的数据相等的数据，则它将返回false并更新二进制搜索树以将newNode包含在其中。

So, that was my adventure with binary search trees. Don’t get lost in the branches, everyone!

因此，那是我使用二进制搜索树的冒险。 大家不要迷失在分支机构中！

演示地址

演示地址

翻译自: https://medium.com/@carlie.anglemire/binary-search-tree-and-me-recursion-again-again-c60814f868d8

递归二进制搜索分析