动态编程语言静态编程语言_您需要了解的有关动态编程的所有信息

最新推荐文章于 2021-12-11 16:00:36 发布

weixin_26746861

最新推荐文章于 2021-12-11 16:00:36 发布

阅读量474

点赞数

原文链接：https://medium.com/@codingtipsandlanguages/all-you-need-to-know-about-dynamic-programming-1242c299b330

版权

动态编程语言静态编程语言

什么是动态编程，为什么要关心它？ (What is dynamic programming and why should you care about it?)

In this article, I will introduce the concept of dynamic programming, developed by Richard Bellman in the 1950s, a powerful algorithm design technique to solve problems by breaking them down into smaller problems, storing their solutions, and combining these to get to the solution of the original problem.

在本文中，我将介绍由理查德·贝尔曼 ( Richard Bellman)在1950年代开发的动态编程概念，这是一种强大的算法设计技术，可以通过将问题分解为较小的问题，存储其解决方案并将其组合以得到解决方案，从而解决问题。原来的问题。

The hardest problems asked in FAANG coding interviews usually fall under this category. It is likely that you will get tasked with solving one during your interviews, hence the importance of knowing this technique. I will explain what dynamic programming is, give you a recipe to tackle dynamic programming problems, and will take you through a few examples so that you can understand better when and how to apply it.

FAANG编码面试中提出的最困难的问题通常属于此类。在面试过程中，您很可能需要解决一个问题，因此了解这一技术的重要性。我将解释什么是动态编程，为您提供解决动态编程问题的方法，并为您提供一些示例，以便您可以更好地了解何时以及如何应用它。

As I already did in my previous post about coding interviews, I will share my thought process when solving problems that can be solved using this methodology, so that you can do the same when you face one of them. I don’t want you to memorize anything. You need to understand the technique and practice to acquire the skill of turning ideas into code. Coding is not about learning programming languages. It is about analyzing a problem, considering different solutions, choosing the best one, and then implementing it in some programming language.

就像我在上一篇有关编程采访的帖子中已经做过的那样，我将分享我在解决使用这种方法可以解决的问题时的思考过程，以便面对其中的一个问题时也可以这样做。我不要你记住任何东西您需要了解技巧和实践，才能掌握将想法转化为代码的技巧。编码与学习编程语言无关。它是关于分析问题，考虑不同的解决方案，选择最佳解决方案，然后以某种编程语言来实现它。

动态编程 (Dynamic programming)

Dynamic programming is a general technique for solving optimization, search and counting problems that can be decomposed into subproblems. To apply dynamic programming, the problem must present the following two attributes:

动态编程是解决优化，搜索和计算可分解为子问题的问题的通用技术。要应用动态编程，该问题必须具有以下两个属性：

Optimal substructure.
最佳子结构。
Overlapping subproblems.
重叠的子问题。

最佳子结构 (Optimal substructure)

A problem has optimal substructure if the optimal solution to a problem of size n can be derived from the optimal solution of the same instance of that problem of size smaller than n.

如果可以从大小小于n的问题的同一实例的最优解中得出对大小为n的问题的最优解，则问题具有最优子结构。

For example, if the shortest path to go from Paris to Moscow goes through Berlin, it will be made of the shortest path from Paris to Berlin and the shortest path from Berlin to Moscow.

例如，如果从巴黎到莫斯科的最短路径经过柏林，它将由从巴黎到柏林的最短路径和从柏林到莫斯科的最短路径组成。

If a problem can be solved by combining optimal solutions to non-overlapping subproblems, the strategy is called divide and conquer. This is why merge sort and quick sort are not classified as dynamic programming problems.

如果可以通过将最优解决方案与非重叠子问题组合来解决问题，则该策略称为“ 分而治之” 。这就是为什么合并排序和快速排序未归类为动态编程问题的原因。

重叠子问题 (Overlapping subproblems)

Let’s take an example you’re probably familiar with, the Fibonacci numbers, where every number is the sum of the previous two Fibonacci numbers. The Fibonacci series can be expressed as:

让我们以您可能熟悉的斐波那契数为例，其中每个数字都是前两个斐波那契数之和。斐波那契数列可以表示为：

F(0) = F(1) = 1
F(n) = F(n-1) + F(n-2)

They say a picture is worth a thousand words, so here it is:

他们说一张图片值一千个字，所以这里是：

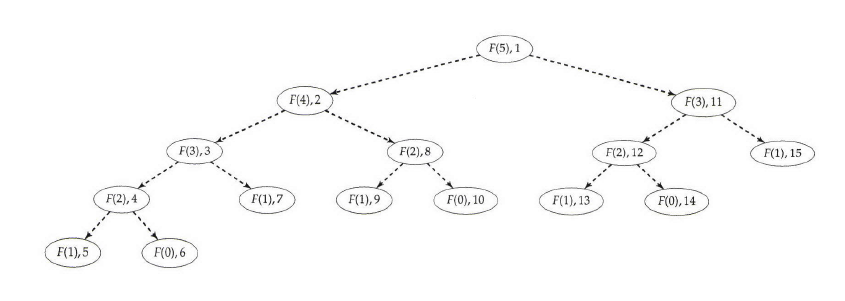
Image for post — From Elements of programming interviews

To solve F(n), you need to solve F(n-1) and F(n-2), but F(n-1) needs F(n-2) and F(n-3). F(n-2) is repeated, coming from two different instances of the same problem — computing a Fibonacci number.

要求解F(n)，需要求解F(n-1)和F(n-2)，但是F(n-1)需要F(n-2)和F(n-3)。重复F(n-2)，来自相同问题的两个不同实例-计算斐波那契数。

This can be expressed in a recursive function:

这可以用递归函数表示：

To solve a problem of size n, you call the same function to solve an instance of the same problem, but of a smaller size.
要解决大小为n的问题，您可以调用相同的函数来解决相同问题的实例，但是大小较小。
You keep calling the function until you hit a base case, in this example, n = 0 or n = 1.
您一直调用该函数，直到遇到基本情况为止，在本例中为n = 0或n = 1。

This leads us to the relationship between recursion and dynamic programming.

这使我们找到了递归和动态编程之间的关系。

递归和动态编程 (Recursion and dynamic programming)

Conceptually dynamic programming involves recursion. You want to solve your problem based on smaller instances of the same problem, and recursion is a natural way of expressing this in code. The difference with a pure recursive function is that we will trade space for time: we will store the optimal solution to the subproblems to be able to efficiently find the optimal solution to the problem that we originally wanted to solve.

从概念上讲，动态编程涉及递归。您希望基于相同问题的较小实例来解决问题，而递归是在代码中表达此问题的自然方法。纯递归函数的区别在于，我们将为时间交换空间：我们将为子问题存储最佳解决方案，以便能够有效地找到本来要解决的问题的最佳解决方案。

This is not to say that you must use recursion to solve dynamic programming problems. There is also an iterative way of coding a dynamic programming solution.

这并不是说您必须使用递归来解决动态编程问题。还有一种编码动态编程解决方案的迭代方法。

自下而上的动态编程 (Bottom-up dynamic programming)

You need to fill a table with the solution to all the subproblems (starting from the base cases) and use it to build the solution you are looking for. This is done in an iterative fashion, using one of the following:

您需要在表格中填写所有子问题的解决方案(从基本案例开始)，然后使用它来构建您要寻找的解决方案。使用以下方法之一以迭代方式完成此操作：

A multidimensional array (1D too) — the most commonly used.
多维数组(也是1D)—最常用。
A hash table.
哈希表。
A binary search tree.
二叉搜索树。

as your data structure to store the solutions to the subproblems.

作为您的数据结构来存储子问题的解决方案。

自顶向下的动态编程 (Top-down dynamic programming)

Code the recursive algorithm and add a cache layer to avoid repeating function calls.

编写递归算法的代码并添加一个缓存层，以避免重复调用函数。

This will all be much clearer when we start with the examples.

当我们从示例开始时，这将更加清楚。

如何解决动态编程问题 (How to attack a dynamic programming problem)

Optimal substructure and overlapping subproblems are the two attributes a problem must have to be solved used dynamic programming. You will need to verify this when your intuition tells you dynamic programming might be a viable solution.

最优子结构和重叠子问题是使用动态规划必须解决的两个属性。当您的直觉告诉您动态编程可能是可行的解决方案时，您将需要验证这一点。

Let’s try to get a feel for what kind of problems can be solved using dynamic programming. Things that start like:

让我们尝试使用动态编程可以解决什么样的问题。事情开始像：

Find the first n elements …
找到前n个元素...
Find all ways…
找到所有方式...
In how many ways …
以多种方式……
Find the n-th …
找到第n个……
Find the most optimal way…
寻找最佳方法...
Find the minimum/maximum/shortest path …
找到最小/最大/最短路径...

Are potential candidates.

是潜在的候选人 。

解决动态编程问题的步骤 (Steps to solve a dynamic programming problem)

Unfortunately, there is no universal recipe to solve a dynamic programming problem. You need to go through many problems until you start getting the hang of it. Do not get discouraged. This is hard. Maybe the hardest type of problems you will face in an interview. This is about modeling a problem with relatively simple tools — no need for fancy data structures or algorithms.

不幸的是，没有解决动态编程问题的通用方法。您需要经历许多问题，直到您开始掌握它。不要气disc。这很难。也许是您在面试中会遇到的最困难的问题。这是关于使用相对简单的工具为问题建模的方法-不需要花哨的数据结构或算法。

I have solved tons of them and still, sometimes I find it difficult to get to the solution. The more you practice, the easier it will be. This is the closest to a recipe to solve dynamic programming problems:

我已经解决了很多问题，但有时候，我发现很难找到解决方案。您练习得越多，就越容易。这是解决动态编程问题的最接近的方法：

Prove overlapping subproblems and suboptimal structure properties.
证明重叠的子问题和次优的结构特性。
Define subproblems.
定义子问题。
Define recursion.
定义递归。
Code your top-down or bottom-up dynamic programming solution.
对自上而下或自下而上的动态编程解决方案进行编码。

Complexity analysis varies from problem to problem, but in general, the time complexity can be expressed as:

复杂度分析因问题而异，但是通常，时间复杂度可以表示为：

Time ~ Number of subproblems * time per subproblem

时间〜子问题数*每个子问题的时间

It is straightforward to compute the space complexity for a bottom-up solution since it is equal to the space required to store solutions to the subproblems (multidimensional array).

计算自底向上解决方案的空间复杂度很简单，因为它等于将解决方案存储到子问题(多维数组)所需的空间。

例子 (Examples)

I’ve categorized some problems according to the number of independent dimensions involved. This is not necessary, but something that I have found it useful to have a mental model to follow when designing a solution. You will see patterns, as you code more and more. This is one of them (which I have not found explicitly described anywhere else). Use it if you find it helpful.

我已根据涉及的独立维度的数量对一些问题进行了分类。这不是必须的，但是我发现在设计解决方案时遵循一个心理模型很有用。随着编码的不断增加，您将看到模式。这就是其中之一(我在其他任何地方都没有明确描述)。如果发现有用，请使用它。

一维问题 (1D problems)

斐波那契 (Fibonacci)

Since by now you are very familiar with this problem, I am just going to present the recursive solution:

由于到目前为止您对这个问题非常熟悉，因此我将介绍递归解决方案：

int fib(int n) {
  if (n == 0 || n == 1)
    return 1;
  else
    return fib(n - 1) + fib(n - 2);
}

Going from recursive to top-down is usually mechanical:

从递归到自上而下通常是机械的：

Check if the value you need is already in the cache. If so, return it.
检查所需的值是否已在缓存中。如果是这样，请将其退回。
Otherwise, cache your solution before returning.
否则，请在返回之前缓存解决方案。

int fib(int n) {
  vector<int> cache(n + 1, -1);
  return fib_helper(n, cache);
}int fib_helper(int n, vector<int> &cache) {
   if(-1 != cache[n])
     return cache[n];   if (n == 0 || n == 1)
     cache[n] = 1;
  else
    cache[n] = fib_helper(n - 1, cache) + fib_helper(n - 2, cache);
  return cache[n];
}

And here, the bottom-up solution, where we build a table (from the base cases) to form the solution to the problem we’re looking for. This table is a 1D array: we only need to store the solution to a smaller version of the same problem to be able to derive the solution to the original problem.

这里是自下而上的解决方案，我们在此基础上构建了一个表(以基础案例为基础)，以解决我们正在寻找的问题。该表是一维数组：我们只需要将解决方案存储到相同问题的较小版本中，就可以得出原始问题的解决方案。

int fib(int n) { 
    vector<int> f(n + 1, 0);      f[1] = 1;     for(int i = 2; i <= n; i++) 
       f[i] = f[i - 1] + f[i - 2];     return f[n]; 
}

额外空间优化 (Extra space optimization)

This approach could be further optimized in memory, not time (there are faster techniques to compute Fibonacci numbers, but that is a topic for another article), by using just 3 variables instead of an array since we only need to keep track of 2 values, f(n-1) and f(n-2), to produce the output we want, f(n).

通过仅使用3个变量而不是数组，可以在内存中而不是时间上进一步优化此方法，而不是在时间上(有更快的技术来计算斐波那契数，但这是另一篇文章的主题)，因为我们只需要跟踪2个值即可，f(n-1)和f(n-2)产生我们想要的输出f(n)。

int fib(int n) {  
    if (n == 0 || n == 1) 
      return 1;    //Variables that represent f(n - 1), f(n - 2) and f(n)
    int n1= 1, n2 = 1, f = 0;     for (int i = 2; i <= n; i++) { 
        f= n1 + n2; 
        n2 = n1; 
        n1 = f; 
    }
    return f;
}

This is more advance, but a common pattern. If you only need to keep track of:

这是更先进的方法，但却是常见的模式。如果您只需要跟踪：

A few variables, you might be able to get rid of the 1D array and turn it into a few variables.
一些变量，您也许可以摆脱一维数组并将其转变为几个变量。
A few rows in a 2D matrix, you might be able to reduce it to a couple of 1D arrays.
在2D矩阵中的几行中，您可以将其简化为几个一维数组。
Etc.
等等。

Reducing dimensions we improve our space complexity. For now, you can forget about this, but after you get some practice, try to come up with these optimizations yourself to increase your ability to analyze problems and turn your ideas into code. In an interview, I would just go for the simpler version, just discussing potential optimizations and only implementing them if there is enough time after coding your “standard” dynamic programming solution.

减小尺寸可以改善空间复杂度。现在，您可以忘记这一点，但是在进行一些练习之后，请尝试自己进行这些优化，以增强分析问题的能力并将您的想法转化为代码。在一次采访中，我只是选择简单的版本，只讨论潜在的优化，只有在编码“标准”动态编程解决方案后有足够的时间才能实施这些优化。

爬楼梯 (Climbing stairs)

You are climbing a staircase. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

您正在爬楼梯。它需要n步才能到达顶部。每次您可以爬1或2步。您可以通过几种不同的方式登顶？

Example 1:

范例1：

Input: 2
输入2
Output: 2
输出2
Explanation: There are two ways to climb to the top: 1 step + 1 step and 2 steps
说明：有两种爬到顶部的方法：1步+ 1步和2步

Example 2:

范例2：

Input: 3
输入3
Output: 3
输出3
Explanation: There are three ways to climb to the top: 1 step + 1 step + 1 step, 1 step + 2 steps and 2 steps + 1 step
说明：有三种爬上顶部的方法：1步+ 1步+ 1步，1步+ 2步和2步+ 1步

解 (Solution)

Try to solve this problem on your own. You might be able to come up with a recursive solution. Go through my explanation and the previous examples to see if you can code a top-down solution.

尝试自行解决此问题。您也许可以提出一个递归解决方案。仔细阅读我的解释和前面的示例，看看是否可以编写自顶向下的解决方案。

A little hint: The fact that the question starts with “In how many ways”, should already make you think of a potential candidate for dynamic programming.

一个小提示：问题以“以多少种方式”开头，这一事实应该已经使您想到了动态编程的潜在候选人。

In this case, you want to reach step N. You can reach step number N from step N — 1 or N — 2 because you can jump 1 or 2 steps at a time. If you can solve these two subproblems, you can find the solution to the general problem. Let’s call f(N) the number of ways you can get to step N.

在这种情况下，您要到达步骤N。您可以从步骤N_1或N_2到达步骤号N，因为您一次可以跳1或2步。如果您可以解决这两个子问题，则可以找到一般问题的解决方案。让我们将f(N)称为获得步骤N的方法的数量。

To get f(N), you need f(N — 1) and f(N — 2).
要获得f(N)，您需要f(N_1)和f(N_2)。
To get to f(N — 1), you need f(N- 2) and f(N — 3).
要达到f(N_1)，您需要f(N-2)和f(N-3)。
For f(N — 2), you need f(N — 3) and f(N — 4).
对于f(N_2)，您需要f(N-3)和f(N-4)。

I don’t need to continue. You can already see that:

我不需要继续。您已经可以看到：

This problem has overlapping subproblems: you’ll need to compute multiple times f(N — 2), f(N — 3), f(N — 4), …
这个问题有重叠的子问题：您需要多次计算f(N_2)，f(N-3)，f(N-4)，...
This problem presents optimal substructure: with the optimal solution to f(N — 1) and f(N — 2), you can get the optimal solution to f(N).
这个问题代表了最优的子结构：通过对f(N_1)和f(N_2)的最优解，可以得到对f(N)的最优解。

which means dynamic programming can be used to solve it.

这意味着可以使用动态编程来解决它。

I will not write the code for this problem because … I have already done it in the previous example!

我不会编写此问题的代码，因为…在上一个示例中我已经完成了！

You can write and test your solution here.

您可以在此处编写和测试您的解决方案。

最长的增长子数组 (Longest increasing subarray)

Given an unsorted array of integers, find the length of the longest increasing subsequence. [10,9,2,5,3,7,101,18]

给定一个未排序的整数数组，请找出最长的递增子序列的长度。 [10,9,2,5,3,7,101,18]

The output would be 4, for the sequence [2,3,7,101]

对于序列[2,3,7,101]，输出将为4。

解 (Solution)

We need to find the length of the longest increasing subsequence for an array of size n. This sounds like an optimization problem, which could be a candidate for dynamic programming, so let’s try. Imagine that you already have the solution for a problem of size N — let’s call it s(n) — and you add an extra element to the array, called Y. Can you reuse part of the solution to X to solve this new problem? This mental experiment usually gives some good insight into the problem.

我们需要找到大小为n的数组的最长递增子序列的长度。这听起来像是一个优化问题，可能是动态编程的候选者，所以让我们尝试一下。想象一下，您已经有了解决大小为N的问题的解决方案(我们称它为s(n))，并且在数组中添加了一个名为Y的额外元素。您可以将解决方案的一部分重用于X来解决这个新问题吗？这个心理实验通常可以很好地洞察问题。

In this case, you need to know if the new element can extend one of the existing sequences:

在这种情况下，您需要知道新元素是否可以扩展现有序列之一：

Iterate through every element in the array, let’s call it X.
遍历数组中的每个元素，我们称之为X。
If the new element Y is greater than X, the sequence can be extended by one element.
如果新元素Y大于X，则可以将序列扩展一个元素。
If we have stored the solution to all the subproblems, getting the new length is trivial — just a lookup in an array. We can generate the solution to the new problem from the optimal solution to the subproblems.
如果我们已经将解决方案存储到所有子问题中，那么获得新的长度就很简单了-只需在数组中查找即可。我们可以从最佳解决方案到子问题生成新问题的解决方案。
Return the length of the new longest increasing subsequence.
返回新的最长递增子序列的长度。

We seem to have an algorithm. Let’s continue our analysis:

我们似乎有一个算法。让我们继续分析：

Optimal substructure: we’ve verified that the optimal solution to a problem of size n can be computed from the optimal solution to the subproblems.
最优子结构：我们已经验证了可以从子问题的最优解中计算出大小为n的问题的最优解。
Overlapping subproblems: To compute s(n), I’ll need s(0), s(1), …, s(n-1). In turn, for s(n-1), I’ll need s(0), s(1), …, s(n-2). The same problems needs to be computed multiple times.
子问题重叠：要计算s(n)，我需要s(0)，s(1)，…，s(n-1)。反过来，对于s(n-1)，我需要s(0)，s(1)，…，s(n-2)。相同的问题需要多次计算。

Here’s the code for the bottom-up solution.

这是自底向上解决方案的代码。

int lengthOfLIS(const vector<int>& nums) {
        if(nums.empty())
            return 0;        vector<int> dp(nums.size(), 1);
        int maxSol = 1;        for(int i = 0; i < nums.size(); ++i){
            for(int j = 0; j < i; ++j){
                if(nums[i] > nums[j]){
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            maxSol = max(maxSol, dp[i]);
        }
        return maxSol;   
}

You can write and test your solution here.

您可以在此处编写和测试您的解决方案。

多少个BST (How many BST)

Given n, how many structurally unique BSTs (binary search trees) that store values 1 … n?

给定n，多少个结构唯一的BST(二进制搜索树)存储值1…n？

Example:

例：

Input: 5
输入5
Output: 42
输出：42
Explanation: Given n = 5, there are a total of 42 unique BST’s
说明：给定n = 5，总共有42个唯一的BST

解 (Solution)

Let’s go through that example. Let’s imagine we have numbers the numbers 1,2,3,4,5. How can I define a BST?

让我们来看一个例子。假设我们有数字1,2,3,4,5。如何定义BST？

The only thing I really need to do is to pick one of the numbers as the root. Let’s say that element is number 3. I will have:

我唯一需要做的就是选择其中一个数字作为根。假设元素是3。我将拥有：

3 as root
3作为根
Numbers 1 and 2 to the left of 3.
3左边的数字1和2。
Numbers 4 and 5 to the right of 3.
3右边的数字4和5。

I can solve the same subproblem for (1,2) — let’s call this solution L — and (4,5) — let’s call this solution R — and count how many BST can be formed with 3 as its root, which is the product L * R. If we do this for every possible root and add all the results up, we have our solution, C(n). As you can see, being methodical and working from a few good examples helps design your algorithms.

我可以为(1,2)解决相同的子问题-我们将此解决方案称为L-和(4,5)-我们将该解决方案称为R-并计算以3为根可以形成多少BST，这就是乘积L *R。如果我们对每个可能的根都这样做，然后将所有结果相加，则得到解C(n)。如您所见，有条不紊地进行工作并从几个好的例子中学习有助于设计算法。

In fact, this is all that needs to be done:

实际上，这就是所有要做的事情：

Pick an element as the root of the BST.
选择一个元素作为BST的根。
Solve the same problem for numbers (1 to root — 1) and (root + 1 to n).
解决数字(1到根_1)和(根+1到n)的相同问题。
Multiply both the results for each subproblem.
将每个子问题的结果都相乘。
Add this to our running total.
将此添加到我们的运行总计中。
Move to the next root.
移至下一个根。

In fact, we don’t really care what numbers lie in each side of the array. We just need the size of the subtrees, i.e. the number of elements to the left and to the right of the root. Every instance of this problem will produce the same result. In our previous example, L is the solution to C(2) and so is R. We only need to compute C(2) once, cache it, and reuse it.

实际上，我们并不真正在意数组每一侧的数字。我们只需要子树的大小，即根的左侧和右侧的元素数。此问题的每个实例都会产生相同的结果。在我们之前的示例中，L是C(2)的解决方案，R是R.的解决方案。我们只需要计算一次C(2)，对其进行缓存并重新使用它。

int numTrees(int n) {
        vector<int> dp(n + 1, 0);        dp[0] = 1;
        dp[1] = 1;        for(int i = 2; i <= n; ++i){
            for(int j = 0; j < i; ++j){
                dp[i] += dp[j] * dp[i - 1 - j];
            }
        }
        return dp.back();
}

You can code and test your solution here.

您可以在此处编写代码并测试您的解决方案。

2D问题 (2D problems)

These problems are usually a little harder to model because they involve two dimensions. A common example is a problem where you have to iterate through two strings or to move through a map.

这些问题通常很难建模，因为它们涉及二维。一个常见的示例是一个问题，您必须遍历两个字符串或遍历地图。

The top-down solution is not much different: find the recursion and use a cache (in this case, your key will be based on 2 “indices”)
自上而下的解决方案没有太大区别：找到递归并使用缓存(在这种情况下，您的密钥将基于2个“索引”)
For the bottom-up, a 2D array will suffice to store the results. This might be reduced one or a couple of 1D arrays as I mentioned before, but don’t stress about this. I’m just mentioning it in case you see it when solving a problem. As I said in my other article, learning is iterative. First, focus on understanding the basics and add more and more details little by little.
对于自底向上，一个2D数组足以存储结果。正如我之前提到的，可以减少一个或几个一维数组，但是不要着急。我只是提到它，以防您在解决问题时看到它。正如我在另一篇文章中所说的那样，学习是迭代的。首先，着重于了解基础知识，并逐渐增加越来越多的细节。

最小路径总和 (Minimum path sum)

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

给定用非负数填充的amxn网格，请找到一条从左上到右下的路径，该路径将沿其路径的所有数字的总和最小化。

Note: You can only move either down or right at any point in time.

注意：您只能在任何时间点向下或向右移动 。

Example:

例：

Input: [ [1,3,1], [1,5,1], [4,2,1] ]
输入：[[1,3,1]，[1,5,1]，[4,2,1]]
Output: 7
输出：7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
说明：因为路径1→3→1→1→1使总和最小。

解 (Solution)

Minimizes should make you think of dynamic programming. Let’s analyze this further. We can get from any cell C with indices (i,j) (that is not on the top or left border) from cells A = (i-1, j) and B = (i,j-1). From this, we can see that some problems are going to be computed multiple times. Also, we if know the optimal solution to A and B, we can compute the optimal solution to the current cell as min(sol(A), sol(B)) + 1 — since we can only get to the current cell form A or B and we need one extra step to move from these cells to the current cell. In other words, this problem presents optimal substructure and overlapping problems. We can use dynamic programming.

最小化应该使您想到动态编程。让我们进一步分析。我们可以从A =(i-1，j)和B =(i，j-1)的任何具有索引(i，j)(不在顶部或左侧边界)的单元格C中获取。由此可见，一些问题将被多次计算。另外，如果我们知道A和B的最优解，我们可以将当前单元格的最优解计算为min(sol(A)，sol(B))+1-因为我们只能得到当前单元格的形式A或B，我们需要执行一个额外的步骤才能从这些单元格移至当前单元格。换句话说，此问题提出了最佳的子结构和重叠问题。我们可以使用动态编程。

Here’s the bottom-up solution.

这是自下而上的解决方案。

int minPathSum(const vector<vector<int>>& grid) {
        const int nrow = grid.size();        if(nrow == 0)
            return 0;        const int ncol = grid[0].size();        vector<vector<int>> minSum(nrow, vector<int>(ncol, 0));
        minSum[0][0] = grid[0][0];        for(int col = 1; col < ncol; ++col)
            minSum[0][col] = minSum[0][col - 1] + grid[0][col];        for(int row = 1; row < nrow; ++row)
            minSum[row][0] = minSum[row - 1][0] + grid[row][0];        for(int col = 1; col < ncol; ++col){
            for(int row = 1; row < nrow; ++row){
                minSum[row][col] = min(minSum[row - 1][col], minSum[row][col - 1]) + grid[row][col];
            }
        }
        return minSum[nrow - 1][ncol - 1];
}

The boundary conditions are defined over the border of the matrix. You can only get to the elements in the border in one way: moving one square to the right or down from the previous element.

边界条件在矩阵的边界上定义。您只能以一种方式到达边框中的元素：从上一个元素向右或向下移动一个正方形。

You can code and test your solution here.

您可以在此处编写代码并测试您的解决方案。

背包问题 (Knapsack problem)

Given two integer arrays val[0..n-1] and wt[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that the sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item or don’t pick it (0–1 property).

给定两个整数数组val [0..n-1]和wt [0..n-1]，分别表示与n个项目关联的值和权重。还要给定代表背包容量的整数W，找出val []的最大值子集，以使该子集的权重之和小于或等于W。您不能破坏任何项目，请选择完整的项目或不要选择它(0-1个属性)。

解 (Solution)

Try to come up with a recursive solution. From there, add a cache layer and you’ll have a top-down dynamic programming solution!

尝试提出一个递归解决方案。从那里，添加一个缓存层，您将获得一个自上而下的动态编程解决方案！

The main idea is that, for every item, we have two choices:

主要思想是，对于每个项目，我们有两种选择：

We can add the item to the bag (If it fits), increase our total value, and decrease the capacity of the bag.
我们可以将物品添加到袋子中(如果合适)，增加总价值，并减少袋子的容量。
We can skip that item, keep the same value, and the same capacity.
我们可以跳过该项目，保持相同的值和相同的容量。

After we’ve gone through every single combination, we just need to pick the max value. This is extremely slow, but it’s the first step towards a solution.

完成每种组合后，我们只需要选择最大值即可。这是非常缓慢的，但这是迈向解决方案的第一步。

Having to decide between two options (add an element to a set or skip it) is a very common pattern that you will see in many problems, so it’s worth knowing it and understanding when and how to apply it.

必须在两个选项之间做出决定(将元素添加到集合中或跳过它)是一种非常常见的模式，您会在许多问题中看到这种模式，因此值得了解它，并了解何时以及如何应用它。

// Recursive. Try to turn this into a piece of top-down DP code.
int knapSack(int W, int wt[], int val[], int n) { 
     if (n == 0 || W == 0) 
        return 0;     if (wt[n - 1] > W) 
        return knapSack(W, wt, val, n - 1); 
    else
        return max(val[n - 1] + knapSack(W - wt[n - 1],  wt, val, n - 1), knapSack(W, wt, val, n - 1)); 
}

A bottom-up solution is presented here:

这里提供了一个自底向上的解决方案：

// C style, in case you are not familiar with C++ vectors
int knapSack(int W, int wt[], int val[], int n) 
{ 
    int i, w; 
    int K[n + 1][W + 1];     for (i = 0; i <= n; i++) { 
        for (w = 0; w <= W; w++) { 
            if (i == 0 || w == 0) 
                K[i][w] = 0; 
            else if (wt[i - 1] <= w) 
                K[i][w] = max( val[i - 1] + K[i - 1][w - wt[i - 1]], K[i - 1][w]); 
            else
                K[i][w] = K[i - 1][w]; 
        } 
    } 
    return K[n][W]; 
}

最长公共子序列(LCS) (Longest common subsequence (LCS))

Given two strings text1 and text2, return the length of their longest common subsequence.

给定两个字符串text1和text2，返回它们最长的公共子序列的长度。

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, “ace” is a subsequence of “abcde” while “aec” is not). A common subsequence of two strings is a subsequence that is common to both strings.

字符串的子序列是从原始字符串生成的新字符串，其中删除了一些字符(可以是一个字符)，而不会更改其余字符的相对顺序。 (例如，“ ace”是“ abcde”的子序列，而“ aec”则不是)。两个字符串的共同子序列是两个字符串所共有的子序列。

If there is no common subsequence, return 0.

如果没有公共子序列，则返回0。

Example:

例：

Input: text1 = “abcde”, text2 = “ace”
输入：text1 =“ abcde”，text2 =“ ace”
Output: 3
输出3
Explanation: The longest common subsequence is “ace” and its length is 3.
说明：最长的公共子序列是“ ace”，其长度是3。

解 (Solution)

Again, compute the longest X makes me think that dynamic programming could help here.

再次，计算最长的X使我认为动态编程可以在这里有所帮助。

Since you already have some experience with dynamic programming, I’ll go straight to the 2 properties, from the example. Let’s call the strings A and B, and our solution to this problem f(A, B). The idea is to see whether the 2 last characters are equal:

由于您已经具有动态编程的经验，因此我将直接从示例中转到这两个属性。我们将字符串称为A和B，并将其称为f(A，B)。目的是查看最后两个字符是否相等：

If so, the LCS has at least length 1. We need to call f(A[0:n-1], B[0:n-1]) to find the LCS till that index, and add 1 because A[n] and B[n] are the same.
如果是这样，则LCS至少具有1的长度。我们需要调用f(A [0：n-1]，B [0：n-1])来找到直到该索引的LCS，并添加1，因为A [n ]和B [n]相同。
If not, we remove that last character from both strings -one at a time — and find which path produces the LCS. In other words, we take the maximum of f(A[0: n -1], B) and f(A, B[0:n-1])
如果不是，我们从两个字符串中删除最后一个字符(一次一个)，然后找出产生LCS的路径。换句话说，我们取f(A [0：n -1]，B)和f(A，B [0：n-1])的最大值
Overlapping subproblems: Let’s see what calls can we expect: (“abcde”, “ace”) produces x1 = (“abcd”, “ace”) and y1 = (“abcde”, “ac”); x1 will produce x12 = (“abc”, “ace”) and y12= (“abcd”, “ac”); y1 will produce (“abcd”, “ac”) and (“abcde”, “a”). As you can see, the problems same problems need to be computed multiple times.
子问题重叠：让我们看看可以期待什么调用：(“ abcde”，“ ace”)产生x1 =(“ abcd”，“ ace”)和y1 =(“ abcde”，“ ac”); x1将产生x12 =(“ abc”，“ ace”)和y12 =(“ abcd”，“ ac”)； y1将产生(“ abcd”，“ ac”)和(“ abcde”，“ a”)。如您所见，这些问题相同的问题需要多次计算。
Optimal substructure: Very similar to the longest increasing subsequence. If we add one extra character to one of the strings, A’, we can quickly compute the solution from all the cached results that we obtained from solving for A and B.
最佳子结构：与最长的子序列非常相似。如果我们在一个字符串A'中添加一个额外的字符，我们可以从对A和B求解得到的所有缓存结果中快速计算出结果。

Using examples to prove things is not the way you start a mathematical demonstration, but for a coding interview is more than enough.

用示例来证明事情不是您进行数学演示的方式，但是对于编码面试来说绰绰有余。

int longestCommonSubsequence(const string &text1, const string &text2) {
        const int n = text1.length();
        const int m = text2.length();        vector<vector<int>> dp(n + 1, vector<int>(m + 1,0));        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(text1[i-1] == text2[j-1]) 
                    dp[i][j] = dp[i-1][j-1]+1;
                else 
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[n][m];
}

You can code and test your solution here.

您可以在此处编写代码并测试您的解决方案。

结论 (Conclusion)

You need to become familiar with these problems because many others are just variations on these. But do not memorize them. Understand when and how to apply dynamic programming, and practice until you can easily turn your ideas into working code. As you have seen, it is about being methodical. You don’t need advanced knowledge of algorithms or data structures to solve the problems. Arrays are enough.

您需要熟悉这些问题，因为许多其他问题只是这些问题的变体。但是不要记住它们。了解何时以及如何应用动态编程，并进行实践，直到您可以轻松地将您的想法变成可行的代码。如您所见，这是有条不紊的。您不需要解决算法或数据结构方面的高级知识。数组就足够了。

I have not completed a time/space analysis. That is an exercise for you. Feel free to reach out with questions or comments.

我尚未完成时间/空间分析。这是您的一项练习。随时提出问题或意见。

I hope you found this useful. If so, like and share this article and follow me on Twitter.

希望您觉得这有用。如果是这样，请喜欢并分享此文章，并在Twitter上关注我。

翻译自: https://medium.com/@codingtipsandlanguages/all-you-need-to-know-about-dynamic-programming-1242c299b330

动态编程语言静态编程语言

weixin_26746861

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
动态编程语言静态编程语言_您需要了解的有关动态编程的所有信息

动态编程语言静态编程语言什么是动态编程，为什么要关心它？ (What is dynamic programming and why should you care about it?)In this article, I will introduce the concept of dynamic programming, developed by Richard Bellman in the ...
复制链接

扫一扫