将三角形绕点b顺时针旋转90度_【专题突破】图形旋转与翻折典型例题解析

来源：数学密码142857

本文主要介绍旋转与翻折的四大题型，旋转与等腰三角形、旋转与相似三角形、旋转与直角三角形、翻折与相似三角形，涉及到30°、一线三垂直、勾股大法、8字型、鸡爪型、半角模型、参数大法、分类讨论等等，并通过具体例题加以分析，文章行文框架如下：

正文如下，敬请赏析：

01

旋转与翻折

旋转与等腰三角形

先从最简单的题型说起，图形的旋转会产生等腰三角形，那么问题就会以这个以旋转中心为顶点的等腰三角形做文章。例如【2017徐汇区二模第18题】

如图，在△ABC中，∠ACB=α(90°＜α＜180°)，将△ABC绕着点A逆时针旋转2β(0°＜β＜90°)后得△AED，其中点E、D分别和点B、C对应，联结CD，如果CD⊥ED，请写出一个关于α与β的等量关系的式子________．  

下面用图示来看看这道题的解法吧

是不是秒懂啊？

再来一题【2015奉贤区二模第18题】

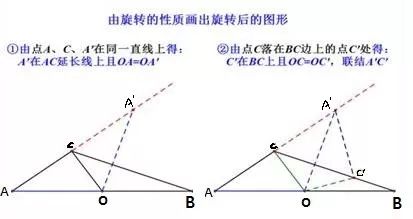
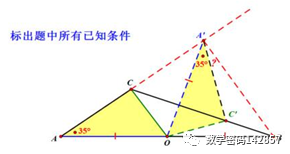
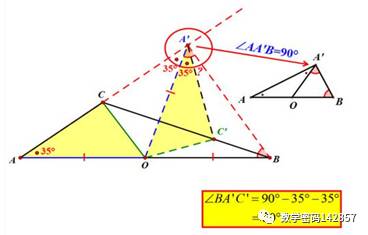
如图，已知钝角三角形ABC，∠A=35°，OC为边AB上的中线，将△AOC绕着点O顺时针旋转，点C落在BC边上的点C′处，点A落在点A′处，联结BA′，如果点A、C、A′在同一直线上，那么∠BA′C′的度数为________ 

继续用图示，看好啰

【2016崇明县第18题】

如图，在Rt△ABC中，∠ABC=90°，AB=BC