OpenCV 学习笔记03 boundingRect、minAreaRect、minEnclosingCircle、boxPoints、int0、circle、rectangle函数的用法...

函数中的代码是部分代码，详细代码在最后

1 cv2.boundingRect

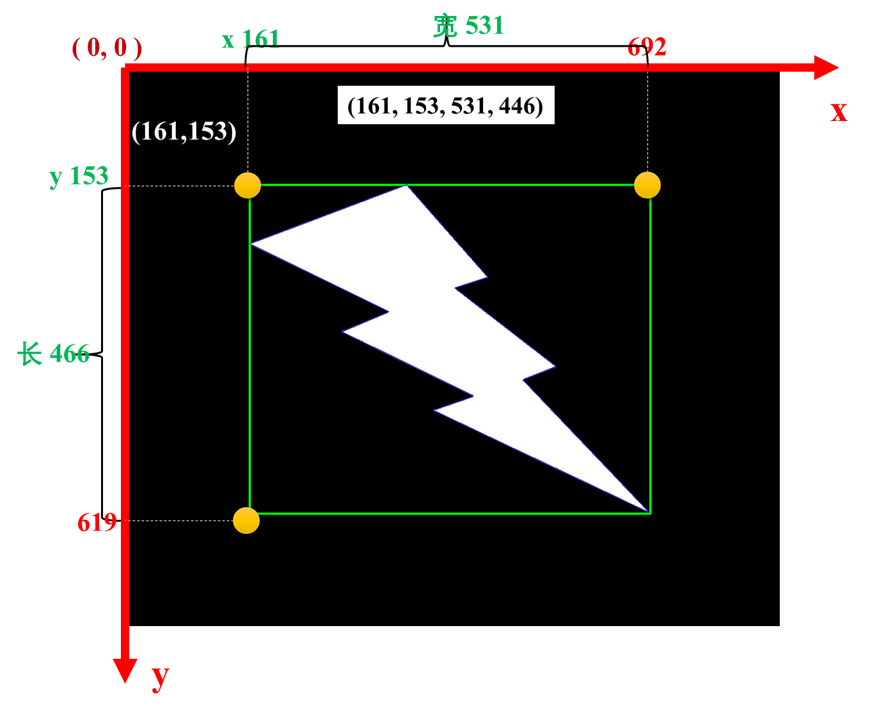
作用：矩形边框（boundingRect），用于计算图像一系列点的外部矩形边界。

cv2.boundingRect(array) -> retval

参数：

array - 灰度图像（gray-scale image）或 2D点集（ 2D point set ） 

返回值：元组

元组（x, y, w, h ) 矩形左上点坐标，w, h 是矩阵的宽、高，例如 (161, 153, 531, 446)

代码示例：

contours, hierarchy = cv2.findContours(re_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

for c in contours:
    # find bounding box coordinates
    # 现计算出一个简单的边界框
    x, y, w, h = cv2.boundingRect(c)
     # 画出矩形
    cv2.rectangle(img, (x,y), (x+w, y+h), (0, 255, 0), 2) 

 

 

2 cv2.minAreaRect

作用：minAreaRect - min Area Rect 最小区域矩形；计算指定点集的最小区域的边界矩形，矩形可能会发生旋转 possibly rotated，以保证区域面积最小。

cv2.minAreaRect(points) -> retval

参数：

points - 2D点的矢量（ vector of 2D points ）

返回值：元组

 元组（（最小外接矩形的中心坐标），（宽，高），旋转角度）----->    ((x, y), (w, h), θ )

关于旋转角度的注意事项：

1）旋转角度是水平轴（x轴）逆时针旋转，与碰到的矩形第一条边的夹角。

2）“ 第一条边 " 定义为 宽width，另一条边定义为高 height。这里的宽、高不是按照长短来定义的。

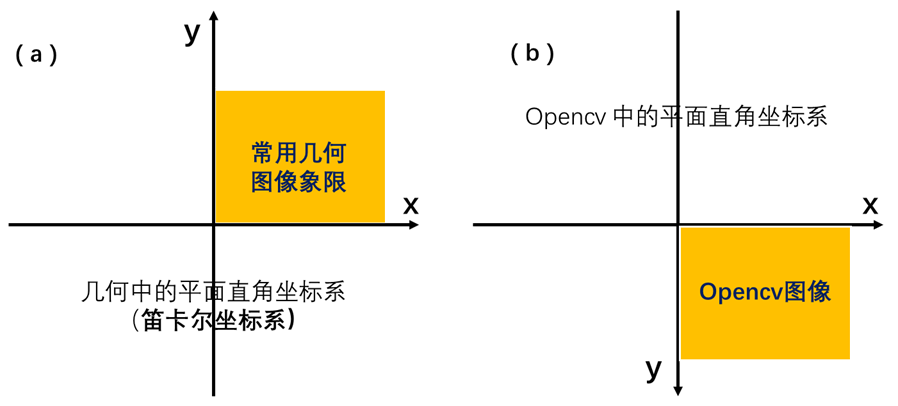
3）在 opencv 中，坐标系原点在图像左上角，将其延伸到整个二维空间，可以发现 “x轴镜像对称”，角度则 逆时针旋转为负、顺时针旋转为正。故θ∈（-90度，0]；（笛卡尔坐标系中，逆时针为正、顺时针为负）

4）旋转角度为角度值，而非弧度制。

 

 

如 ((458.70343017578125, 381.97894287109375), (202.513916015625, 634.2526245117188), -45.707313537597656)

但绘制这个矩形，一般需要知道矩形的 4 个顶点坐标；通常是通过函数 cv2.boxPoints()获取。

2.1 附1 : cv2.boxPoints

作用：查找旋转矩形的 4 个顶点（用于绘制旋转矩形的辅助函数）。

cv2.boxPoints(box) -> points

参数：

box - 旋转的矩形

返回值：列表list

points - 矩形 4 个顶点组成的列表 list

返回值示例：

[[614.9866  675.9137 ]
 [161.      232.99997]
 [302.4203   88.04419]
 [756.40686 530.9579 ]]

 

 

2.2 附2：int0

int0 有两种相近的描述，

第一种，int0 意味是 64位整数。字符代码'l'。与 Python int兼容，参考文档https://kite.com/python/docs/numpy.int0

int0 ( *args, **kwargs )

第二种，等价于intp，在 数组类型和类型之间的转换 文档中，有intp，释义为 “ 用于索引的整数（与C ssize_t