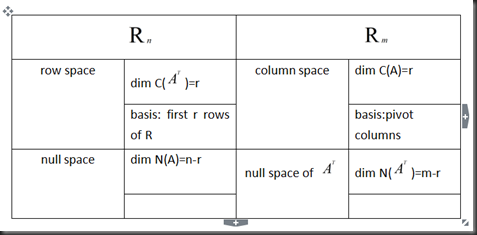
Four fundamental subspaces( for matrix A)
if A is m by n matrix:
Column space C(A) in Rm (列空间在m维实空间中)
Null space N(A) in Rn
Row space C(A^)(^代表转置)in Rn (all combinations of rows=all columns of A^)
Null space of A^ N(A^) in Rm (left null space of A 左零空间)
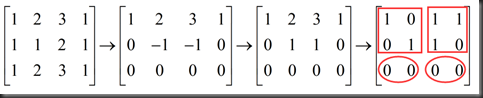
C(R) ≠ C(A)
different column space, same row space
“行变换不会对行空间产生影响,但“列空间”发生了变化
Basis for row space is first r rows of R
It’s called 基的最简形式
考虑:N(A^)
观察以上形式,所以称之为左零空间
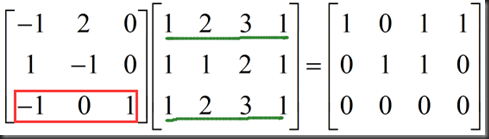
由Gauss-Jordan 方法可得:
我们在矩阵右侧增广矩阵,并进行相同的变换
let’s check
求矩阵的左零空间,试着找一个产生零行向量的行组合




 本文探讨了矩阵的四个基本子空间:列空间、零空间、行空间及左零空间的概念及其相互关系。通过行变换操作,我们了解到行空间保持不变而列空间可能会发生变化,并介绍了如何使用高斯-若尔当消元法来找到矩阵的左零空间。
本文探讨了矩阵的四个基本子空间:列空间、零空间、行空间及左零空间的概念及其相互关系。通过行变换操作,我们了解到行空间保持不变而列空间可能会发生变化,并介绍了如何使用高斯-若尔当消元法来找到矩阵的左零空间。

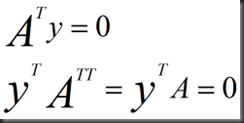
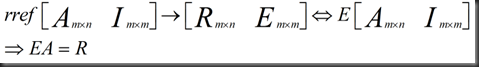

















 784
784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








