二维点集求外轮廓Java_从二维点集重建平面形状-浅议凹包算法

问题背景

近期遇到一个计算几何问题，需要从点集中重建一个合理的几何形状。这个问题既有二维的也有三维的，二维的情况相对简单一点，即给出平面区域的一系列散点，求出一定程度上反映这些散点轮廓的平面多边形，给出边的连接方式即可。如从下图的左图散点重建为右图的形状：

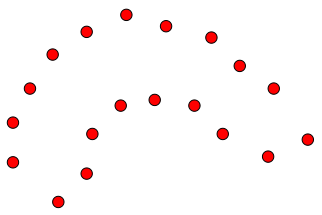
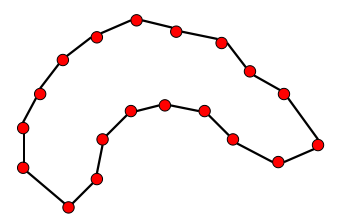
二维平面散点

平面多边形

不过这里有一些细节需要注意，必须明确这一系列点的含义，有时给出的点集是表征图形边界的，如左图的情况；有时则是表征图形所覆盖的范围，即在图形的内部也有一定的点分布。这两种不同的含义是和具体的应用场景相关的。

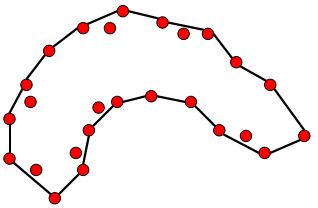
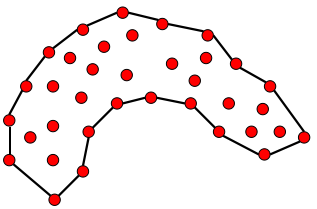
有的场景是求散点描绘的轮廓

有的场景是求散点分布区域的边界轮廓

凹包与Alpha shape

有不少计算几何领域的资料探讨过这一类问题的解决方案，笔者也曾经阅读过部分相关的文献，也在网络上进行过一些搜索。本文不能一一去介绍所有的方法，所以就介绍几种简单直观的方法来解决二维点集重建平面多边形的问题。

首先很多学计算机的人都知道凸包，凸包求取的是覆盖所有点的凸多边形，由于限定死了一定要凸多边形，所以凸包不是本文所讨论问题的解决方案。本文所求的形状肯定不能否定存在凹陷的部分，因而可以联想到这个问题的解是否是求一种“凹包”，或者说一种广义的参数化的凸包。事实上的确有凹包的概念，英文叫做concave hull(凸包叫convex hull)。不过于凸包的情况不同，凹包没有特别明确的定义，给定一个较不规则的点集，可以有各种各样的凹包，但凸包是确定的，如下图所示。

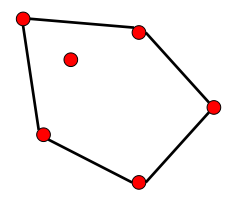
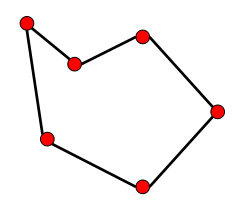
凸包

一种可能的凹包连接方式

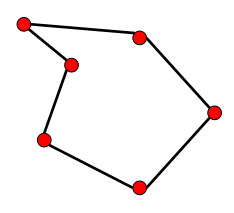
这样连也是凹包

进一步查找相关的资料可以发现一个叫做alpha shape的概念。这个概念最早出现于论文"On the shape of a set of points in the plane"中。alpha shape有较为正式的定义，若要简单点解释它，alpha shape其实就是在凸包基础上多了一个可以设定的参数α，因为这个α，在alpha shape重建形状的过程中可能就不会像凸包一样连接相距过远的顶点。参数α若趋于无穷大，则这个alpha shape会无无限接近凸包；而α取小了，则alpha shape会倾向于在一定位置凹陷进去，以更加贴合点集的外形。选择合理的α就能够控制生成的形状让其更加符合点集所描绘的形状。所以给出一个α值，就有点类似于给出一个长度的限制，例如让多边形的任何一边长度不超过R。

为了更好的展示和测试程序，笔者特地开发了一个基于WPF技术的小软件ConcaveGenerator用来展示算法效果，下文展示的很多图都是对这个软件截图的。如有兴趣可以在这里下载。

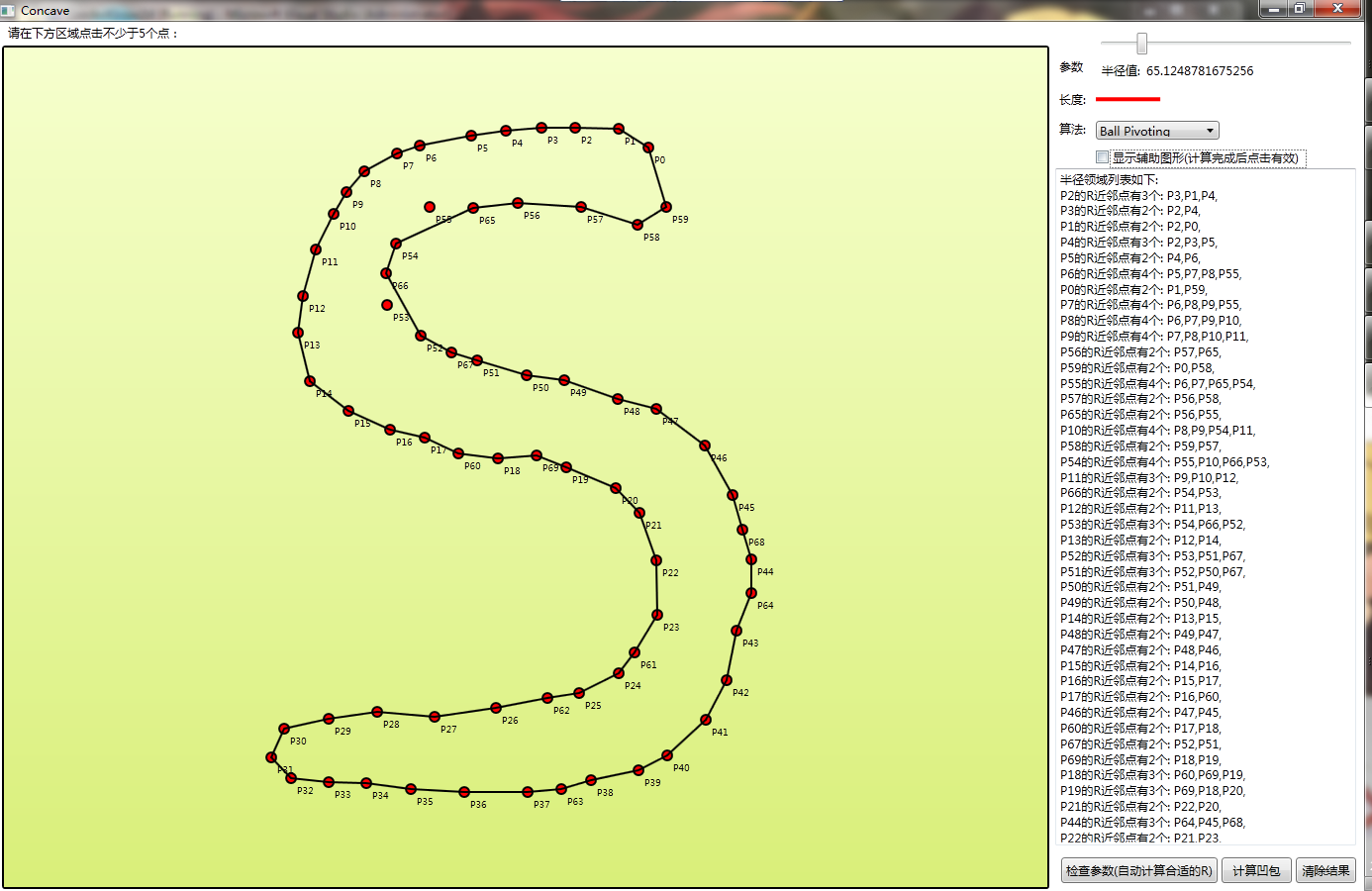
自制ConcaveGenerator小软件截图

第一种思路--基于Delaunay三角化

有一定计算几何基础的人一定熟悉Delaunay三角化，通过这一个过程可以形成Delaunay三角网，假如我们为想要求取形状的点集上使用Delaunay三角化算法，可以得到如下的三角网。

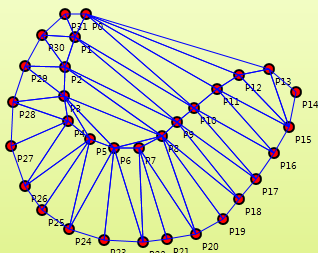
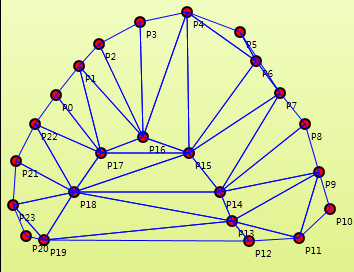
一个点集的Delaunay三角网

另一个例子

一看到这样的三角网，就不难想到一个好点子：因为我们想要求取的形状就是Delaunay三角网的子集，所以我们只需要从Delaunay三角网的最外层边开始外不断的删去超过长度限制的边，当这个过程结束时，我们就能够得到一个大致符合我们预期的形状。

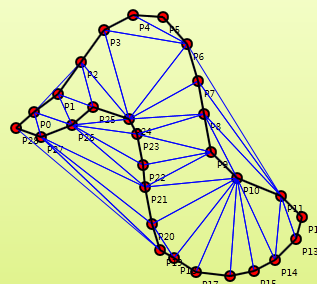
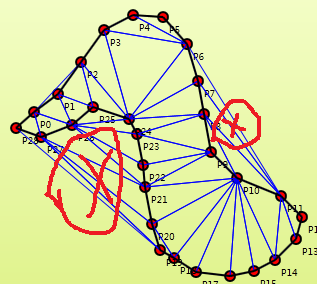
点集的Delaunay三角网

删掉边上太长的边就能形成预期的形状

所以总结这个思路，输入为点集S和长度限制R的求取凹包的边列表算法的过程如下：

为点集S求取Delaunay三角网M，三角网用标准Mesh形式表示。

为M初始化所有Edge对象，并求取Edge的长度以及邻接三角形集合。其中邻接2个三角形的边为内部边，1个三角形的为边界边，0个三角形的为计算过程中会退化的边。

将所有长度大于R的边界边加入队列，并当队列非空时循环下列过程：从队列中取出一条边E，得到E的唯一邻接三角形T。

找到T中另外两个边E1，E2将他们的邻接三角形集合删去T。

将E1,E2中新形成的长度大于R的边界边加入队列。

将E置无效标记，若E1,E2有退化的，也置无效标记。

收集所有有效的边界边，形成边列表，输出。

以下ConcaveGenerator是在这部分的代码，其中Delaunay三角化的实现有比较多的代码能参考，这里是使用了Stackoverflow上一个snippet：

public classDelaunayTriangulation

{public const int MaxVertices = 500;public const int MaxTriangles = 1000;public dVertex[] Vertex = newdVertex[MaxVertices];public dTriangle[] Triangle = newdTriangle[MaxTriangles];private bool InCircle(long xp, long yp, long x1, long y1, long x2, long y2, long x3, long y3, double xc, double yc, doubler)

{doubleeps;doublem1;doublem2;doublemx1;doublemx2;doublemy1;doublemy2;doubledx;doubledy;doublersqr;doubledrsqr;

eps= 0.000000001;if (Math.Abs(y1 - y2) < eps && Math.Abs(y2 - y3)

{return false;

}if (Math.Abs(y2 - y1)

{

m2= (-(Convert.ToDouble(x3) - Convert.ToDouble(x2)) / (Convert.ToDouble(y3) -Convert.ToDouble(y2)));

mx2= Convert.ToDouble((x2 + x3) / 2.0);

my2= Convert.ToDouble((y2 + y3) / 2.0);

xc= Convert.ToDouble((x2 + x1) / 2.0);

yc= Convert.ToDouble(m2 * (xc - mx2) +my2);

}else if (Math.Abs(y3 - y2)

{

m1= (-(Convert.ToDouble(x2) - Convert.ToDouble(x1)) / (Convert.ToDouble(y2) -Convert.ToDouble(y1)));

mx1= Convert.ToDouble((x1 + x2) / 2.0);

my1= Convert.ToDouble((y1 + y2) / 2.0);

xc= Convert.ToDouble((x3 + x2) / 2.0);

yc= Convert.ToDouble(m1 * (xc - mx1) +my1);

}else{

m1= (-(Convert.ToDouble(x2) - Convert.ToDouble(x1)) / (Convert.ToDouble(y2) -Convert.ToDouble(y1)));

m2= (-(Convert.ToDouble(x3) - Convert.ToDouble(x2)) / (Convert.ToDouble(y3) -Convert.ToDouble(y2)));

mx1= Convert.ToDouble((x1 + x2) / 2.0);

mx2= Convert.ToDouble((x2 + x3) / 2.0);

my1= Convert.ToDouble((y1 + y2) / 2.0);

my2= Convert.ToDouble((y2 + y3) / 2.0);

xc= Convert.ToDouble((m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 -m2));

yc= Convert.ToDouble(m1 * (xc - mx1) +my1);

}

dx= (Convert.ToDouble(x2) -Convert.ToDouble(xc));

dy= (Convert.ToDouble(y2) -Convert.ToDouble(yc));

rsqr= Convert.ToDouble(dx * dx + dy *dy);

r=