图像处理之模糊集合应用

supercolar

已于 2022-09-03 17:02:06 修改

阅读量2k

点赞数 2

分类专栏：数字图像处理文章标签：模糊集合图像处理

于 2019-10-14 09:12:37 首次发布

本文链接：https://blog.csdn.net/weixin_35732969/article/details/82835859

版权

数字图像处理专栏收录该内容

11 篇文章

订阅专栏

本文深入探讨了模糊逻辑在图像处理中的应用，介绍了模糊集合、隶属度函数的概念，以及如何通过模糊规则进行图像特征的识别与增强。文章还详细解释了模糊推理过程，包括输入颜色与成熟度的关系，以及如何通过去模糊化获得清晰的输出。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我的小程序：

举个例子：

假设我们要根据颜色将某水果分成3类：生的，半熟的和成熟的。假设经过观察得出如下结论：生的水果是绿色，半数的是黄色，成熟的是红色。标志绿黄红是颜色感觉的含混描述，要用模糊形式表达，可通过隶属度定义颜色（光的波长）的函数实现。输入的隶属度函数如下图：

上面提到的颜色和成熟度关系的知识可用下面的IF-THEN模糊规则给出：

IF-THEN规则中，THEN左侧部分称为前提（条件），右侧部分称为后果（结论）。

下一步，我们要寻找一种使用输入（颜色）和由IF-THEN规则描述的知识基础来创建模糊系统的输出方法。这一处理称为推断或推理。

我们处理的输出本身也是模糊的，必须定义输出的隶属度函数，如下图：

比较两幅图发现，输入输出的隶属度函数的自变量是不同的，一个是颜色，一个是成熟度。如果把两个隶属度函数以及基础规则结合起来看，结果将是二维的。例如”红色AND成熟“的表达，见下图：

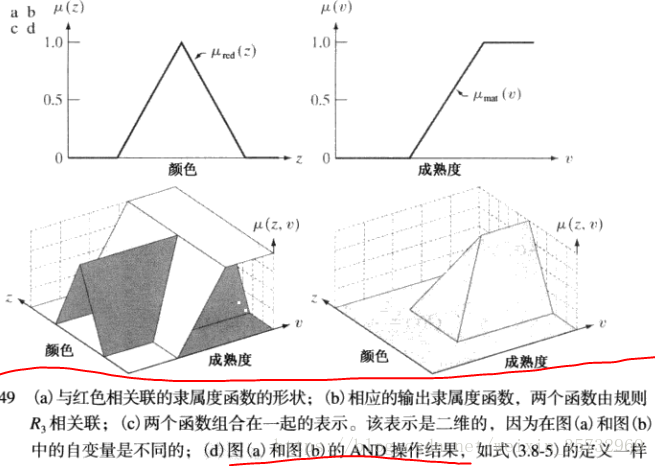
根据模糊集合的定义，AND定义为两个隶属度函数的最小，即：

$\mu _{3}(z,v) = min\{\mu_{red}(z),\mu_{mat}(v)\}$

下标3表示基础知识中规则 $R_{3}$ 的结果。上式是两个隶属度函数的通解，我们感兴趣的是特定输入的输出结果。令 $z_{0}$ 表示红色的一个特定值，则在 $\mu _{red}(z_{0})$ 和 $\mu _{3}(z,v)$ 间执行AND操作，并在 $z_{0}$ 处求值，可得到规则 $R_{3}$ 下的特定输入对应的输出：

$Q_{3}(v) = min\{\mu_{red}(z_{0}),\mu_{3}(z_{0},v)\}$

$Q_{3}(v)$ 表示规则3和一个特定输入导致的模糊输出。 $Q_{3}$ 中的唯一变量是所期望的输出变量v。

对于上式，分步来看。首先， $\mu_{red}(z_{0})$ 是一个常数，一个常数与 $\mu_{3}(z,v)$ 做最小操作，相当于截取掉 $\mu_{3}(z,v)$ 的顶部；其次，我们只对沿颜色轴的一个值 $z_{0}$ 感兴趣（即 $\mu_{3}(z_{0},v)$ ）,相当于沿着成熟轴截取一个剖面，该剖面位于 $z_{0}$ 处，见下图：

同理，可得到由其他两个规则和特定输入导致的模糊响应：

$Q_{2}(v) = min\{\mu_{yellow}(z_{0}),\mu_{2}(z_{0},v)\}$

$Q_{1}(v) = min\{\mu_{green}(z_{0}),\mu_{1}(z_{0},v)\}$

前面定义的3个规则是用OR连接的，所以，全部模糊输出如下：

$Q = Q_{1} \mathbf{OR} Q_{2} \mathbf{OR} Q_{3}$

OR写成最大操作的形式：

$Q(v) = \max_{r}\{\min_{s}\{\mu_{s}(z_{0}),\mu_{r}(z_{0},v)\}\}$

其中，r = {1,2,3}，s = {绿色，黄色，红色}。上式是通用的，可以将其扩展到n个规则，可令r = {1,2,3,...,n}；类似的可以把s扩展到包含任何有限数量的隶属度函数。

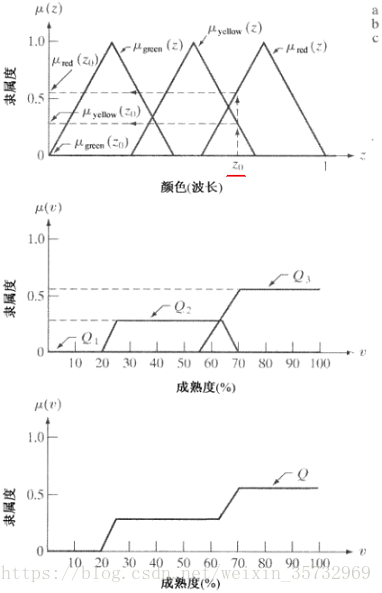
下图是对上面讨论的内容的一个总结。图(a)显示了在 $z_{0}$ 处计算的3个隶属度函数。图(b)显示了对输入 $z_{0}$ 的响应输出，这些模糊集合是上面图3.50(b)裁剪后的剖面，其中 $Q_{1}$ 由所有的0组成，因为 $\mu_{green}(z_{0})=0$ 。图(c)则是 $Q_{1},Q_{2},Q_{3}$ 的并集。

目前为止，我们得到了特定输入的完整输出，但它仍是个模糊集合。下一步称为去模糊：从模糊集合Q中得到”干脆的“输出 $v_{0}$ 。去模糊常用的方法是计算该集合的重心。如果Q(v)有K种可能的值Q(1),Q(2),...,Q(K)，则其重心为：

$v_{0} = \frac{\sum_{v=1}^{K}vQ(v)}{\sum_{v=1}^{K}Q(v)}$

从而得到一个”干脆的“输出。

下面，我们考虑规则中有多条件的情况，例如有一个规则：IF颜色是红色OR坚固性是软的，THEN水果是成熟的。此时除了定义颜色的隶属度函数，还需定义坚固性的隶属度函数。下图显示这种多条件的情况，并且把基于规则的模糊逻辑使用步骤总结如下：

补充：

当变量数很大时，常用方便的表示方法（变量，模糊集合）将一个变量和其对应的隶属度函数配对。例如，规则IF颜色是绿的，THEN水果是生的，在这里可以写成IF（z,绿色）THEN（v,生的），z和v表示颜色和成熟度，绿色和生的分别由隶属度函数 $\mu_{green}(z),\mu_{verd}(v)$ 定义的两个模糊集合。

当处理M个IF-THEN规则，N个输入变量 $z_{1},z_{2},...,z_{N}$ 和一个输出变量v，在图像中常用的规则公式如下:

$\begin{matrix} \mathbf{IF}(z_{1},A_{11})\mathbf{AND}(z_{2},A_{12})\mathbf{AND}...\mathbf{AND}(z_{N},A_{1N})\mathbf{THEN}(v,B_{1})\\ \mathbf{IF}(z_{1},A_{21})\mathbf{AND}(z_{2},A_{22})\mathbf{AND}...\mathbf{AND}(z_{N},A_{2N})\mathbf{THEN}(v,B_{2})\\ \mathbf{...}\\ \mathbf{IF}(z_{1},A_{M1})\mathbf{AND}(z_{2},A_{M2})\mathbf{AND}...\mathbf{AND}(z_{N},A_{MN})\mathbf{THEN}(v,B_{M})\\ \mathbf{ELSE}(v,B_{E}) \end{matrix}$