将长方形木框拉成平行四边形_我来探索平行四边形的面积

今天上课，我们开始新单元的学习，探索多边形的面积。

第一节课探索平行四边形的面积，如何把平行四边形转化成长方形是本节课教学的重要内容，掌握了这种转化的思想，也为学生探索三角形、梯形等面积的计算打下基础。

平行四边形是一节典型课，我听过许多专家讲这节课，其中贲友林老师对这节课的演绎，我听过三个不同版本，能感受到他一直在迭代。 虽然呈现方式不同，但大家对于这节课的关注点其实是一样的，平行四边形如何用剪拼法转化为长方形，拼成的长方形与原平行四边形有什么关系；而这节课的易错点就在于有的学生会用临边相乘求平行四边形的面积。

针对这几点，这节课我们设计了如下几个活动：

一、你能把平行四边形转化成长方形吗？(提示：可以画一画或者剪一个平行四边形操作演示)

针对这个活动孩子们有的画一画，也有的剪一剪，将平行四边形转化为长方形。在这个过程中，我们重点讨论了：1、剪的时候必须沿底边上的一条高剪，这样才能保证拼成的图形是长方形，否则拼成的图形还是平行四边形；2、孩子们起初都是剪下平行四边形的一角进行剪拼，那么还有其它的剪拼方法吗？孩子尝试发现，沿平行四边形的任意一条高减都可以。

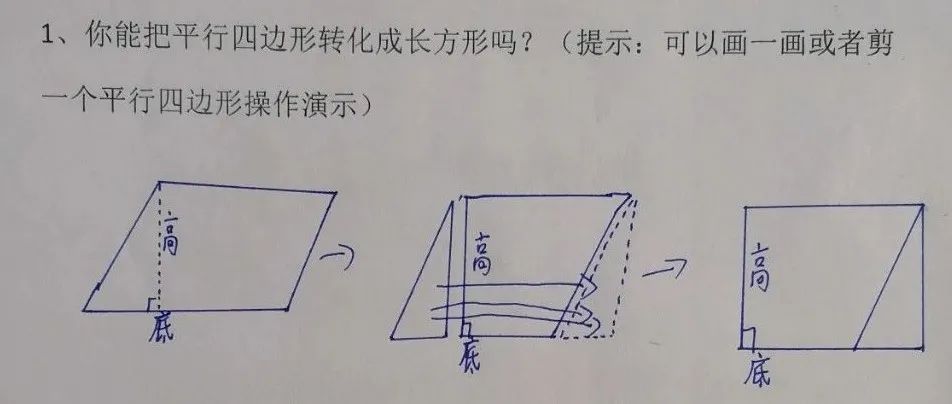
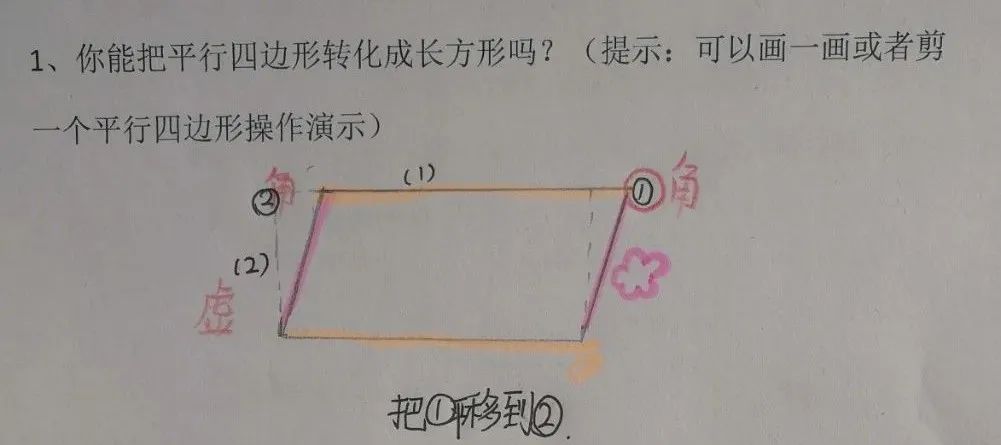
(如果不沿高剪，则拼成的图形还是平行四边形。)

二、转化成的长方形与原来的平行四边形的面积有什么关系？

这个问题比较好理解，因为剪拼的前后，只是形状发生改变，但是图形的大小不变，所以前后两个图形的面积不变。

三、怎样求平行四边形的面积？请结合图示进行说明。

对比转化前后的图形，发现平行四边形的高就是长方形的宽，平行四边形的底就是长方形的长，由长方形的面积等于长乘宽可以推导出平行四边形的面积等于底乘高。

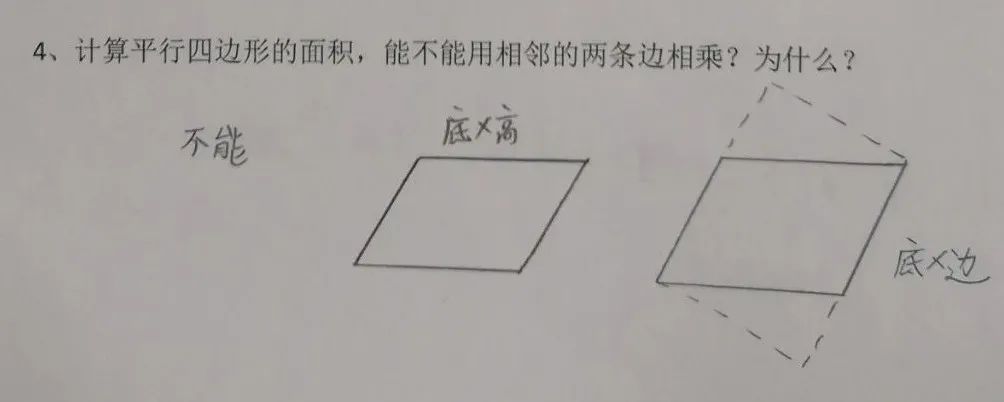
四、计算平行四边形的面积，能不能用相邻的两条边相乘？为什么？

这个问题是孩子们的痛点，特意拿出来大家讨论，通过操作学具对比，孩子发现：临边相乘所得长方形的面积比平行四边形的面积大。