向量场的散度和旋度_梯度、散度、旋度

梯度

如果我们把导数理解为微小变化引起的变化:

泰勒级数如下：

经常因为计算的原因我们可以利用线性的部分来做近似：

这也 make sense，相当于我们找到

处的切线，然后来看变化，毕竟这就是导数的本质定义。

这种思路对于具有多变量的函数应当也是适用的，比如空间中的曲面f(x,y):

对于这样的曲面，我们如果想要在

附近做线性的近似，那当然应该找到它对应的切平面。而切平面的方程为：

（切平面的方程可以通过找到x方向与y方向的切线，然后cross product得到法向量来证明。）

非常重要的是，上面这个式子同时也某种程度上回应了偏导数的本质，就是我们看x变量（方向）上的微小变化引起的变化，再加上y变量（方向）的微小变化引起的变化，就是总的变化。即使维度增加，线性模拟的式子应该也是类似的，比如函数 f(x,y,z) 在 (a,b,c) 处的线性近似应该是：

这也帮我们自然而然的引出了梯度（gradient）的概念：

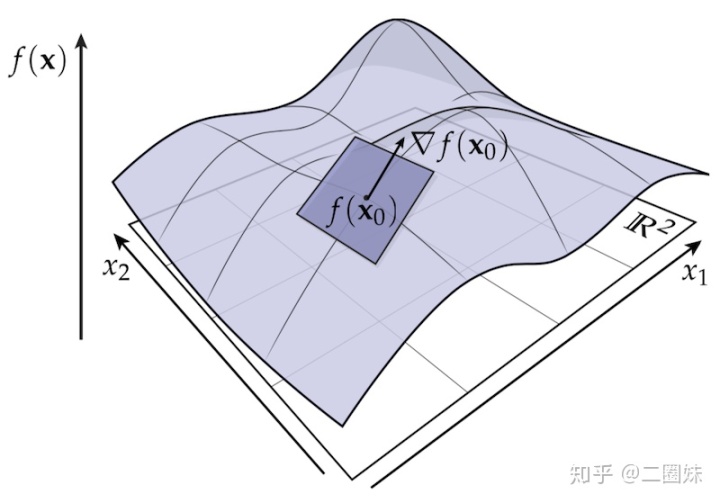
线性近似写成向量形式：

梯度就定义为：

Nabla算子：

以上式子也告诉我们，如果我们从

处动身：

• 沿着梯度方向走，函数值增大
• 沿着相反于梯度的方向走，函数值减小
• 垂直于梯度方向，函数值不变

同时这也呼应了许多算法，比如‘梯度下降法’，因为朝着相反梯度的方向，就是下降的最大的方向，同时因为以上我们指出的‘垂直于梯度方向，函数值不变‘，所以我们如果在等高线上看，我们总是朝着与等高线垂直的方向走：

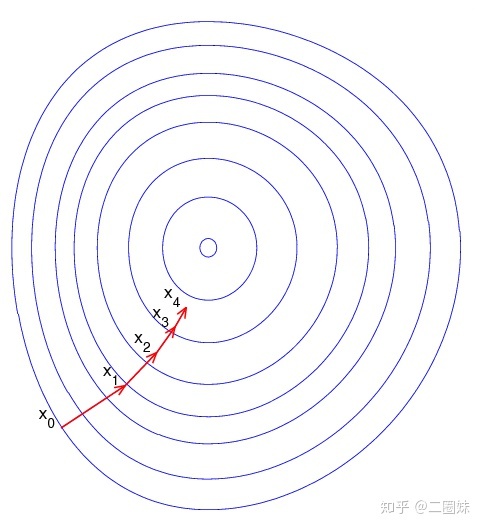
当然多元函数可以更多元，比如对于3d空间中的温度函数 f(x,y,z)，我们也可以求它的梯度，它的梯度我们计算出来就是一个三维空间中的向量场，这也是一个函数，如果我们代入空间中的每一点的数值，那么就可以知道其变化最快的方向和大小。当然也可以继续更多维度的函数

.

给我们一个多元函数，梯度的作用就是给了表示它变化的向量场。所以我觉得梯度跟导数更像一家人。

继续来看二次近似：

如果我们想把它推广到多元函数，那么我们会想应该也是类似的状况，除了前面的这一部分

， 我们会想要再加上二次的部分：

.

通过类比或者计算，我们都可以得到以上的二次近似的结果。

然后我们可以继续引出二次近似的向量形式：

其中 H 是 Hessian 矩阵：

当然我们也可以推广到更高的维度：

Hessian 矩阵必定是一个对称矩阵（比如之前的线性近似这是内积

, 按照内积的定义其实是看两个向量的对齐程度，这里我们某种程度上做的也是这件事，而在代表内积时，矩阵总是对称的，所以这里的矩阵也必定是对称的）。

来看一下关于内积的梯度：

如果这样来看：

所以这个结果就是：

其实跟就跟

差不多。

所以有一些对矩阵/向量求梯度的公式，都能找到对应的亲戚:

同时这也在呼应之前的说法‘梯度和导数更像一家人’。o(╯□╰)o

多元函数

带来了梯度，梯度的表现方式是向量场，这个场告诉我们的是空间中的每一个点这个多元函数变化的大小和方向。

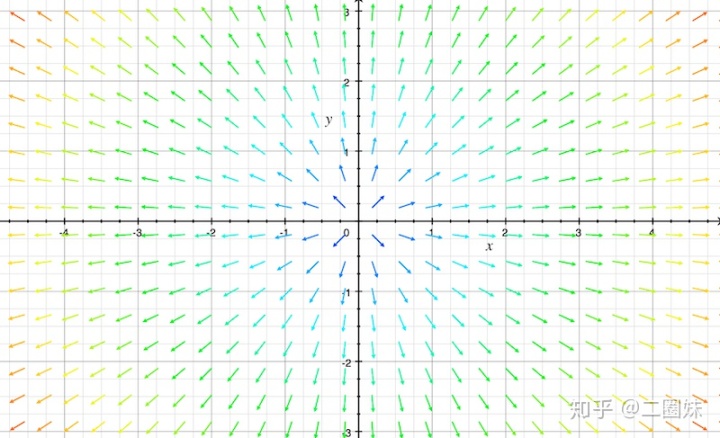
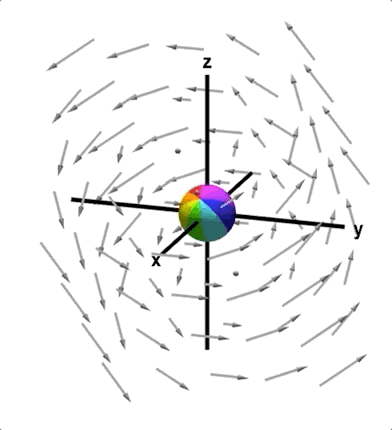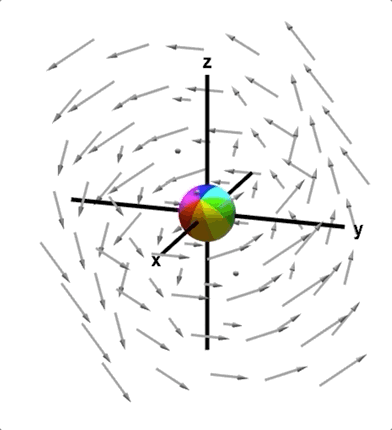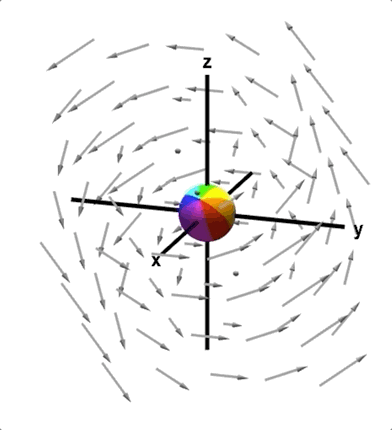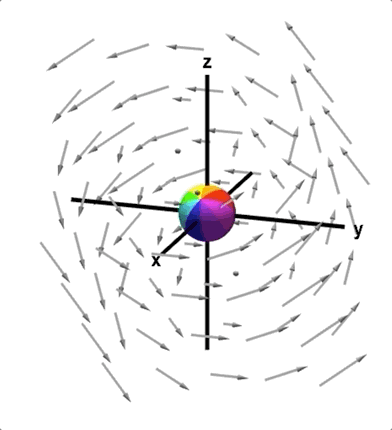
画向量场，一般用箭头表示它的指向，箭头长度表示它的大小，但是因为如果画出实际的大小可能会很乱，所以有些是用颜色来代表大小，越暖（红）就是此处的向量越大，越冷（蓝）就是越小。

向量场当然也是函数，因为对于空间中的每一点，都有一个对应的箭头，比如上图：

实际生活中有许多向量场：电场、磁场、重力场、速度场。

我喜欢将向量场想象为流动着的液体，这些液体在某一点的流速就是对应的箭头，这些液体当然不一定需要遵守物理规律，它们可以凭空出现或者消失，也可以随意的变换运动的方向。

那么这样会有两个相关的问题产生：

• 这些液体只是在空间中运动，空间中某点会流出液体么？（就像喷泉那样⛲️）或者这些液体会流入（像地上有个洞 ，液体会从这里流走）？
• 这些液体会在空间中旋转么？就像所谓的湍流或者龙卷风 那样？

这两个问题我们都可以通过分析向量场而知道，从而引出了散度和旋度的概念：

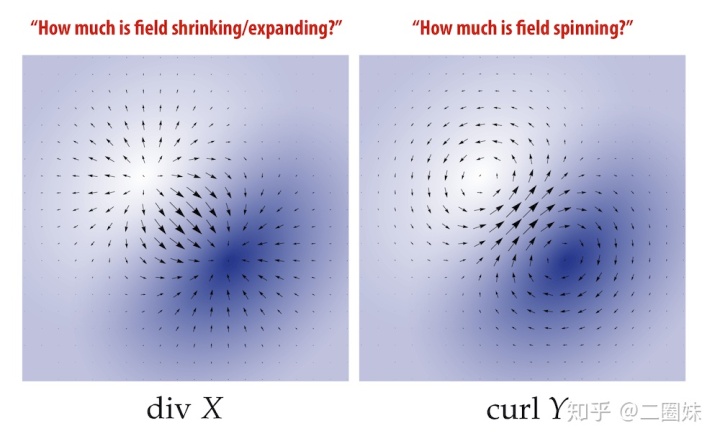
散度

像上面提到的，散度这个是用来表明空间中的这个点是否产生液体，其实也就是来看在此点处向内的箭头比较多还是向外的箭头比较多，我们现在来推导散度的表达式。

假设空间中有向量场

，那么观察空间中的微小的长方体：

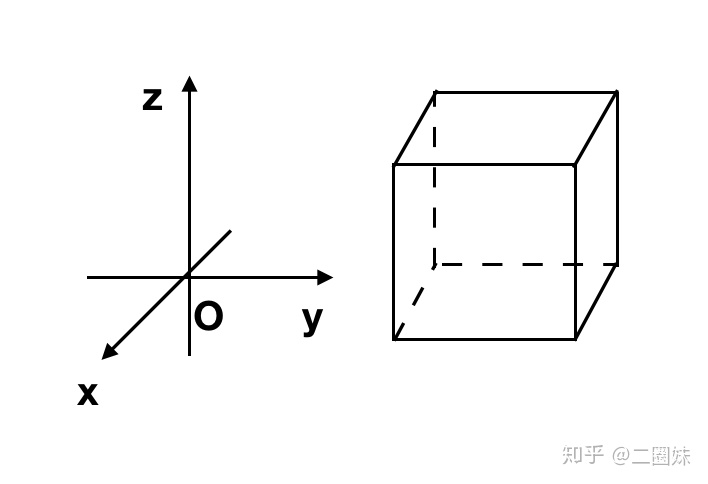
我们先就处理 x 轴方向的出入箭头之差,先看正面，如果这个长方体极小的话，我们可以做以下近似：

所以

这是针对长方体的，那么如果我们要长方体中的一点的话就是来看它的密度

：

同样，我们可以推导出 y 方向，z方向是也是类似的，这也就是我们的散度:

这就是这个点是否往外产生液体，散度我觉得是很好的翻译，而散度的英文 divergence 也有 ‘脱离,逸出’ 的意思，也是很表达它的意思了。

散度是给我们一个向量场，我们得到的是一个标量，代表的是一点是否有‘逸出’。

另外一个理解是既然我们想要知道的是三个方向的向量场的变化，我们当然就会想分别对它们求导，然后看最终的变化，这个散度我们也经常写成：

因为把

算子看做向量运算符，函数本身也是向量，所以是点乘的关系。

wikipedia 上关于散度的图会给我们更加直观的理解：

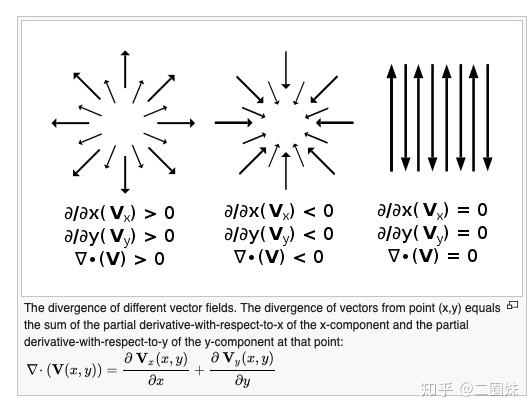
旋度

现在我们来解决第二个问题。考量与xy平面 平行的一个长方形：

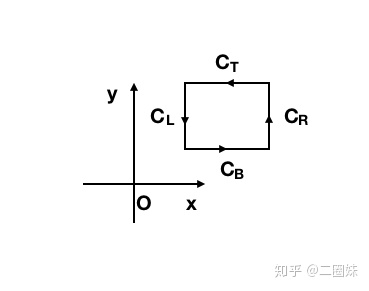
那么对于旋转的贡献：

除以面积，毕竟我们考察的是某点对于旋转的贡献：

同理我们看左边和右边：

所以有：

这是平行于xy平面的部分，同理我们可以继续求出平行于 xz 和 yz 的部分，最终会得到我们的旋度：

不是很容易记住，所以这个时候我们就可以感谢

算子了：

旋度是给我们一个向量场，我们得到的是一个向量，代表的是这一点的旋转情况。

参考：

• Vector Calculus