深度学习归一化方法[一] Batch Normalization

最新推荐文章于 2024-01-30 01:44:26 发布

Turtlelin007

最新推荐文章于 2024-01-30 01:44:26 发布

阅读量1.2k

点赞数 3

分类专栏： Deeplearning 文章标签： Batch Normalization 归一化

本文链接：https://blog.csdn.net/weixin_37142859/article/details/90320340

版权

Deeplearning 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

文章目录

- Batch Normalization

论文: https://arxiv.org/pdf/1502.03167.pdf

Batch Normalization

对模型的初始输入进行归一化处理，可以提高模型训练收敛的速度;对神经网络内层的数据进行归一化处理，同样也可以达到加速训练的效果。Batch Normalization 就是归一化的一个重要方法。以下将介绍BN是如何归一化数据，能起到什么样的效果以及产生该效果的原因展开介绍。

1. Batch Normalization原理

(一)前向传播

在训练阶段：
(1)对于输入的mini-batch数据 $\mathcal{B}=\left\{x_{1 \ldots m}\right\}$ ，假设shape为(m, C, H, W),计算其在Channel维度上的均值和方差：
$\begin{aligned} \mu_{\mathcal{B}} &= \frac{1}{m} \sum_{i=1}^{m} x_{i}\\ \sigma_{\mathcal{B}}^{2} &= \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} \end{aligned}$
(2)根据计算出来的均值和方差，归一化mini-Batch中每一个样本：
$\widehat{x}_{i} = \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}$
(3)最后，对归一化后的数据进行一次平移+缩放变换：
$y_{i} = \gamma \widehat{x}_{i}+\beta \equiv \mathrm{B} \mathrm{N}_{\gamma, \beta}\left(x_{i}\right)$
$\gamma、\beta$ 是需要学习的参数。

在测试阶段：
使用训练集中数据的 $\mu_{\mathcal{B}}$ 和 $\sigma_{\mathcal{B}}^{2}$ 无偏估计作为测试数据归一化变换的均值和方差：
$\begin{array}{l}{E(x)=E_{\mathcal{B}}\left(\mu_{\mathcal{B}}\right)} \\ {\operatorname{Var}(x)=\frac{m}{m-1} E_{\mathcal{B}}\left(\sigma_{\mathcal{B}}^{2}\right)}\end{array}$
通过记录训练时每一个mini-batch的均值和方差最后取均值得到。
而在实际运用中，常动态均值和动态方差，通过一个动量参数维护:
$\begin{aligned} r \mu_{B_t} &=\beta r \mu_{B_{t-1}}+(1-\beta) \mu_{\mathcal{B}} \\ r \sigma_{B_t}^{2} &=\beta r \sigma_{B_{t-1}}^{2}+(1-\beta) \sigma_{\mathcal{B}}^{2} \end{aligned}$
$\beta$ 一般取0.9.
因此可以得到测试阶段的变换为：
$\gamma \frac{x-E(x)}{\sqrt{Var(x)+\epsilon}} + \beta$
或：
$\gamma \frac{x-r \mu_{B_t}}{\sqrt{r \sigma_{B_{t-1}}^{2}+\epsilon}} + \beta$

（二）反向传播（梯度计算）
计算梯度最好的方法是根据前向传播的推导公式，构造出计算图，直观反映变量间的依赖关系。
前向传播公式：
$\begin{aligned} \mu_{\mathcal{B}} &= \frac{1}{m} \sum_{i=1}^{m} x_{i}\\ \sigma_{\mathcal{B}}^{2} &= \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}\\ \widehat{x}_{i} &= \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}\\ y_{i} &= \gamma \widehat{x}_{i}+\beta \end{aligned}$
计算图：

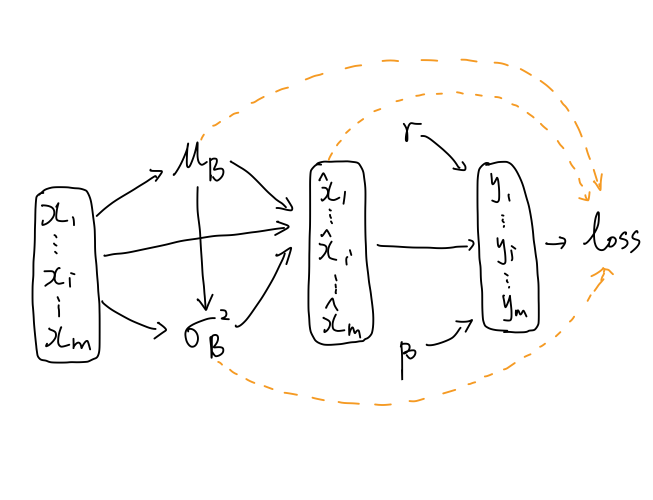
黑色线表示前向传播的关系，橙色线表示反向传播的关系
利用计算图计算梯度的套路：

先计算离已知梯度近的变量的梯度，这样在计算远一点变量的梯度时，可能可以直接利用已经计算好的梯度；
一个变量有几个出边（向外延伸的边），其梯度就由几项相加。

当前已知 $\frac{\partial l}{\partial y_{i}}$ ,要计算loss对图中每一个变量的梯度.
按照由近及远的方法,依次算 $\gamma,\beta,\hat{x_i}$ .由于 $\sigma_{\mathcal{B}}^2$ 依赖于 $\mu_{\mathcal{B}}$ ,所以先计算 $\sigma_{\mathcal{B}}^2$ ,再计算 $\mu_{\mathcal{B}}$ ,最后计算$x_i
$
$\gamma$ :表面一个出边,实际上有m个出边,因为每一个 $y_i$ 的计算都与 $\gamma$ 有关,因此
$\begin{aligned} \frac{\partial l}{\partial \gamma} &= \sum_{i=1}^m \frac{\partial l}{\partial y_i}\frac{\partial y_i}{\partial \gamma}\\ &= \sum_{i=1}^m \frac{\partial l}{\partial y_i} \hat{x_i} \end{aligned}$
$\beta$ :同理
$\begin{aligned} \frac{\partial l}{\partial \beta} &= \sum_{i=1}^m \frac{\partial l}{\partial y_i} \frac{\partial y_i}{\partial \beta}\\ &= \sum_{i=1}^m \frac{\partial l}{\partial y_i} \end{aligned}$
$\hat{x_i}$ :一条出边
$\begin{aligned} \frac{\partial l}{\partial \hat{x_i}} & =\frac{\partial l}{\partial y_i}\frac{\partial y_i}{\partial \hat{x_i}}\\ & =\frac{\partial l}{\partial y_i}\gamma \end{aligned}$
$\sigma_{\mathcal{B}}^2$ :m条出边,每一个 $\hat{x_i}$ 的计算都依赖于 $\sigma_{\mathcal{B}}^2$ .找到其到loss的路径: $\sigma_{\mathcal{B}}^2\rightarrow\hat{x_i}\rightarrow y_i \rightarrow loss$ ,由于 $\hat{x_i}$ 关于loss的梯度已经计算好了,所以路径为 $\sigma_{\mathcal{B}}^2\rightarrow\hat{x_i} \rightarrow loss$ ,因此
$\begin{aligned} \frac{\partial l}{\partial \sigma_{\mathcal{B}}^2} &= \sum_{i=1}^m \frac{\partial l}{\partial \hat{x_i}}\frac{\hat{x_i}}{\sigma_{\mathcal{B}}^2}\\ &= \sum_{i=1}^m \frac{\partial l}{\partial \hat{x_i}} \frac{-1}{2}(x_i-\mu_{\mathcal{B}})(\sigma_{\mathcal{B}}^2+\epsilon)^{-\frac{3}{2}} \end{aligned}$
$\mu_{\mathcal{B}}$ 出边有m + 1条.路径: $\mu_{\mathcal{B}} \rightarrow \sigma_{\mathcal{B}}^2 \rightarrow loss$ , $\mu_{\mathcal{B}} \rightarrow \hat{x_i} \rightarrow loss$ ,因此;
$\begin{aligned} \frac{\partial l}{\partial \mu_{\mathcal{B}}} &=\frac{\partial l}{\partial \sigma_{\mathcal{B}}^2}\frac{\sigma_{\mathcal{B}}^2}{\partial \mu_{\mathcal{B}}} + \sum_{i=1}^m\frac{\partial l}{\partial \hat{x_i}}\frac{\partial \hat{x_i}}{\partial \mu_{\mathcal{B}}}\\ &=\frac{\partial l}{\partial \sigma_{\mathcal{B}}^2} \frac{-2}{m}\sum_{i=1}^m(x_i-\mu_{\mathcal{B}}) + \sum_{i=1}^m\frac{\partial l}{\partial \hat{x_i}} (\frac{-1}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}})\\ \end{aligned}$
$x_i$ :有3条边,路径: $x_i\rightarrow\mu_{\mathcal{B}}\rightarrow loss$ , $x_i\rightarrow \sigma_{\mathcal{B}}^2\rightarrow loss$ , $x_i\rightarrow \hat{x_i}\rightarrow loss$
$\begin{aligned} \frac{\partial l}{\partial x_{i}} &=\frac{\partial l}{\partial \mu_{\mathcal{B}}} \frac{\partial \mu_{\mathcal{B}}}{\partial x_{i}}+\frac{\partial l}{\sigma_{\mathcal{B}}^{2}} \frac{\sigma_{\mathcal{B}}^{2}}{\partial x_{i}}+\frac{\partial l}{\hat{x}_{i}} \frac{\hat{x}_{i}}{\partial x_{i}} \\ &=\frac{\partial l}{\partial \mu_{\mathcal{B}}} \frac{1}{m}+\frac{\partial l}{\partial \sigma_{\mathcal{B}}^{2}} \frac{-2}{m}\left(x_{i}-\mu_{\mathcal{B}}\right)+\frac{\partial l}{\partial \hat{x}_{i}} \frac{1}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \end{aligned}$

求导完毕!!!
附上代码实现:

def batchnorm_forward(x, gamma, beta, bn_param):
    """
    Forward pass for batch normalization.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
    - mode: 'train' or 'test'; required
    - eps: Constant for numeric stability
    - momentum: Constant for running mean / variance.
    - running_mean: Array of shape (D,) giving running mean of features
    - running_var Array of shape (D,) giving running variance of features

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    
    if mode == 'train':

        sample_mean = np.mean(x, axis=0)
        sample_var = np.var(x, axis=0)
        out_ = (x - sample_mean) / np.sqrt(sample_var + eps)

        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var

        out = gamma * out_ + beta
        cache = (out_, x, sample_var, sample_mean, eps, gamma, beta)

    elif mode == 'test':

        scale = gamma / np.sqrt(running_var + eps)
        out = x * scale + (beta - running_mean * scale)

    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache

def batchnorm_backward(dout, cache):
    """
    Backward pass for batch normalization.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from batchnorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None

    out_, x, sample_var, sample_mean, eps, gamma, beta = cache

    N = x.shape[0]
    dout_ = gamma * dout
    dvar = np.sum(dout_ * (x - sample_mean) * -0.5 * (sample_var + eps) ** -1.5, axis=0)
    dx_ = 1 / np.sqrt(sample_var + eps)
    dvar_ = 2 * (x - sample_mean) / N

    # intermediate for convenient calculation
    di = dout_ * dx_ + dvar * dvar_
    dmean = -1 * np.sum(di, axis=0)
    dmean_ = np.ones_like(x) / N

    dx = di + dmean * dmean_
    dgamma = np.sum(dout * out_, axis=0)
    dbeta = np.sum(dout, axis=0)

    return dx, dgamma, dbeta

2. Batch Normalization的效果及其证明

(一) 减小Internal Covariate Shift的影响, 权重的更新更加稳健.
对于不带BN的网络,当权重发生更新后,神经元的输出会发生变化,也即下一层神经元的输入发生了变化.随着网络的加深,该影响越来越大,导致在每一轮迭代训练时,神经元接受的输入有很大的变化,此称为Internal Covariate Shift. 而BatchNormalization通过归一化和仿射变换(平移+缩放),使得每一层神经元的输入有近似的分布.
假设某一层神经网络为:
$\mathbf{H_{i+1}} = \mathbf{W} \mathbf{H_i} + \mathbf{b}$
对权重的导数为:
$\frac{\partial l}{\partial \mathbf{W}} = \frac{\partial l}{\partial \mathbf{H_{i+1}}} \mathbf{H_i}^T$
对权重进行更新:
$\mathbf{W} \leftarrow\mathbf{W} - \eta \frac{\partial l}{\partial \mathbf{H_{i+1}}} \mathbf{H_i}^T$
可见,当上一层神经元的输入( $\mathbf{H_i}$ )变化较大时,权重的更新变化波动大.
(二)batch Normalization具有权重伸缩不变性,可以有效提高反向传播的效率,同时还具有参数正则化的效果.
记BN为:
$Norm(\mathbf{Wx}) = = \mathbf{g} \cdot \frac{\mathbf{W} \mathbf{x}-\mu}{\sigma}+\mathbf{b}$
为什么具有权重不变性? $\downarrow$
假设权重按照常量 $\lambda$ 进行伸缩,则其对应的均值和方差也会按比例伸缩,于是有:
$\begin{aligned} Norm\left(\mathbf{W}^{\prime} \mathbf{x}\right) &= \mathbf{g} \cdot \frac{\mathbf{W}^{\prime} \mathbf{x}-\mu^{\prime}}{\sigma^{\prime}}+\mathbf{b}\\&=\mathbf{g} \cdot \frac{\lambda \mathbf{W} \mathbf{x}-\lambda \mu}{\lambda \sigma}+\mathbf{b}\\ &= \mathbf{g} \cdot \frac{\mathbf{W} \mathbf{x}-\mu}{\sigma}+\mathbf{b}\\ &=Norm(\mathbf{W} \mathbf{x}) \end{aligned}$

为什么能提高反向传播的效率? $\downarrow$
考虑权重发生伸缩后,梯度的变化:
为方便(公式打累了),记 $\mathbf{y}=Norm(\mathbf{Wx})$
$\begin{aligned} \frac{\partial l}{\partial \mathbf{x}} &= \frac{\partial l}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{x}}\\ &=\frac{\partial l}{\partial \mathbf{y}} \frac{\partial (\mathbf{g} \cdot \frac{\mathbf{W} \mathbf{x}-\mu}{\sigma}+\mathbf{b}))}{\partial \mathbf{x}}\\ &=\frac{\partial l}{\partial \mathbf{y}} \frac{\mathbf{g}\cdot\mathbf{W}}{\sigma}\\ &=\frac{\partial l}{\partial \mathbf{y}} \frac{\mathbf{g}\cdot \lambda\mathbf{W}}{\lambda\sigma} \end{aligned}$
可以发现,当权重发生伸缩时,相应的 $\sigma$ 也会发生伸缩,最终抵消掉了权重伸缩的影响.
考虑更一般的情况,当该层权重较大(小)时,相应 $\sigma$ 也较大(小),最终梯度的传递受到权重影响被减弱,提高了梯度反向传播的效率.同时, $g$ 也是可训练的参数,起到自适应调节梯度大小的作用.

为什么具有参数正则化的作用? $\downarrow$
计算对权重的梯度:
$\begin{aligned} \frac{\partial l}{\partial \mathbf{W}} &= \frac{\partial l}{\partial \mathbf{y}} \frac{\partial\mathbf{y}}{\partial\mathbf{W}}\\ &=\frac{\partial l}{\partial \mathbf{y}} \frac{\partial(\mathbf{g} \cdot \frac{\mathbf{W} \mathbf{x}-\mu}{\sigma}+\mathbf{b})}{\partial \mathbf{W}}\\ &=\frac{\partial l}{\partial \mathbf{y}} \frac{\mathbf{g}\cdot \mathbf{x}^T}{\sigma} \end{aligned}$
假设该层权重较大,则相应 $\sigma$ 也更大,计算出来梯度更小,相应地, $\mathbf{W}$ 的变化值也越小,从而权重的变化更为稳定.但当权重较小时,相应 $\sigma$ 较小,梯度相应会更大,权重变化也会变大.

3. 为什么要加 $\gamma$ , $\beta$

为了保证模型的表达能力不会因为规范化而下降.
如果激活函数为Sigmoid,则规范化后的数据会被映射到非饱和区(线性区),仅利用到线性变化能力会降低神经网络的表达能力.
如果激活函数使用的是ReLU,则规范化后的数据会固定地有一半被置为0.而可学习参数 $\beta$ 能通过梯度下降调整被激活的比例,提高了神经网络的表达能力.

经过归一化后再仿射变换,会不会跟没变一样?
首先,新参数的引入,将原来输入的分布囊括进去,而且能表达更多的分布;
其次, $\mathbf{x}$ 的均值和方差和浅层的神经网络有复杂的关联,归一化之后变成 $\hat{\mathbf{x}}$ ,再进行仿射变换 $\mathbf{y}=\mathbf{g} \cdot \hat{\mathbf{x}}+\mathbf{b}$ ,能去除与浅层网络的密切耦合;
最后新参数可以通过梯度下降来学习,形成利于模型表达的分布.

Turtlelin007

关注

3
点赞
踩
3

收藏

觉得还不错? 一键收藏
2
评论
深度学习归一化方法[一] Batch Normalization

文章目录Batch Normalization1. Batch Normalization原理2. Batch Normalization的效果及其证明3. 为什么要加$\gamma$,$\beta$论文: https://arxiv.org/pdf/1502.03167.pdfBatch Normalization对模型的初始输入进行归一化处理，可以提高模型训练收敛的速度;对神经网络内层的...
复制链接

扫一扫