Stochastic Approximation 随机近似方法的详解之（三）Dvoretzky’s convergence theorem

定理内容

Theorem 6.2 (Dvoretzky’s Theorem). Consider a stochastic process
$w_{k+1}=\left(1-{\alpha }_k\right)w_k+{\beta }_k{\eta }_k$,
其中 { α k } k = 1 ∞ , { β k } k = 1 ∞ , { η k } k = 1 ∞ \{\alpha_k\}^\infty_{k=1},\{\beta_k\}^\infty_{k=1},\{\eta_k\}^\infty_{k=1} {αk​}k=1∞​,{βk​}k=1∞​,{ηk​}k=1∞​都是随机序列。这里${\alpha }_k\ge 0,{\beta }_k\ge 0$ 对于所有的$k$都是成立的。那么 $w_k$ would converge to zero with probability 1 if the following conditions are satisfied:

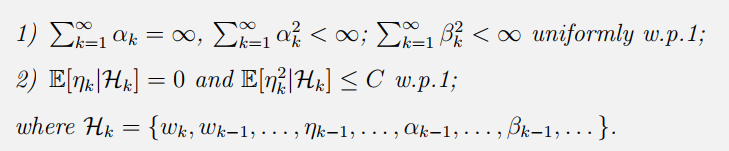
要点阐释

1. RM算法里面的${\alpha }_k$是确定性的。然而Dvoretzky’s Theorem中 ${\alpha }_k,{\beta }_k$ 可以是由${\mathcal{H}}_k$决定的随机变量。因此Dvoretzky’s Theorem 更加通用和强大。
2. 对于uniformly w.p.1 的解释：
   
3. 不再要求观测误差项${\eta }_k$的系数${\beta }_k$的收敛速度了，收敛的快也没有关系。
   

证明在这里不展开，需要用到quasimartingales的知识

应用

证明Robbins-Monro theorem：

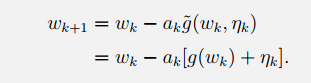
我们在等式两边同时减去目标根：
$w_{k+1}-w^{\ast }=w_k-w^{\ast }-a_k\left[g\left(w_k\right)-g\left(w^{\ast }\right)+{\eta }_k\right]$

然后就有：（注意，下面用到了中值定理）

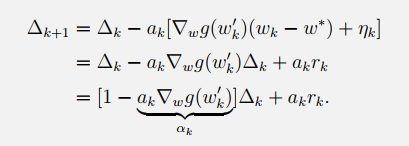
注意这里的${\alpha }_k$不再是确定的了，而是由$w_k和w_k^{\prime }$共同决定的随机序列。对照Dvoretzky’s convergence theorem成立的条件，发现都满足：

到这里也就证明了RM算法求解方程根的收敛性。

定理的扩展：

原定理只能解决单变量的问题，不够使啊。必须扩展一下，让它可以处理多变量。扩展后的Dvoretzky’s convergence theorem 可以用来分析一些随机迭代算法的收敛性：比如Q-learning和TD算法。

扩展后的定理的内容：

在这样的定义下，原先数值上的大小比较就变成了不同向量之间的max norm的比较。注意哈，${\mathcal{H}}_k$是历史数据序列。

顺便解释一下max norm：

定理扩展的一些说明

1. 扩展后的定理比原定理更加通用。首先，由于最大范数（the maximum norm）的引入，它可以处理多元变量的情况，对于具有很多个状态的强化学习问题，这一点很重要。第二，相比于原定理对$\mathbb{E}\left[e_k(x)\mid {\mathcal{H}}_k\right]=0$ and $\mathrm{var}\left[e_k(x)\mid {\mathcal{H}}_k\right]\le C$的要求，this theorem only requires that the expectation and variance are bounded by the error ∆k。
2. 虽然(6.9)只是针对单个状态，但它可以处理多个状态的原因是是因为条件3和4，它们是针对整个状态空间的。此外, 在应用该定理证明RL算法的收敛性时，我们需要表明(6.9)对每个状态都有效。

参考
https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning