参数是如何更新的

参数是如何更新的

二层模型

线性回归：

我们有$n$个样本，每个样本有$k$个属性即$k$元。
对于第$j$个样本的所有属性$x_i$，其组织方式假设是：

$A_j=A_j(x_i;w_i,b)={\sum }_{i=0}^k(w_i\ast x_i)+b$；

矩阵写法：$A_j={\mathbf{W}}^{\mathbf{T}}\mathbf{X}$;
$A_j$并不是矩阵，而是一个标量。
我们称$A_j$为属性函数（仅笔者这么称呼）。
属性函数还有其他形式吗？

• MaxPooling层：从$l$个属性值，选择最大的一个，$0\leqq l\leqq k$；
• MeanPooling层：对$l$个属性值求平均，$0\leqq l\leqq k$；
• Dropout层：随机丢掉/保留一部分属性；
• 全连接层：$A_j=A_j(x_i;w_i,b)={\sum }_{i=0}^l(w_i\ast x_i)+b$，$0\leqq l\leqq k$；可以看清全连接的本质了！
• 卷积层：$A_j=A_j(x_i;w_i,b)={\sum }_{i=0}^l(w_i\ast x_i)+b$，$0\leqq l\leqq k$；可以看清卷积的本质了！

当k=1，即一元线性回归；
当k>1，即多元线性回归。

我们的假设函数是线性的，即$H_j(input)=a\ast input+v$
1、这里的$input$是什么？$input$就是$A_j$
2、$a$和$v$又是什么？假设函数的参数。
$H_j=H(A_j)=a\ast ({\sum }_{i=0}^k(w_i\ast x_i)+b)+v$
$={\sum }_{i=0}^k(a{w}_i\ast x_i)+(ab+v)$
令$a\ast w_i=w_i$，$ab+v=b$，或理解成$a=v=1$，则有：
$H_j={\sum }_{i=0}^k(w_i\ast x_i)+b$

或者假设函数就是$H(input)=input$
可以看到假设函数与属性函数是一模一样的。虽然如此，我们要明白“一元线性”中“一元”和“线性”的含义，这里的线性不是指属性函数是线性的（虽然属性函数是线性的），而是指假设函数是线性的。

还有哪里我们对属性函数采用线性操作？
在神经网络中，$A_j$为卷积层或全连接层的时候，后面会有激活函数，激活函数一般我们会选择非线性的，比如Sigmoid、ReLU，最后一层全连接多分类情况激活函数选择Softmax，二分类情况选择Sigmoid。而$A_j$为Pooling层或Dropout层的时候，一般都没有显式指出激活函数，但是不代表没有，而是其激活函数$H_j=H(A_j)=A_j$，所以这里就是线性的。

假设函数=逻辑回归中的判别函数Sigmoid=神经网络中隐层激活函数=神经网络中输出层的softmax函数，他们的本质上都是一样的。所以下文中，激活函数也用$H$来表示。

损失函数/目标函数：
这里使用均方误差MSE为例：
$L=\frac{1}{n}{\sum }_{j=0}^n(H_j-y_j{)}^2$；
$=\frac{1}{n}[(H_0-y_0{)}^2+...+(H_n-y_n{)}^2]$；
以一元线性回归为例$x_j$是指第$j$个样本的$x$属性,$n$表示样本数：
$L=\frac{1}{n}[((w\ast x_0+b)-y_0{)}^2+...+((w\ast x_n+b)-y_n{)}^2]$；
如果是3元，$x_{ji}$表示第$j$个样本的第$i$个属性，损失函数是这样的：
$L=\frac{1}{n}[((w0\ast x_{00}+w1\ast x_{01}+w2\ast x_{02}+b)-y_0{)}^2+...+((w0\ast x_{n0}+w1\ast x_{n1}+w2\ast x_{n2}+b)-y_n{)}^2]$；

也可以在$L$上乘以$\frac{1}{2}$简化求导。

可见，如果我们对$w_i$求偏导会有求和的过程$\sum$。

损失函数求导：
可以看出$L$是复合函数，我们可以使用链式法则（复合函数求导利器）进行求导：

$\frac{\partial L}{\partial w_i}=\frac{2}{n}{\sum }_{j=0}^n(\frac{\partial L}{\partial H(w_i)}\ast \frac{\partial H_j}{\partial A_j}\ast \frac{\partial A_j}{\partial w_i})$
其中：
$\frac{\partial L}{\partial H_j}=H_j-y_j$

$\frac{\partial H_j}{\partial A_j}=a$

$\frac{\partial A_j}{\partial w_i}=x_{ji}$

所以$\frac{\partial L}{\partial w_i}=\frac{2}{n}{\sum }_{j=0}^n((H_j-y_j)\ast a\ast x_{ji})$

我们不妨让a=v=1，则：$\frac{\partial L}{\partial w_i}=\frac{2}{n}{\sum }_{j=0}^n((H_j-y_j)\ast x_{ji})$

同理：$\frac{\partial L}{\partial b}=\frac{2}{n}{\sum }_{j=0}^n((H_j-y_j)\ast 1)$

使用梯度下降进行参数更新：
$w_i=w_i+\eta \ast \frac{\partial L}{\partial w_i}$
$=w_i+\eta \ast \frac{2}{n}{\sum }_{j=0}^n((H_j-y_j)\ast a\ast x_{ji})$

$b=b+\eta \ast \frac{\partial L}{\partial b}$
$=b+\eta \ast \frac{2}{n}{\sum }_{j=0}^n((H_j-y_j)\ast 1)$

注意观察上面参数更新的式子，由3部分组成：$\eta$、$H_j-y_j$和$x_{ji}$，其中$\eta$是超参数学习率，$Res=H_j-y_j$称为残差，即假设函数的输出与真实样本标记之差，$x_{ji}$是样本$j$的第$i$个特征值。

如果$n=1$，就是随机梯度下降法SGD；
如果$n=$所有样本数，就是批梯度下降法BGD；
如果$1<n<$所有样本数，就是小批梯度下降法MBGD；

####################################################

逻辑回归
属性函数$A_j={\sum }_{i=0}^k(w_i\ast x_i)+b$

假设函数$H_j=\frac{1}{1+e^{-A_j}}$

损失函数：交叉熵损失函数
极大似然估计（Maximum Likelihood Estimation，MLE）角度理解：
$MLE=\frac{1}{n}{\prod }_{j=0}^n(H_j^{y_j}\ast (1-H_j{)}^{1-y_j})$
$n$表示样本数；
对MLE做等价变形：两边同时取对数
$L=\frac{1}{n}{\sum }_{j=0}^n(y_j\ast log(H_j)+(1-y_j)\ast log(1-H_j))$
损失函数$L$越大，证明我们得到的$w_i,b$越好，我们习惯损失函数越小越好，所以对右边取负：
$L=-\frac{1}{n}{\sum }_{j=0}^n(y_j\ast log(H_j)+(1-y_j)\ast log(1-H_j))$

损失函数求导：
对参数$w_i$求偏导:
$\frac{\partial L}{\partial w_i}=-\frac{1}{n}{\sum }_{j=0}^n(\frac{\partial L}{\partial H_j}\ast \frac{\partial H_j}{\partial A_j}\ast \frac{\partial A_j}{\partial w_i})$

其中：

$\frac{\partial L}{\partial H_j}=y_j\ast \frac{1}{H_j}+(1-y_j)\ast \frac{1}{1-H_j}\ast (-1)$

$\frac{\partial H_j}{\partial A_j}=H_j\ast (1-H_j)$

$\frac{\partial A_j}{\partial w_i}=x_{ji}$

所以：
$\frac{\partial L}{\partial w_i}=-\frac{1}{n}{\sum }_{j=0}^n((y_j\ast \frac{1}{H_j}-(1-y_j)\ast \frac{1}{1-H_j})\ast H_j\ast (1-H)\ast x_{ji})$
$=-\frac{1}{n}{\sum }_{j=0}^n((y_j\ast (1-H_j)-(1-y_j)\ast H_j)\ast x_{ji})$
$=\frac{1}{n}{\sum }_{j=0}^n((H_j-y_j)\ast x_{ji})$

同理：$\frac{\partial L}{\partial b}=\frac{1}{n}{\sum }_{j=0}^n((H_j-y_j)\ast 1)$

可以看到最后的结果和线性回归使用均分误差作为损失函数求导得到的结果是一样的，区别在于假设函数$H$不一样了。

使用梯度下降进行变量更新不再累述，同样，n决定了使用的是SGB、BGD还是MBGD。

多层模型

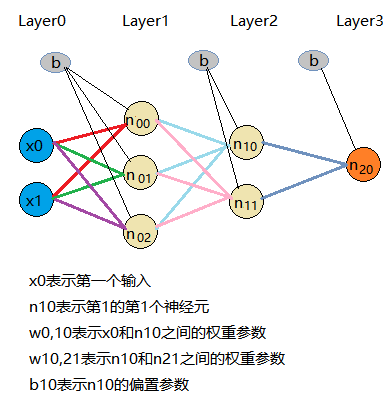
多层网络中，每一层的输出都是特征/属性/元。有最原始的$x_0$、$x_1$等到各个神经元的输出（神经元的输出就是神经元对应激活函数的输出）都是属性。既然是属性，那么其组织方式都是：
$A_{l,s}={\sum }_{i=0}^k(w_{is}\ast x_i)+b_{l,s}$；
$A_{l,s}$表示对应第$l$层的第$s$个神经元的输入，$l\ge 0$，$s\ge 0$；
那么第$l-1$层有$k$个输出（即有$k$个属性到下一层）。
$w_{is}$表示第$l-1$层的第$i$个神经元与第$l$层的第$s$个神经元之间的权重参数；

激活函数：$H_{l,s}=\frac{1}{1+e^{-A_{l,s}}}$
$H_{l,s}$表示对应第$l$层的第$s$个神经元的输出，$l\ge 0$，$s\ge 0$；

输入样本$j$，其有$k=2$个属性，那么网络是怎么传播的？
神经元$n_{10}$
  输入：$A_{1,0}=w_{00,10}\ast x_0+w_{01,10}\ast x_1+b_{1,0}$
  输出：$H_{1,0}=H(A_{1,0})=\frac{1}{1+e^{-A_{1,0}}}$
神经元$n_{11}$的输入与输出略；
神经元$n_{12}$的输入与输出略；

神经元$n_{20}$的输入：
$A_{2,0}=w_{10,20}\ast H_{1,0}+w_{11,20}\ast H_{1,1}+w_{12,20}\ast H_{1,2}+b_{2,0}$
神经元$n_{20}$的输出：$H_{2,0}=H(A_{2,0})$

神经元n21的输入与输出略。

神经元n30的输入：
$A_{3,0}=w_{20,30}\ast H_{2,0}+w_{21,30}\ast H_{2,1}+b_{3,0}$
神经元n30的输出：$H_{3,0}=H(A_{3,0})$
上面就是前向/前馈传播(Feed-Forward)。

损失函数，以交叉熵损失函数为例：
$L=-\frac{1}{n}{\sum }_{j=0}^n(y_j\ast log(H_o)+(1-y_j)\ast log(1-H_o))$

$n$表示样本数；$H_o$表示样本$j$的输出层的输出；如果输出层有多个神经元，如多分类任务中最后一层的激活函数使用softmax，是将特征值限定在[0,1]之间，这样$H_o$和$y_j$都是向量。

要更新隐层与输出层之间的参数，可以求偏导如下：
$\frac{\partial L}{\partial w_o}=-\frac{1}{n}{\sum }_{j=0}^n(\frac{\partial L}{\partial H_o}\ast \frac{\partial H_o}{\partial A_o}\ast \frac{\partial A_o}{\partial w_o})$

隐层到输出层之间的参数的更新比较好理解，和两层模型的参数更新一样。那么我们如果更新隐层之间以及输出层和隐层之间的参数呢？之所以有这样的难题是因为损失函数就是作用在输出层上的即$H_o-y_j$才有意义。可是隐层上又不能使用损失函数$L$，那么怎么求导并更新参数呢？如果我们把目给聚集在链式求导公式上：

$\frac{\partial L}{\partial H_o}\ast \frac{\partial H_o}{\partial A_o}\ast \frac{\partial A_o}{\partial w_o}$

我们可以把上面的公式拆分成3部分：

$\frac{\partial L}{\partial H_o}$ 即损失函数对输出函数（假设函数/激活函数）的求导

$\frac{\partial H_o}{\partial A_o}$ 即输出函数（假设函数/激活函数）对输入函数（属性函数）的求导

$\frac{\partial A_o}{\partial w_o}$ 即输入函数（属性函数）对参数的求导

上面3个部分中，只有第1个部分使用了损失函数$L$。第2部分我们可以改成$\frac{\partial H_l}{\partial A_l}$ 即l层的输出函数对输入函数的求导，第3部分我们可以改成$\frac{\partial A_l}{\partial w_l}$即l层的输入函数对参数的求导。重点看第1部分：
${\sigma }_o=\frac{\partial L}{\partial H_o}$
如果是均方误差损失函数：$\sigma =H-y$
如果是交叉熵损失函数：$\sigma =y\ast \frac{1}{H}-(1-y)\ast \frac{1}{1-H}$
可以看出$\sigma$代表的就是误差，所以反向/逆传播指的就是误差逆传播，即传播的是$\sigma$。

那么误差是怎么逆传播的？
误差的产生也不都是最后一层造成的，前面各层也会后贡献。所以我们要按照各神经元的权重反馈给各个神经元，那么第$l$层的第$s$个神经元的误差：

${\sigma }_{l,s}={\sum }_{i=0}^k(w_{is}\ast {\sigma }_{l+1,i})+b_{l,s}$

其中$w_{is}$表示第$l+1$层的第$i$个神经元与第$l$层的第$s$个神经元之间的权重；b_{l,s}第$l$层的第$s$个神经元的偏置；σ_{l+1,i}表示第$l+1$层的第$i$个神经元的误差，显然这里$l$不为输出层；

对比误差函数${\sigma }_{l,s}$和属性函数$A_{l,s}={\sum }_{i=0}^k(w_{is}\ast x_i)+b_{l,s}$；可以看出两者是相同的，只是误差函数是对$l+1$层的误差进行加权求和，而属性函数是对$l-1$层的属性/特征进行加权求和。

至此，我们就得到：
第$l-1$层的第$i$个神经元与第$l$层的第$s$个神经元之间的权重参数$w_{is}$的更新公式：
注意：
  我们求${\sigma }_{l,s}$的时候使用的是第$l$层和第$l+1$层之间的权重参数；更新的参数是第$l-1$层和第$l$层之间的权重参数。

$w_{is}=w_{is}+\eta \ast ({\sigma }_{l,s}\ast \frac{\partial H_{l,s}}{\partial A_{l,s}}\ast \frac{\partial A_{l,s}}{\partial w_{is}})$

其中
${\sigma }_{l,s}$来自于$l+1$层，误差由上一层传播而来；

$\frac{\partial H_{l,s}}{\partial A_{l,s}}$来自于$l$层，对$l$层的激活函数求导；

$\frac{\partial A_{l,s}}{\partial w_{is}}=H_{l-1,i}$ 来自于$l-1$层，即第$l-1$层第i个神经元的输出；

第$l$层的第$s$个神经元之间的偏置参数$b_s$的更新公式：
$b_s=b_s+\eta \ast ({\sigma }_{l,s}\ast \frac{\partial H_{l,s}}{\partial A_{l,s}}\ast 1)$

梯度弥散与梯度爆炸问题(待完善)
如果激活函数$H$为Sigmoid函数，那么：
$\frac{\partial H_{l,s}}{\partial A_{l,s}}=H_{l,s}\ast (1-H_{l,s})$

  $\because 0\leqq H_{l,s}\leqq 1$
  $\therefore 0\leqq H_{l,s}\ast (1-H_{l,s})\leqq 1$

总结：文中通过简单的线性回归、二分类等常见机器学习算法，引申至神经网络，使得神经网络参数的更新不再神秘，且使得BP算法更加容易理解！

https://zhuanlan.zhihu.com/p/91675218