理解线性回归中的常数项

如何理解线性回归中的常数项

线性模型

线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即：

f(x)=w1x1+w2x2+…+wdxd+b+e

很容易理解，b是常数项，代表的是截距，而e是误差。

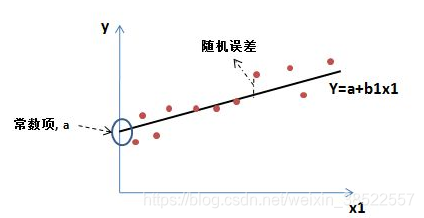
以上图像代表的是一元线性模型，而多元线性模型则使用更多的自变量去描述因变量。
从一元线性模型入手，我们可以发现：
1）误差是实际的数据点和我们回归模型之间的差值，并不一定，有大有小，符合正态分布的规律。
2）常数项解释的是，不被自变量所解释的，长期稳定存在的非随机部分，也可称为信息残留。

常数项的存在帮助我们解决了一个问题：当所有的自变量为0的时候，因变量是什么？然而这样的解释仅具有数学意义。
所谓的拟合过程，追求的是残差项的均值为0，且残差项的平方和最小。以此规则计算得出的各项参数，可以使得一条拟合曲线在我们的数据点中浮动，并最终找到一个位置，是的残差项的均值为0。此时，我们的截距就是常数项。可以说这是对解释变量留下的偏误进行线性修正。本身并不具备可以理解的现实意义。
另外，常数项也被这样解读，它是一个恒为1的虚拟变量的参数。这帮助我们利用了本可能被忽略的因素。
而且，残差项未必总是按标准正态分布，如果它们的均值不为0，而存在一个期望，事实上这个期望会被包括在常数项之中。帮助我们修正这正太分布的均值，使之为0。