双复合摆的动力学【牛顿法---拉格朗日法】两种方式

最新推荐文章于 2024-04-06 14:41:32 发布

JianRobSim

最新推荐文章于 2024-04-06 14:41:32 发布

阅读量1.1w

点赞数 8

分类专栏：机器人运动方程推导与应用

本文链接：https://blog.csdn.net/weixin_39090239/article/details/116378491

版权

机器人运动方程推导与应用专栏收录该内容

11 篇文章 ¥39.90 ¥99.00

订阅专栏

本文详细介绍了双复合摆的运动方程推导，分别采用牛顿法和拉格朗日法。在牛顿法中，详细讨论了双摆的模型参数、运动方程、反作用力方程，并通过MATLAB进行计算验证。在拉格朗日法部分，阐述了动能与势能的概念，推导了欧拉拉格朗日运动方程，并最终解耦出摆角加速度。所有理论推导与Simscape Multibody模型进行了对比，确保了理论的准确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、双摆运动方程的牛顿法推导

0、前言

在此示例中，我们将导出并实现双复合摆的运动方程【在重力和粘性力作用下的双摆运动】。具体来说，我们将要：

（1）使用牛顿法推导运动方程；（2）推导施加到摆杆上的反作用力。

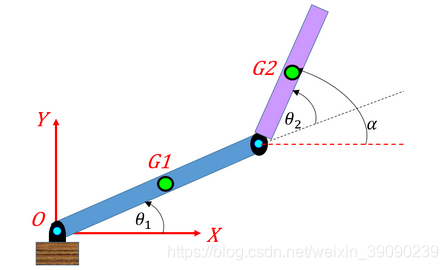
1、定义link1和link2的模型参数

syms L1X_s    L2X_s 
syms m1_s     m2_s
syms t 
syms   theta1(t)  TH1_s  TH1D_s TH1DD_s
syms    alpha(t)  ALP_s  ALPD_s ALPDD_s

2、运动方程

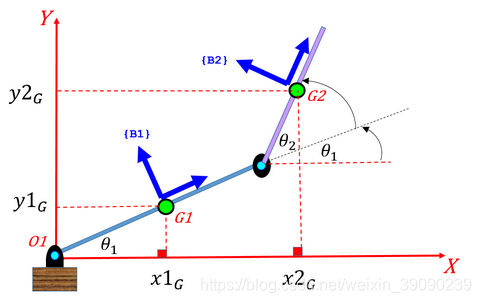
接下来，我们应用牛顿第二定律，并推导该系统的动态运动方程。我们将假定每个枢轴点都会有粘性阻尼。下面显示系统图-重力沿负Y方向起作用。

3、link2运动和反作用力方程

取关于link2 的质心的力矩总和：

还考虑作用在质心（固定坐标系）X方向和Y方向上的力：【link2质心位置x2G,y2G；可得到速度和加速度】

现在，让我们使用MATLAB定义一些表达式后用于计算：

定义：

X2_G        = L1X_s*cos(theta1) + (L2X_s/2)*cos(alpha);%质心在X方向上的位置分量
X2_G_d      = diff(X2_G, t) %质心速度X方向
X2_G_dd     = diff(X2_G, t, 2)%质心加速度X方向

定义：

Y2_G        = L1X_s*sin(theta1) + (L2X_s/2)*sin(alpha);%质心在Y方向上的位置分量
Y2_G_d      = diff(Y2_G, t) %质心速度Y方向
Y2_G_dd     = diff(Y2_G, t, 2) %质心加速度Y方向

现在计算得到：，根据如下公式。

R2_X = m2_s*X2_G_dd;
R2_Y = m2_s*Y2_G_dd  + m2_s*9.81;

然后将SYMFUN转换为SYMS

THE_R2_X  = formula(R2_X); % R2_X(t);
THE_R2_Y  = formula(R2_Y); % R2_Y(t);

进行一些变量替换：

our_OLD_list_1 = [theta1,  diff(theta1,1),   diff(theta1, 2)];
our_new_list_1 = [ TH1_s,          TH1D_s,           TH1DD_s];

our_OLD_list_2 = [alpha,    diff(alpha,1),    diff(alpha, 2)];
our_new_list_2 = [ALP_s,           ALPD_s,           ALPDD_s];

THE_R2_X  = subs( THE_R2_X, [our_OLD_list_1, our_OLD_list_2], ...
                            [our_new_list_1, our_new_list_2]);
                          
THE_R2_Y  = subs( THE_R2_Y, [our_OLD_list_1, our_OLD_list_2], ...
                            [our_new_list_1, our_new_list_2]);

RESULT_THE_R2_X = THE_R2_X;
RESULT_THE_R2_Y = THE_R2_Y;

4、Link1运动和反作用力方程

取绕枢轴点O1的力矩之和：

还考虑作用在惯性（固定坐标系）X方向和Y方向上的力：

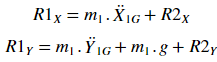
当查看Link1的受力图时，会看到R2力的作用。正是这些R2力提供了“连接”两个link运动的约束。使用“约束”一词，因为R2力是函数

定义下面的表达式用于计算:

X1_G        = (L1X_s/2)*cos(theta1);
X1_G_d      = diff(X1_G, t);
X1_G_dd     = diff(X1_G, t, 2); 

Y1_G        = (L1X_s/2)*sin(theta1);
Y1_G_d      = diff(Y1_G, t);
Y1_G_dd     = diff(Y1_G, t, 2);

计算

syms R2X_s R2Y_s
R1_X = m1_s*X1_G_dd  + R2X_s;
R1_Y = m1_s*Y1_G_dd  + R2Y_s + m1_s*9.81;

然后将SYMFUN转换为SYMS，

THE_R1_X  = formula(R1_X); % R1_X(t);
THE_R1_Y  = formula(R1_Y); % R1_Y(t);

进行一些变量替换：

our_OLD_list_1 = [theta1,  diff(theta1,1),   diff(theta1, 2)];
our_new_list_1 = [ TH1_s,          TH1D_s,           TH1DD_s];

THE_R1_X  = subs( THE_R1_X, [our_OLD_list_1], ...
                            [our_new_list_1])
                          
THE_R1_Y  = subs( THE_R1_Y, [our_OLD_list_1], ...
                            [our_new_list_1])

RESULT_THE_R1_X = THE_R1_X;
RESULT_THE_R1_Y = THE_R1_Y;

创建simulink块R1和R2方程。首先看一下每个方程式内的符号：

symvar(  RESULT_THE_R2_X  )  
symvar(  RESULT_THE_R2_Y  )
symvar(  RESULT_THE_R1_X  )  
symvar(  RESULT_THE_R1_Y  )

创建：

tf_i_should_create_SL_block = true;
if(true==tf_i_should_create_SL_block)
    MODEL_NAME = 'bh_tmp_model_for_newt';
    if(4==exist(MODEL_NAME))
        close_system(MODEL_NAME, 0);
        delete(MODEL_NAME);
    end
     new_system(MODEL_NAME)
    open_system(MODEL_NAME)      
    
    % the R1X and R1Y equations
    INPUT_VAR_ORDER = {'L1X_s', 'm1_s', 'R2X_s','R2Y_s'...
                      'TH1DD_s', 'TH1D_s', 'TH1_s'}; 
                  
    matlabFunctionBlock( [MODEL_NAME,'/THE_R1_forces'], ...
                         RESULT_THE_R1_X, RESULT_THE_R1_Y, ...
                        'Optimize',false, ...
                        'Vars', INPUT_VAR_ORDER, ...
                        'Outputs', {'R1_X','R1_Y'}   );
                     
    % the R2X and R2Y equations
    INPUT_VAR_ORDER = {'L1X_s',  'L2X_s',  'm2_s', ...
                      'TH1DD_s', 'TH1D_s', 'TH1_s', ...
                      'ALPDD_s', 'ALPD_s', 'ALP_s'}; 
                  
    matlabFunctionBlock( [MODEL_NAME,'/THE_R2_forces'], ...
                         RESULT_THE_R2_X, RESULT_THE_R2_Y, ...
                         'Optimize',false, ...
                         'Vars', INPUT_VAR_ORDER, ...
                         'Outputs', {'R2_X','R2_Y'}   );              
end

在此基础构建的simulink模型中构建模型。

link1取绕枢轴点O1的力矩之和：为了分离出theta1_DD

link2取绕枢轴点O2的力矩之和：为了分离出theta2_DD

初始化一些参数：

density = 1000; % kg/m3
L1x     = 1.00; % m
L1y     = 0.050; % m
L1z     = 0.005; % m
mass1   = density * L1x*L1y*L1z; % kg
I1g      = mass1*(L1x^2 + L1y^2)/12;
I1o      = I1g + mass1*(L1x/2)^2;

L2x     = 0.5; % m
L2y     = 0.05; % m
L2z     = 0.005; % m
mass2   = density * L2x*L2y*L2z; % kg
I2g      = mass2*(L2x^2 + L2y^2)/12;
I2o      = I2g + mass2*(L2x/2)^2;

b1_damp = 0.005; %0.1 (N.m/(rad/sec));
b2_damp = 0.005; %0.1 (N.m/(rad/sec));
g = 9.80665;  % m/sec^2

theta1_0     = 45*pi/180;                    % rad
theta1_dot_0 = 0;                            % rad/sec 
theta2_0     = 30*pi/180;                    % rad
theta2_dot_0 = 0;                            % rad/sec
alpha_0      = theta1_0 + theta2_0;          % rad
alpha_dot_0  = theta1_dot_0 + theta2_dot_0;  % rad/sec

加载到MATLAB工作区中。除了实现我们的手推运动方程式之外，我们还创建了具有相同两连杆的Simscape Multibody。推导结果与Simscape模型进行比较，两组结果一致。

simscape模型：

双摆结果：【指定初始位置pose，在重力和粘性阻尼下的双摆运动】

如果加大粘性阻尼：【双摆运动减缓】

%改变粘性阻尼
b1_damp = 0.5; %0.1 (N.m/(rad/sec));
b2_damp = 0.5; %0.1 (N.m/(rad/sec));

二、拉格朗日法推导运动方程：

1、系统方程符号推导

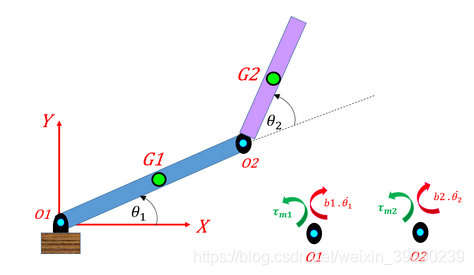
欧拉拉格朗日运动方程：【动能与势能之差】

其中q={theta1，theta2}为，Qk为非保守广义力，T为动能，V为势能。

（1）两个link的速度定义

%link参数 质量，重力加速度，转动惯量
syms m2_s m1_s g_s I1G_s I2G_s
syms L1X_s L2X_s 
syms b1_s  b2_s
syms t theta1(t)  TH1_s  TH1D_s TH1DD_s
syms   theta2(t)  TH2_s  TH2D_s TH2DD_s
%link1质心位置
X1_G        = (L1X_s/2)*cos(theta1(t));
Y1_G        = (L1X_s/2)*sin(theta1(t));
%得到link1质心位置速度和加速度【x方向和y方向平移分量】
X1_G_d      = diff(X1_G, t); 
X1_G_dd     = diff(X1_G, t, 2); 

Y1_G_d      = diff(Y1_G, t); 
Y1_G_dd     = diff(Y1_G, t, 2); 


%link2的质心位置
alpha       = theta1(t) + theta2(t);
X2_G        = L1X_s*cos(theta1(t)) + (L2X_s/2)*cos(alpha);
Y2_G        = L1X_s*sin(theta1(t)) + (L2X_s/2)*sin(alpha);
%得到link2质心位置速度和加速度【x方向和y方向平移分量】
X2_G_d      = diff(X2_G, t)
X2_G_dd     = diff(X2_G, t, 2); 

Y2_G_d      = diff(Y2_G, t); 
Y2_G_dd     = diff(Y2_G, t, 2);

（2）定义系统动能【平动动能+旋转动能】

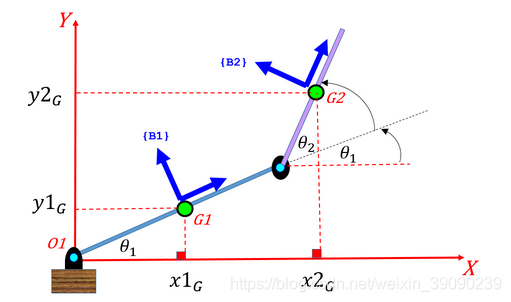
%平动动能；与非平面二自由度双摆处可以对照看看。
KE_trans = 0.5*m1_s*( X1_G_d^2  + Y1_G_d^2) + ...
           0.5*m2_s*( X2_G_d^2  + Y2_G_d^2);
%旋转转动动能
theta1_d   = diff(theta1, t);
theta2_d   = diff(theta2, t);

KE_rot   = 0.5*I1G_s*( (theta1_d           )^2 ) + ...
           0.5*I2G_s*( (theta1_d + theta2_d)^2 );
%总动能
KE = KE_trans + KE_rot;

（3）定义系统势能

%系统势能，仅重力
PE = m1_s*g_s*Y1_G  +  m2_s*g_s*Y2_G;

（3）系统拉格朗日算子

L_ORIGINAL = KE - PE;
symvar(  L_ORIGINAL  )

现在，我们要做的就是根据拉格朗日方程式进行一系列偏导计算：

为了方便获得拉格朗日偏导数，做如下符号集的对应替换。

syms q_1  q_1p  q_2   q_2p
L = subs(L_ORIGINAL,  [theta1(t), diff(theta1(t),t),...  
                       theta2(t),diff(theta2(t),t)], ...
                       [  q_1, q_1p, q_2, q_2p]);

（4）推导Q1

处理：

dLdq1p = diff(L, q_1p);%dl/dq1p
%替换符号集
dLdq1p = subs(dLdq1p,  [   q_1,   q_1p,  q_2,    q_2p], ...
   [theta1(t), diff(theta1(t),t),  theta2(t),  diff(theta2(t),t)]);

处理：

der_dt_of_dLdq1p = diff(dLdq1p, t);

处理：

dLdq1 = diff(L, q_1);
%符号替换
dLdq1 = subs(dLdq1,  [q_1,q_1p,q_2,q_2p], ...
 [theta1(t), diff(theta1(t),t),  theta2(t), diff(theta2(t),t)]);

目前为止第一个运动方程：

syms Q1_s
EOM_TH1_LHS = der_dt_of_dLdq1p - dLdq1;
EOM_TH1_LHS = simplify(EOM_TH1_LHS);
EOM_TH1_RHS = Q1_s;
EOM_TH1     = EOM_TH1_LHS == EOM_TH1_RHS;
%简化表达式
simplify(EOM_TH1)

（5）推导Q2：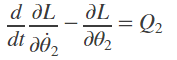

同上Q1的过程：

%符号替换同上
L = subs(L_ORIGINAL, [theta1(t), diff(theta1(t),t),...
                     theta2(t),  diff(theta2(t),t)], ...
                     [q_1,  q_1p,  q_2,  q_2p]);

处理：

dLdq2p = diff(L, q_2p);
dLdq2p = subs(dLdq2p,  [q_1,q_1p,q_2,q_2p], ...
 [theta1(t), diff(theta1(t),t),  theta2(t),  diff(theta2(t),t)]);

处理：

der_dt_of_dLdq2p = diff(dLdq2p, t);

处理：

dLdq2 = diff(L, q_2);
%替换符号
dLdq2 = subs(dLdq2,  [q_1,q_1p,q_2,q_2p], ...
[theta1(t), diff(theta1(t),t),  theta2(t),  diff(theta2(t),t)]);

到此第二次运动方程：

syms Q2_s
EOM_TH2_LHS = der_dt_of_dLdq2p - dLdq2;
EOM_TH2_LHS = simplify( EOM_TH2_LHS );
EOM_TH2_RHS = Q2_s;
EOM_TH2     = EOM_TH2_LHS == EOM_TH2_RHS;
simplify(EOM_TH2)

（5）解耦theta1_DD和theta2_DD

我们可以通过将两个方程都发送到solve（）中来解耦方程，分离出两个加速度。首先，让我们将EOLD表达式（变量的HOLDER列表）替换为EOM表达式：

our_OLD_list_1 = [theta1,  diff(theta1,1),   diff(theta1, 2)];
our_new_list_1 = [ TH1_s,          TH1D_s,           TH1DD_s];

our_OLD_list_2 = [theta2,  diff(theta2,1),   diff(theta2, 2)];
our_new_list_2 = [ TH2_s,          TH2D_s,           TH2DD_s];

EOM_TH1        = subs(EOM_TH1, [our_OLD_list_1, our_OLD_list_2], ...
                               [our_new_list_1, our_new_list_2]);
                      
EOM_TH2        = subs(EOM_TH2, [our_OLD_list_1, our_OLD_list_2], ...
                               [our_new_list_1, our_new_list_2]);

进行分离：

S = solve([EOM_TH1, EOM_TH2],[TH1DD_s, TH2DD_s]);

RESULT_TH1 = S.TH1DD_s;
RESULT_TH2 = S.TH2DD_s;

（6）生成simulink块。得到theta1_DD和theta2_DD。

tf_i_should_create_SL_block = true;
if(true==tf_i_should_create_SL_block)
    MODEL_NAME = 'bh_tmp_model_for_lagr';
    if(4==exist(MODEL_NAME))
        close_system(MODEL_NAME, 0);
        delete(MODEL_NAME);
    end
    new_system(MODEL_NAME)
    open_system(MODEL_NAME)   
    
    % define the INPUT variable order - this is optional
    INPUT_VAR_ORDER = { 'I1G_s', 'I2G_s', ...
                        'L1X_s', 'L2X_s', 'g_s', 'm1_s', 'm2_s', ...
                        'TH1D_s', 'TH1_s', ...
                        'TH2D_s', 'TH2_s', ...
                        'Q1_s', 'Q2_s'};     
                    
    % Put BOTH equations into one block 
    matlabFunctionBlock( [MODEL_NAME,'/THE_THETA_SYS_DD'], RESULT_TH1, RESULT_TH2, ...
                         'Optimize', false, ...
                         'Vars',     INPUT_VAR_ORDER, ...
                         'Outputs', {'theta1_DD', 'theta2_DD'}   );     
end

在此基础上完善simulink模型:【Q1和Q2为非保守力，这里主要是粘性力。在双摆过程中因为重力为保守力做功时与动能相互转换】

初始化模型参数同上：

density = 1000; % kg/m3
L1x     = 1.00; % m
L1y     = 0.050; % m
L1z     = 0.005; % m
mass1   = density * L1x*L1y*L1z; % kg
I1g      = mass1*(L1x^2 + L1y^2)/12;
I1o      = I1g + mass1*(L1x/2)^2;

L2x     = 0.5; % m
L2y     = 0.05; % m
L2z     = 0.005; % m
mass2   = density * L2x*L2y*L2z; % kg
I2g      = mass2*(L2x^2 + L2y^2)/12;
I2o      = I2g + mass2*(L2x/2)^2;

b1_damp = 0.005; %0.1 (N.m/(rad/sec));
b2_damp = 0.005; %0.1 (N.m/(rad/sec));
g = 9.80665;  % m/sec^2

theta1_0     = 45*pi/180;                    % rad
theta1_dot_0 = 0;                            % rad/sec 
theta2_0     = 30*pi/180;                    % rad
theta2_dot_0 = 0;                            % rad/sec
alpha_0      = theta1_0 + theta2_0;          % rad
alpha_dot_0  = theta1_dot_0 + theta2_dot_0;  % rad/sec

同样建立simscape模型，对比结果的一致性。