An example: Ordinal Probit Model

We describe an ordinal Probit model for post-secondary education choice and estiamted a simple model with the dependant variable of interest is PSECHOICE and the explanatory variable is GRADES(Lower numberical value of GRADES indicate better performance). We rank the college possibilities as follows:
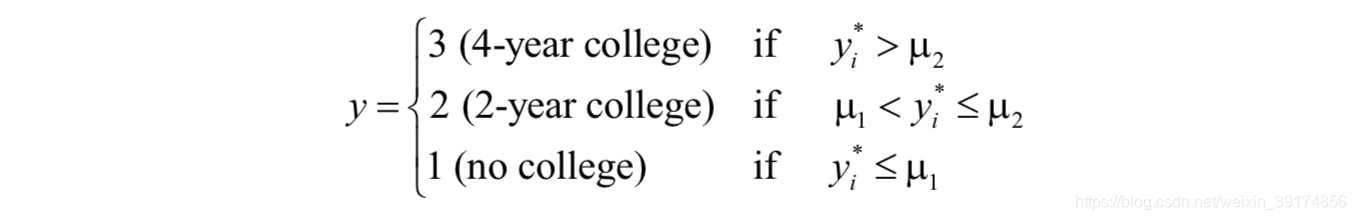The following table shows the ordered Probit estimation results:

1. Based on the estimated results in the above table, comment on the changes for probabilities of “2-year college” group and “no college” group when GRADES increases. Explain if they are consistent with your expectations.
   Answer: when grades increases, the pr of the highest ranked choice (4-year) goes down, and the lowest ranked choice (no college)goes up, but difficult to say about 2 year college according to the formula of group 2. (According to marginal effect formula for group 1, we find that only sign of beta matter since the pdf is alwyas positive. These are consistent with the expectation.)
2. Compute the marginal effect of GRADES on the probability that a student with GRADES = 6 attends 2- year college.
   For Ordered Probit model,
   $$\frac{\partial P[y=2]}{\partial x}=[\varphi ({\mu }_1-\beta x)-\varphi ({\mu }_2-\beta x)]\ast \beta ]=0.0522$$

If we now extend the above ordered Probit model by including other variables: FAMINC-family income in $\pounds$1000, FAMSIZ-number of family menbers; and dummy variables BLACK and PARCOLL=1 if somst educated parent had a college degree, the estimated results is in the Table below.

3. Test the joint significance of the variables added above using a likelihood ratio test.
   $$LR=2(l_U-l_R)=2\ast (-839.86-(-875.82))=71.91$$
   The critical chi-squared value at a 0.05 level of significance is ${\chi }_{(0.95,4)}^2=9.49$. Since the test statistic is greater than the critical value, we reject the null hypothesis and conclude that FAMINC,FAMSIZ,PARCOLL and BLACK are jointly significant and should be included in the model.
4. Compute the probability that a Black student from a household of four members, including a parent who went to college, and household income of $\pounds$52,000, will attend a 4-year college if GRADES= 6.64.
   $$P[y=3]=1-\varphi ({\mu }_2-\beta x)=0.8525$$

Micoeconometrics course, University of LIVERPOOL