双树复小波变换Dual-Tree Complex Wavelet Transform在信号处理中的应用

本文展示了双树复小波变换 (Dual-Tree Complex Wavelet Transforms，DTCWT) 在信号、图像和轴承故障诊断方面的应用。 DTCWT 为两个独立的两通道滤波器组，在实际应用用，不能随意选择两棵树中使用的尺度小波滤波器。第一棵树 {h0 ,h1 } 的低通（尺度）和高通（小波）滤波器生成一个尺度函数和小波，另一棵树是由第一棵树的尺度函数的近似希尔伯特变换以及相应的高通滤波器生成的小波函数组成，记作{g0，g1 }。因此由两棵树形成的复值尺度函数和小波函数是近似解析的，因此，DTCWT比DWT具有更小的移位方差和更大的方向选择性。DTCWT的冗余度明显小于未抽取的DWT 的冗余度。本文验证了 DTCWT 的近似移位不变性，DTCWT在2-D和3-D数据中的方向选择性，以及DTCWT变换在图像去噪等方面的应用。

代码见评论区。

MATLAB环境下双树复小波基础及在轴承故障诊断中的应用
程序运行环境为MATLAB R2021B，主要演示双树复小波基础及在轴承故障诊断中的应用。
算法可迁移至金融时间序列，地震信号，语音信号，声信号，生理信号（ECG,EEG,EMG）等一维时间序列信号及二维图像和三维图像。

擅长现代信号处理(改进小波分析系列，改进变分模态分解，改进经验小波变换，改进辛几何模态分解等等)，改进机器学习，改进深度学习，机械故障诊断，改进时间序列分析(金融信号，心电信号，振动信号等)
 

双树复小波变换DTCWT基本理论

双树复小波变换DTCWT采用二叉树结构的两路滤波器组进行信号的分解和重构，第一棵树生成实部，第二棵生成虚部，合理设计实、虚部树低通滤波器，满足半采样延迟条件，具有近似平移不变性。两树的滤波器采样频率相同，但是它们之间的延迟恰好是一个采样间隔，这样虚部树中第１层的二抽取恰好采到实部树中二抽取所丢掉的采样值，在获得了复小波变换的平移不变性的同时避免了大量的计算并且具有容易实现的优势。下图为３层双树复小波的分解和重构过程。

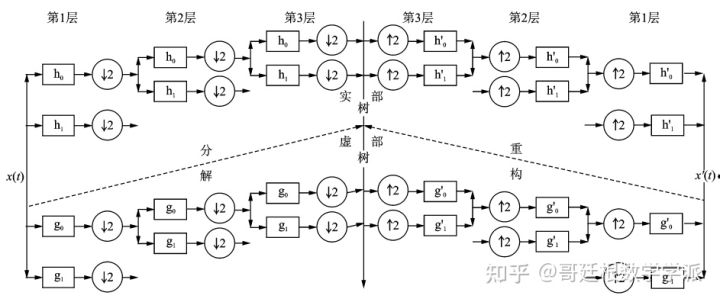
３层双树复小波的分解和重构过程

虚线上方实部树变换的小波系数和尺度系数可由式（2）和（3）计算

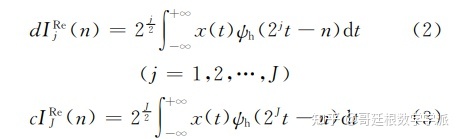
相关的参考文献如下：

[1]Huang Tongyuan,Xu Jia,Yang Yuling,Han Baoru. Robust Zero-Watermarking Algorithm for Medical Images Using Double-Tree Complex Wavelet Transform and Hessenberg Decomposition[J]. Mathematics,2022,10(7).

[2]Zhou Yilu,Fu Xiaojin. Image Denoising Based on Dual-tree Complex Wavelet Transform and Convolutional Neural Network[J]. Journal of Physics: Conference Series,2021,1995(1).

[3]Lei Wang,Zhiwen Liu,Hongrui Cao,Xin Zhang. Subband averaging kurtogram with dual-tree complex wavelet packet transform