在实时图形渲染里, 矩阵变换是计算物体位置,物体形状,光照以及摄像机方向等等重要操作的基本载体。而在矩阵变换中有一种特殊的变换形式--旋转变换。本文将主要介绍旋转变换的基础原理, 不会讲解具体API的应用。
旋转变换有三种主要的表达形式--rotation matrix(旋转矩阵),euler transform(欧拉变换), 和quaternion transform(四元数变换)。本文将对rotation matrix(旋转矩阵),欧拉变换和四元数变换的基本原理,转换关系和适用情况进行介绍。
1.概念介绍及推导原理
Rotation Matrix
在transform中旋转最直接的表现形式,具体原理也很简单:
对于二位坐标中的一个vector V
和原vector比较, 我们有rotation
如果我们回到三维坐标系,如果一个向量V(x,y,z)是关于x轴旋转的,那么对于V来说, x坐标是不会产生变换的, 变换的维度在yz平面上。因此,在homogeneous transform(齐次变换)的homogeneous matrix应该是
矩阵的trace, 对角线元素之和等于
Euler Transform
首先介绍head, pitch, roll的概念。本文将沿用real time rendering 一书中的写法,有的地方也写做roll, pitch, yaw, 图示如下:
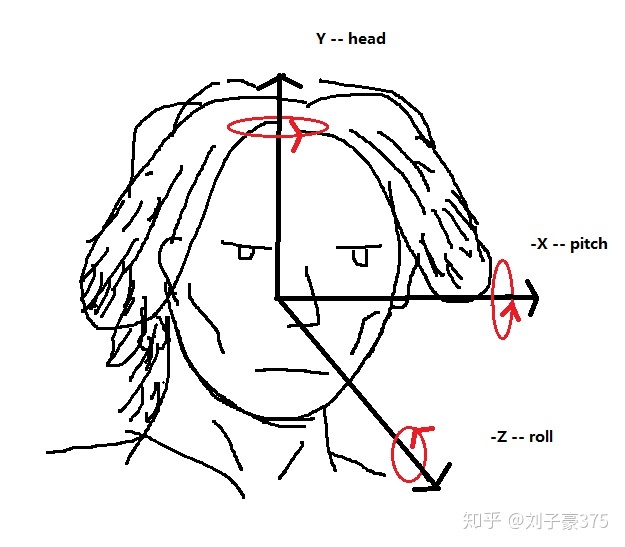
懒得用别人的图写来源就随手图自己画了张:^)
一般情况下,camera都会放在-z上,在world space的坐标为(0,0,-1)。
回到欧拉角当中, 欧拉矩阵将关于三坐标轴的旋转结合在一起,因此有了:
综合上面关于关于各个坐标轴矩阵的计算,有:
=
此时注意h,p,r相乘的顺序为逆序。
由欧拉角转换为matrix3x3的函数也十分简单明了,照搬上述公式即可,不再赘述。
对于设计师来说,欧拉角的优势是直接,在小角度变换时方便,然而欧拉角有一些严重的局限性:
1. gimbal lock: 万向节锁
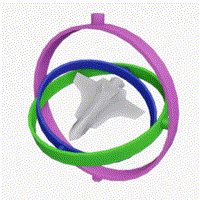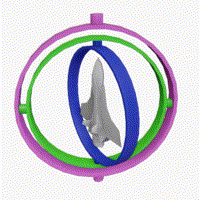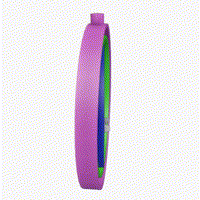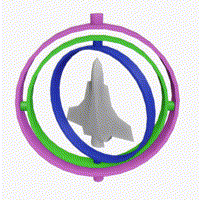
动图来自wikipedia。 这种动图很形象的展示了什么是gimbal lock -- 失去一个维度上的自由度。简单地说,当绿环和粉环对齐时,蓝环和粉环产生的旋转是一样的。这就造成了一个问题,由于我们只锁定了一个旋转维度,本应由三维旋转变成二维,而现在只有一维了,这就叫失去了一个维度上的自由度。
从数学的角度来讲,在上面提到的欧拉矩阵中, 当cosp=0, sinp=1的时候,也就是pitch角度等于
该物体的旋转仅有r+h决定。 然而我们仅确定了一个方向p的角度为90度, 而物体仅有一个旋转物体,因此我们说该物体失去了一个方向上的自由度,也就是gimbal lock。
2.插值问题:由于欧拉角一般由矩阵计算,我们非常的难以进行两组欧拉角之间的插值。在两个矩阵之间进行矩阵的插值变换时非常繁琐的。可见欧拉角的局限性是非常严重的,因此我们提出另外一个概念,quaternion四元数。
Quaternion
quaternion通过旋转轴和围绕这条旋转轴的角度来表示一次旋转。一般情况下相比于欧拉角,把旋转直接转换成quaternion要比变成欧拉角便捷一些。而且,对于运动中的物体,例如摄像机旋转,很多时候都需要进行方向插值(orientation interpolation),也就是在旋转的起点和终点进行插值来获得运动轨迹上每一点(像素点)的变化, 这时采用quaternion要比欧拉角方便许多。
quaternion的定义,一般写作
这条性质很重要。我们在euler angle和quaternion的变换中会用到。
另外,很多quaternion的乘法,加法,共轭等性质很容易查到,就不一一赘述了。
在这里重点只讲一条方便理解quaternion的性质,unit quaternion,也就是单位四元数。
unit quaternion可以写成
在单位向量中,
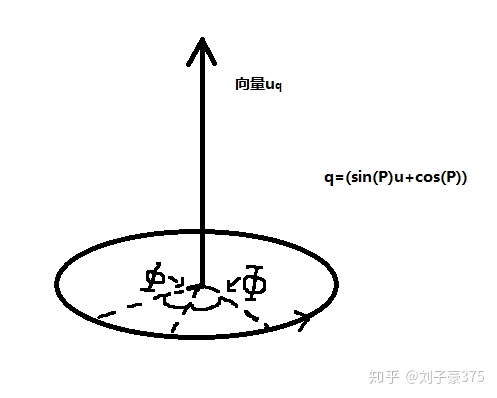
其中
三种旋转表示方法的基本性质就介绍到这里。作为开发者我们常常会遇到三种旋转表示方法之间的转化,以下将介绍三种旋转表示方法之间的转换。
2.Rotation Matrix,Euler Angle和Quaternion之间的相互转换
Euler angle和rotation matrix之间的转化其实上文提过,代码直接照搬上述公式即可。
因为所有的transform,无论是旋转还是平移,最终都要变成4x4矩阵代入到每个vertex的计算当中去,因此quaternion和matrx44之间的转换经常用到,所以先讲quaternion和matrix4x4之间的转化方法。
quaternion->matrix44 先上公式
其中
上代码:
matrix44 简单粗暴。
matrix4x4->quaternion:
首先重要的一点是计算matrix的trace,也就是对角线之和,下面用t代替。
这样我们就得到了
上代码。
inline quaternion toQuaternion(const matrix44& mat) {
float trace = mat[0][0] + mat[1][1] + mat[2][2] + mat[3][3];
float qw = 1.f / 2 * sqrt(trace);
float qx = (mat[2][1] - mat[1][2]) / (4 * qw);
float qy = (mat[0][2] - mat[2][0]) / (4 * qw);
float qz = (mat[1][0] - mat[0][1]) / (4 * qw);
assert(trace > 0);
quaternion ret;
ret.w = qw;
ret.v = vector3f(qx, qy, qz);
return ret;
}注意我这里是放在header文件里所以用了inline。
对于设计和策划来说,欧拉角是一种更直接的表示方法,而对于开发者来说,quaternion的计算更容易,所以两者的转换经常涉及到。
euler angle->quaternion:
对于欧拉角来说,三个方向,我们把每个方向的变换都转化为quaternion,再按照旋转顺序相乘,我们就得到了最终的quaternion。
对于x-pitch方向, 我们有
y-head方向, 我们有
z-roll方向, 我们有
按照
此时注意乘法的方向,从后往前,根据最开始提到的quaternion的基本性质,化简得到:
这样一个quaternion的qw, qx, qy, qz就对应得到了。如果你用到的不同的h,p,r方向,那么对应的结果就会不一样,应该重新计算。
上代码:
quaternion::quaternion(const eulerAngle& ea) {
float cosa, sina, cosb, sinb, cosg, sing;
cosa = std::cos(ea.pitch / 2.f);
sina = std::sin(ea.pitch / 2.f);
cosb = std::cos(ea.head / 2.f);
sinb = std::sin(ea.head / 2.f);
cosg = std::cos(ea.roll / 2.f);
sing = std::sin(ea.roll / 2.f);
w = cosg * cosa * cosb + sing * sina * sinb;
v.x = cosg * sina * cosb - sing * cosa * sinb;
v.y = cosg * cosa * sinb + sing * sina * cosb;
v.z = cosg * sina * sinb + sing * cosa * cosb;
}quaternion->euler angle:
这里我们要用到欧拉变换里的公式:
在这个矩阵中,很容易得到
所以直接通过反三角函数就可以求得其中的值。这里注意,由于
上代码:
eulerAngle::eulerAngle(const quaternion& q) {
float x = q.v.x, y = q.v.y, z = q.v.z, w = q.w;
float e20 = 2.0f * (x * z - w * y);
float e22 = 1.0f - 2.0f * (x * x + y * y);
head = std::atan2(-e20, e22);
float e21 = 2 * (y * z + w * x);
e21 = e21 > 1.0f ? 1.0f : e21;
e21 = e21 < -1.0f ? -1.0f : e21;
pitch = std::asin(e21);
float e01 = 2.0f * (x * y - w * z);
float e11 = 1.0f - 2.0f * (x * x + z * z);
roll = std::atan2(-e01, e11);
}
这里我们跑一跑,确定转换关系是否正确:
eulerAngle ea(0.2f, 0.4f, 1.0f);
quaternion q(ea);
eulerAngle test(q);
std::cout << test << std::endl;
没问题,误差可以接受。
总结
以上就是关于旋转矩阵,欧拉变换和四元数组的基本概念和转换关系的全部内容。下一篇我们将介绍quaternion里面的特殊函数, slerp 插值函数和vectorRotation。




















 6094
6094











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








