stata面板数据单位根检验llc_【干货分享】PVAR模型的stata操作流程（附操作文件）...

作者：alpamber

网址：https://bbs.pinggu.org/thread-6920947-1-1.html

本文仅用于分享交流，不用于任何商业用途，版权归原作者所有，如有侵权敬请后台联系，我们将在第一时间删除。

简单目录：

stata操作界面简介

PVAR的基本操作流程图

第一步输入数据(以导入Excel数据为例)

第二步 调整数据格式

第三步 描述性分析

第四步 面板单位根检验

第五步 协整检验

第六步 确定最优滞后阶数

第七步 格兰杰因果检验

第八步 GMM估计、脉冲响应及方差分解

stata软件操作界面简介：

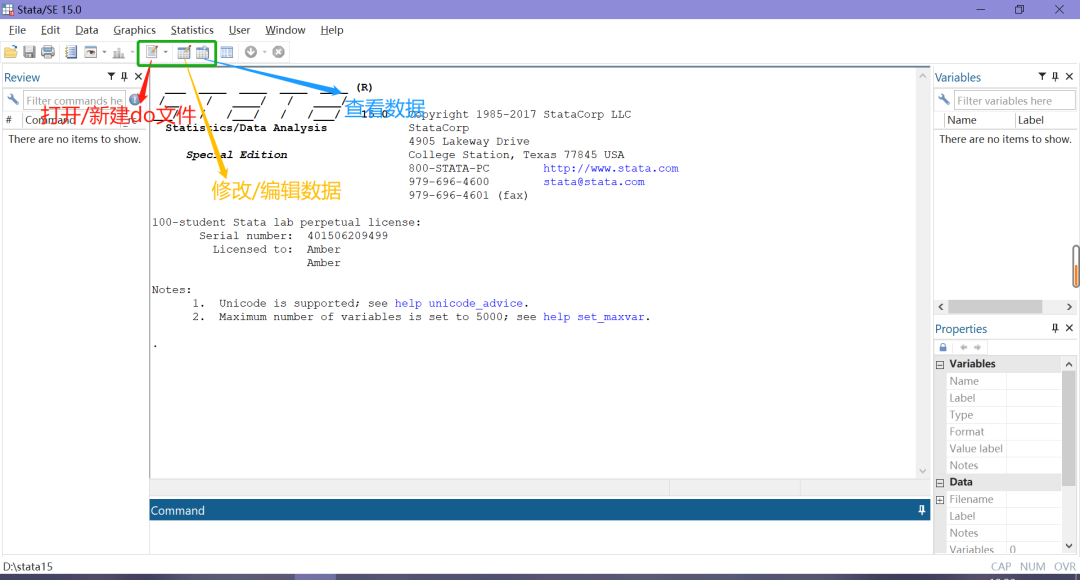
以stata15为例，基本的stata操作界面可以分为六个部分：

最上面两行是菜单，其中比较常用的是第二行中用绿框标出来的三个图标，第一个是新建/打开do文件、第二个是修改/编辑数据、第三个是查看(只读)数据；

    整个界面中间的一大块窗口是结果窗口，执行完命令后的结果就显示在这里；

    结果窗口左边的是Review窗口，记录刚才执行过的所有命令；结果窗口下边的是Command窗口即命令窗口，我们可以在这里输入命令，但一般仅用于输入一些不需要重复的简单的命令，并不常用；结果窗口右边靠上的窗口是Variables(变量)窗口，显示导入数据中包含的各变量信息；结果窗口右边靠下的窗口是Properties窗口，一般在编辑/修改数据时使用。

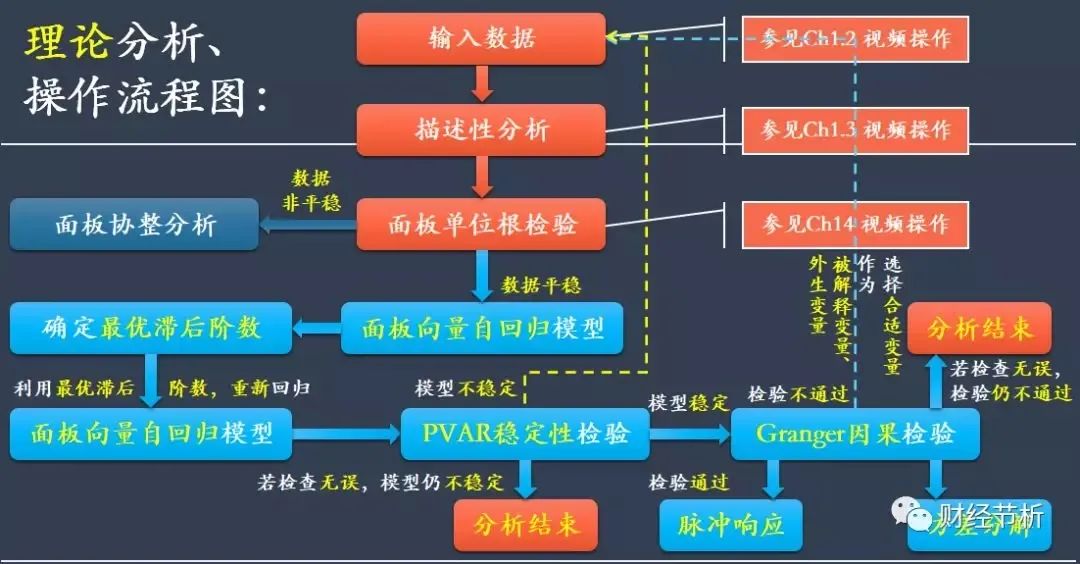
PVAR的基本操作流程图：

第一步 输入数据(以导入Excel数据为例) 在下载安装好stata软件之后，我一般在根目录下新建一个do文件夹，把要导入的Excel文件以及之后的do文件、dta文件和画好的图像都放在这个文件夹里，便于之后在操作过程中的使用和更改。 运用stata软件做PVAR模型，需要运用到许多个命令，为了简便，我们不需要在每一次打开软件操作的时候，都在Command窗口里输入一遍命令，而是将这些命令存入一个do文件，每次在操作前都打开这个do文件，再执行其中的命令。 首先，点击打开/新建do文件的图标，会自动出现一个Untitled.do文件，我们在其中输入或直接复制粘贴命令 import excel d:\stata15\do\ydyl.xlsx, sheet("Sheet1") firstrow 。在这个命令中，import是“导入”命令，excel是导入的文件类型，d:\stata15\do\ydyl.xlsx是导入文件的路径，sheet("Sheet1") 表示导入的是excel文件中的Sheet1，firstrow表示将表格中的第一行数据规定为变量名。需要注意的是，不同于Eviews软件， stata软件是区分大小写的 ，所以在输入路径时，文件名中的大小写一定要注意区分，但是D盘和d盘是一样的。 然后，如下图所示，选中刚才输入的命令，点击菜单中第二行最后一个执行图标，就可以导入以上路径中的数据了。接下来，我们回到stata界面，点击查看数据图标，就可以看到自己导入的数据了。

最后，我们在do文件中，输入或复制粘贴命令save d:\stata15\do\ydyl.dta,replace ，就可以将我们刚刚导入的Excel中的数据，保存为stata软件中的dta文件也就是数据文件了。在这一条命令中，save是“保存”命令，d:\stata15\do\ydyl.dta表示要保存在哪个路径及保存的文件名，replace表示替代之前保存的ydyl.dta文件。如果之前没有保存过这个文件，结果窗口中会提示你没有这个文件，所以第一次保存的时候不用觉得奇怪。

第二步 调整数据格式

1. 打开数据

为了简便，我们不在每一次打开stata软件时，都导入和保存一遍数据，而是运用这样的两条命令：

cd d:\stata15\do    // 指定默认路径

use ydyl.dta,clear   // 打开指定路径下的数据文件

    第一条命令为指定默认路径，第二条命令为打开该默认路径下的数据文件，如果我们不指定路径就直接打开文件的话，系统是无法识别的。

2. 调整格式

    在PVAR模型中，我们导入的数据前两列要分别是个体变量(如地区、国家)和时间变量(如年度、季度、月度)。但是大多时候，我们直接导入进来的数据中，这两列数据的格式不正确的，在stata中无法识别，之后的统计分析中也会出现诸多问题，所以我们要先调整数据格式。正常情况下，个体变量的数据类型应该是long(如地区一=1、地区二=2…)，时间变量的数据类型应该是float，如下图所示，我们可以在查看数据界面右下角的Properties窗口中看到。