逻辑代数01律的理解_抽象代数学习笔记（八）

如同上一篇笔记末尾所说的，从这个部分开始，我们暂时跳过环的部分内容介绍格这种代数结构。

说实话，对于群、环、域，从高中起就有所耳闻，故在系统地学习之前已了解得不少。然而对于格，其就显得陌生许多。然而，我还是发现在格论中同样有着一些很有趣的结果。格论在现实中的一个重要应用就是Boole代数了，故当我们对格论中的一些定理摸不着头脑时或者难以直观地理解时，有时从0-1的Boole代数的角度理解可能会带给我们一些启发。

在正式开始之前，需要先声明读者需要对于偏序关系、极大元、极小元、最大元、最小元、链、反链、Hasse图、可比性等集合论重要概念有着基本的区分与理解。虽然在易错之处我仍旧会多加注解，但是我不再在文中给出其严格定义。

另：文中若无特别说明，默认

为格，

为偏序关系（满足自反性、反对称性、传递性）。

首先，我们从给出格的定义开始。

定义：

对于偏序集

，若对于

的最大下界与最小上界都存在，则

构成格，简记为

。

同时记

的最大下界为

，最小上界为

。

注意：

的最大下界指的是其

下界组成的集合中的最大元，而 最大元必须与集合中的任意一个元素可比。故最大下界需要满足与下界集合中的任意一个元素都可比。

我们一般都会用Hasse图直观地表示一个偏序集。因此，从Hasse图来直观地判断一个偏序集是否为格是一项很重要的技能。

但是这并不是一件简单的事，因为我们需要对任意两个不同元素都验证其最大下界以及最小上界的存在性。

我们列举几例：

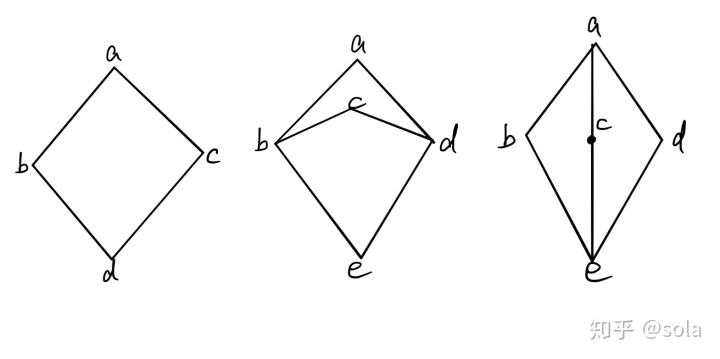
最左侧Hasse图为格，容易验证任意两个点的最小上界与最大下界存在。

但是中间的Hasse图并不为格。考虑

，其上界集为

，然而

不可比，故上界集不存在最小元，

不存在，不为格。

读者容易验证最右侧的Hasse图为格，其被称为钻石格，在后续笔记中会更深入介绍。

与群论中类似地，我们也可以定义子格作为格的子代数。

定义：

非空且

关于最大下界与最小上界运算封闭，则

为

的子格。

在上图最左侧的格中，显然

都为子格，但是注意到