目录
1 马尔可夫链简介
谷歌用于确定搜索结果顺序的算法,称为PageRank,就是一种马尔可夫链。在卷积网络出现之前,HMM马尔可夫模型也是语音处理的常用方法。
在机器学习算法中,马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链(Markov chain),又称离散时间马尔可夫链(discrete-time Markov chain),因俄国数学家安德烈·马尔可夫(俄语:Андрей Андреевич Марков)得名,为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用。
马尔科夫链是指数学中具有马尔科夫性质的离散事件随机过程。在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点,每一步可以移动到任何一个相邻的点,在这里移动到每一个点的概率都是相同的(无论之前漫步路径是如何的)。
下图中有两种状态:A和B。如果我们在A,接下来可以过渡到B或留在A。如果我们在B,可以过渡到A或者留在B。在这张图中,从任意状态到任意状态的转移概率是0.5。

真正的建模工作者不会总是就画一张马尔科夫链图。 相反,他们会使用“转移矩阵”来计算转移概率。状态空间中的每个状态都会出现在表格中的一列或者一行中。矩阵中的每个单元格都告诉你从行状态转换到列状态的概率。因此,在矩阵中,单元格做的工作和图中的箭头所示是一样。在状态转移矩阵中,行和列都是可能的所有状态,对应位置就是已知行状态,转移到列状态的概率。

如果状态空间添加了一个状态,我们将添加一行和一列,向每个现有的列和行添加一个单元格。 这意味着当我们向马尔可夫链添加状态时,单元格的数量会呈二次方增长。因此,转换矩阵就起到了很大的作用(除非你想把法尔科夫链图画的跟丛林一样)。
2 一个经典的马尔科夫链实例
用一句话来概括马尔科夫链的话,那就是某一时刻状态转移的概率只依赖于它的前一个状态。举个简单的例子,假如每天的天气是一个状态的话,那个今天是不是晴天只依赖于昨天的天气,而和前天的天气没有任何关系。这么说可能有些不严谨,但是这样做可以大大简化模型的复杂度,因此马尔科夫链在很多时间序列模型中得到广泛的应用,比如循环神经网络RNN,隐式马尔科夫模型HMM等。
假设状态序列为![]() ,由马尔科夫链定义可知,时刻
,由马尔科夫链定义可知,时刻![]() 的状态只与
的状态只与![]() 有关,用数学公式来描述就是:
有关,用数学公式来描述就是:
![]()
既然某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔科夫链的模型就定了。看一个具体的例子。
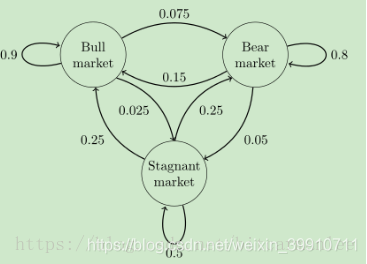
这个马尔科夫链是表示股市模型的,共有三种状态:牛市(Bull market), 熊市(Bear market)和横盘(Stagnant market)。每一个状态都以一定的概率转化到下一个状态。比如,牛市以0.025的概率转化到横盘的状态。这个状态概率转化图可以以矩阵的形式表示。如果我们定义矩阵P某一位置P(i, j)的值为P(j|i),即从状态i变为状态j的概率。另外定义牛市、熊市、横盘的状态分别为0、1、2,这样我们得到了马尔科夫链模型的状态转移矩阵为:

当这个状态转移矩阵P确定以后,整个股市模型就已经确定!
3 状态转移矩阵
从上面的例子不难看出来,整个马尔可夫链模型的核心是状态转移矩阵P。那这个矩阵P有一些什么有意思的地方呢?接下来再看一下。
以股市模型为例,假设初始状态为t0=[0.1,0.2,0.7] ,然后算之后的状态。
def markov():
init_array = np.array([0.1, 0.2, 0.7])
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = init_array
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print i, "\t", res
restmp = res
markov()
最终输出的结果:
0 [ 0.295 0.3425 0.3625]
1 [ 0.4075 0.38675 0.20575]
2 [ 0.4762 0.3914 0.1324]
3 [ 0.52039 0.381935 0.097675]
4 [ 0.55006 0.368996 0.080944]
5 [ 0.5706394 0.3566873 0.0726733]
6 [ 0.58524688 0.34631612 0.068437 ]
7 [ 0.59577886 0.33805566 0.06616548]
8 [ 0.60345069 0.33166931 0.06487999]
9 [ 0.60907602 0.32681425 0.06410973]
10 [ 0.61321799 0.32315953 0.06362248]
11 [ 0.61627574 0.3204246 0.06329967]
12 [ 0.61853677 0.31838527 0.06307796]
13 [ 0.62021037 0.31686797 0.06292166]
14 [ 0.62144995 0.31574057 0.06280949]
15 [ 0.62236841 0.31490357 0.06272802]
16 [ 0.62304911 0.31428249 0.0626684 ]
17 [ 0.62355367 0.31382178 0.06262455]
18 [ 0.62392771 0.31348008 0.06259221]
19 [ 0.624205 0.3132267 0.0625683]
20 [ 0.62441058 0.31303881 0.06255061]
21 [ 0.624563 0.31289949 0.06253751]
22 [ 0.624676 0.3127962 0.0625278]
23 [ 0.62475978 0.31271961 0.06252061]
24 [ 0.6248219 0.31266282 0.06251528]
从第18次开始,状态就开始收敛至[0.624,0.312,0.0625]。最终数字上略有不同,只是计算机浮点数运算造成的罢了。
如果我们换一个初始状态t0 ,比如[0.2,0.3.0.5] ,继续运行上面的代码,只是将init_array变一下,最后结果为:
0 [ 0.35 0.38 0.27]
1 [ 0.4395 0.39775 0.16275]
2 [ 0.4959 0.39185 0.11225]
3 [ 0.53315 0.378735 0.088115]
4 [ 0.558674 0.365003 0.076323]
5 [ 0.5766378 0.3529837 0.0703785]
6 [ 0.5895162 0.34322942 0.06725438]
7 [ 0.59886259 0.33561085 0.06552657]
8 [ 0.6056996 0.32978501 0.06451539]
9 [ 0.61072624 0.32538433 0.06388944]
10 [ 0.61443362 0.32208429 0.06348209]
11 [ 0.61717343 0.31962047 0.0632061 ]
12 [ 0.61920068 0.31778591 0.06301341]
13 [ 0.62070185 0.31642213 0.06287602]
14 [ 0.62181399 0.31540935 0.06277666]
15 [ 0.62263816 0.31465769 0.06270415]
16 [ 0.62324903 0.31410005 0.06265091]
17 [ 0.62370187 0.31368645 0.06261168]
18 [ 0.62403757 0.31337972 0.06258271]
19 [ 0.62428645 0.31315227 0.06256128]
20 [ 0.62447096 0.31298362 0.06254542]
21 [ 0.62460776 0.31285857 0.06253366]
22 [ 0.62470919 0.31276586 0.06252495]
23 [ 0.62478439 0.31269711 0.0625185 ]
24 [ 0.62484014 0.31264614 0.06251372]
到第18次的时候,又收敛到了[0.624,0.312,0.0625] ,这个转移矩阵就厉害了。不管我们的初始状态是什么样子的,只要状态转移矩阵不发生变化,当n→∞ 时,最终状态始终会收敛到一个固定值。
在矩阵分析,自动控制原理等过程中,经常会提到矩阵的幂次方的性质。我们也看看这个状态转移矩阵P 的幂次方有什么有意思的地方?
def matrixpower():
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = transfer_matrix
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print i, "\t", res
restmp = res
matrixpower()
代码运行的结果:
0 [[ 0.8275 0.13375 0.03875]
[ 0.2675 0.66375 0.06875]
[ 0.3875 0.34375 0.26875]]
1 [[ 0.7745 0.17875 0.04675]
[ 0.3575 0.56825 0.07425]
[ 0.4675 0.37125 0.16125]]
2 [[ 0.73555 0.212775 0.051675]
[ 0.42555 0.499975 0.074475]
[ 0.51675 0.372375 0.110875]]
3 [[ 0.70683 0.238305 0.054865]
[ 0.47661 0.450515 0.072875]
[ 0.54865 0.364375 0.086975]]
4 [[ 0.685609 0.2573725 0.0570185]
[ 0.514745 0.4143765 0.0708785]
[ 0.570185 0.3543925 0.0754225]]
5 [[ 0.6699086 0.2715733 0.0585181]
[ 0.5431466 0.3878267 0.0690267]
[ 0.585181 0.3451335 0.0696855]]
6 [[ 0.65828326 0.28213131 0.05958543]
[ 0.56426262 0.36825403 0.06748335]
[ 0.5958543 0.33741675 0.06672895]]
7 [[ 0.64967099 0.28997265 0.06035636]
[ 0.5799453 0.35379376 0.06626094]
[ 0.60356362 0.33130471 0.06513167]]
8 [[ 0.64328888 0.29579253 0.06091859]
[ 0.59158507 0.34309614 0.06531879]
[ 0.60918588 0.32659396 0.06422016]]
9 [[ 0.63855852 0.30011034 0.06133114]
[ 0.60022068 0.33517549 0.06460383]
[ 0.61331143 0.32301915 0.06366943]]
10 [[ 0.635052 0.30331295 0.06163505]
[ 0.60662589 0.3293079 0.06406621]
[ 0.61635051 0.32033103 0.06331846]]
11 [[ 0.63245251 0.30568802 0.06185947]
[ 0.61137604 0.32495981 0.06366415]
[ 0.61859473 0.31832073 0.06308454]]
12 [[ 0.63052533 0.30744922 0.06202545]
[ 0.61489845 0.32173709 0.06336446]
[ 0.6202545 0.31682232 0.06292318]]
13 [[ 0.62909654 0.30875514 0.06214832]
[ 0.61751028 0.31934817 0.06314155]
[ 0.62148319 0.31570774 0.06280907]]
14 [[ 0.62803724 0.30972343 0.06223933]
[ 0.61944687 0.3175772 0.06297594]
[ 0.6223933 0.3148797 0.062727 ]]
15 [[ 0.62725186 0.31044137 0.06230677]
[ 0.62088274 0.31626426 0.062853 ]
[ 0.62306768 0.31426501 0.06266732]]
16 [[ 0.62666957 0.31097368 0.06235675]
[ 0.62194736 0.31529086 0.06276178]
[ 0.62356749 0.31380891 0.0626236 ]]
17 [[ 0.62623785 0.31136835 0.0623938 ]
[ 0.6227367 0.31456919 0.06269412]
[ 0.62393798 0.31347059 0.06259143]]
18 [[ 0.62591777 0.31166097 0.06242126]
[ 0.62332193 0.31403413 0.06264394]
[ 0.62421263 0.31321968 0.0625677 ]]
19 [[ 0.62568045 0.31187792 0.06244162]
[ 0.62375584 0.31363743 0.06260672]
[ 0.62441624 0.31303361 0.06255015]]
20 [[ 0.6255045 0.31203878 0.06245672]
[ 0.62407756 0.31334332 0.06257913]
[ 0.62456719 0.31289565 0.06253716]]
21 [[ 0.62537405 0.31215804 0.06246791]
[ 0.62431608 0.31312525 0.06255867]
[ 0.62467911 0.31279335 0.06252754]]
22 [[ 0.62527733 0.31224646 0.06247621]
[ 0.62449293 0.31296357 0.0625435 ]
[ 0.62476209 0.3127175 0.06252042]]
23 [[ 0.62520562 0.31231202 0.06248236]
[ 0.62462404 0.3128437 0.06253225]
[ 0.62482361 0.31266126 0.06251514]]
24 [[ 0.62515245 0.31236063 0.06248692]
[ 0.62472126 0.31275483 0.06252391]
[ 0.62486922 0.31261956 0.06251122]]
从第20次开始,结果开始收敛,并且每一行都为[0.625,0.312,0.0625] 。
4 马尔可夫链细致平稳条件
首先,马尔科夫链要能收敛,需要满足以下条件:
1.可能的状态数是有限的。
2.状态间的转移概率需要固定不变。
3.从任意状态能够转变到任意状态。
4.不能是简单的循环,例如全是从x到y再从y到x。
以上是马尔可夫链收敛的必要条件。
假设有一个概率的单纯形向量v0,例如我们前面的例子[0.2,0.3.0.5],有一个概率转移矩阵P,例如我们前面的例子:

其中,v0 每个元素的取值范围为[0,1],并且所有元素的和为1。而 P 的每一行也是个概率单纯形向量。由前面的例子我们不难看出,当v0 与P 的n次幂相乘以后,发现得到的向量都会收敛到一个稳定值,而且此稳定值与初始向量v0无关!
那么所有的转移矩阵P 都有这种现象嘛?或者说满足什么样的条件的转移矩阵P 会有这种现象?
细致平衡条件(Detailed Balance Condition):给定一个马尔科夫链,分布π 和概率转移矩阵P,如果下面等式成立
![]()
则此马尔科夫链具有一个平稳分布(Stationary Distribution)。
证明过程比较简单:

上式取j→∞ ,就可以得到矩阵表达式:
![]()
5 马尔可夫链收敛性质
如果一个非周期的马尔可夫链收敛,有状态转移矩阵P,并且任何两个状态都是连通的,那么![]() 为一定值,且与i无关。
为一定值,且与i无关。
![]()

π是方程πP=π 的唯一非负解,其中:
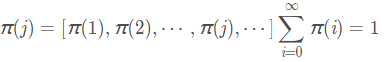
6 应用
马尔可夫链在实际中有非常广泛的应用。例如奠定互联网基础的PageRank算法,就是由马尔可夫链定义的。如果N 是已知网页的数量,一个页面i 有ki 个链接到这个页面,那么它到链接页面的转换概率为![]() ,到未链接页面的概率为
,到未链接页面的概率为![]() ,参数α 的取值大约是0.85。
,参数α 的取值大约是0.85。
另外像语音识别中的HMM隐马尔可夫模型,也在实际中使用非常多,并且在DNN问世之前一直都是语音识别领域中最主流的方法。
小白都能看懂的马尔可夫链详解:https://blog.csdn.net/bitcarmanlee/article/details/82819860


























 5551
5551

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








