三角形周长最短问题_谈“最短”

尊敬的各位家长，大家晚上好，我是成都领川外国语学校初中数学黄老师。非常开心，今天晚上能和家长一起分享我对数学的联想，今天我的讲座内容是令学生非常头痛的数学几何最值问题。为何遇到这种最值问题会头痛，为何有的学生都临近中考了还不能做这种类型的，原因何在。是因为学生没有在脑海里形成模型思想，在做题时不能抽离出题中的基本模型。每年中考都会考最值问题，只要出现几何最值问题，往往得分率很低。真的有那么难吗？其实也未必，今天我将带来大家一起来探索几何最值问题。

1

首先，我想问家长们一个问题，如图

A代表你的家，B代表学校，从家去学校一共有三条路，两条黑色的曲线的路，一条红色的直线的路，抛去路况，堵车等一切问题。你会选择哪条路？

我想这个问题不需要任何的纠结，当然选红色那条路。看都看得出来，这个问题，反映了数学的一个基本事实：两点之间的所有连线段中，线段最短。这个问题是七年级上期第四章《基本平面图形》中的。而由这个基本事实却引发了一连串的问题，我们来看问题起源：唐朝诗人李欣的诗《古从军行》开头两句说：“白日登山望峰火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题。

如图所示：

诗中将军在观望烽火之后从山脚下的A点出发，走到河边饮马后 . 再到B点宿营．请问怎样走才能使总的路程最短？这个问题早在古罗马时代就有了，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？从此，这个被称为“将军饮马”的问题广泛流传．这个问题是七年级下期第五章《简单的轴对称图形》的知识，解决它并不难。

如图所示：

从A出发向河岸引垂线，垂足为D，在AD的延长线  取A关于河岸的对称点A‘，连结A’B，与河岸线相交于C，则C点就是饮马的地方，将军只要从A出发，沿直线走到C，饮马之后，再由C沿直线走到B，走的路程就是最短的。如果将军在河边的另外任一点C‘饮马，所走的路程就是AC’+C‘B，但是，AC'+C'B＝A'C'+C'B＞A'B＝A'C+CB＝AC+CB。

可见，在C点外任何一点C'饮马，所走的路程都要远一些。而这里就相当于是从A‘到B点，路程何时最短，当然是：两点之间，线段最短。

在平时的学生学习过程之中。学生需要能抓住此问题的基本知识点与本质规律提炼归类成简单的解题模型。让学生能在解题过程中通过套用这简单的知识模块,来解决各种各样变化莫测的、复杂的问题。让解题由难变易,化繁为简，学生掌握起来也就更筒单!简单总结将军饮马前两个基本模型：

1.如图，直线 l 和 l 的异侧两点 A . B ，在直线 l 上求作一点 P ，使 PA + PB 最小。 

2. 如图，直线 l 和 l 的同侧两点 A . B ，在直线 l 上求作一点 P ，使 PA + PB 最小。(这也被称为两定一动问题)

下面让我们一起看看这个将军饮马模型的变迁及其延伸:

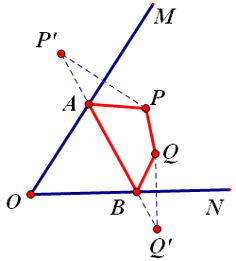
3. 如图，点 P 是 ∠ MON 内的一点，分别在 OM ， ON 上作点 A ， B ，使 △ PAB 的周长最小。也就是PA+AB+PB值最小.通过作图后，不难发现， PA+AB+PB= P1A+AB+P2B=P1P2.而这当中的原理就是：两点之间，线段最短。(这要被称为一定两动问题)

 4. 如图，点P ，Q 为 ∠ MON 内的两点，分别在 OM ， ON 上作点A，B。使四边形PAQB的周长最小。也就PA+AB+BQ+QP值最小。我们可以如图所示的作图，发现PA+AB+BQ+QP=P1A+AB+BQ1+QP=P1P2+PQ。因为PQ是定值，所以周长就最短了，原理依然是：两点之间，线段最短。(这也被称为两定两动问题)

5. 如图，点 A 是 ∠ MON 外的一点，在射线 ON 上作点 P ，使 PA 与点 P 到射线 OM 的距离之和最小。也就是PA+PB最小。通过作图不难发现：PA+PB=AB，这是因为：垂线段最短。 

6.如图，点 A 是 ∠ MON 内的一点，在射线 ON 上作点 P ，使 PA 与点 P 到射线 OM 的距离之和最小。也就是PA+PB值最小。通过作图不难发现：PA+PB=PA1+PB=A1B，这是因为：垂线段最短。(这也被称为一定两动问题) 

以上就是将军饮马的六种常见模型；记住模型后，可以用一句话来概括几何最值问题：过定点作动点所在直线的对称点，再连线或作垂线。(连线的原理是：两点之间，线段最短；作垂线的原理是：垂线段最短)

那这些模型在题目中是怎么呈现的喃？

常见题目  

Part 1. 三角形 

1 ．如图，在等边 △ ABC 中，AB  = 6 ，AD ⊥ BC ，E 是 AC上的一点，M是 AD上的一点，AE =2，求 EM + EC的最小值。 

思考，学生如果能抽离这道题是一定两动问题，便能非常轻松的知道作定点C关于动点M所在直线AD的对称点，然后再作垂线。

有了第一题的铺垫，下面这道中考题就不难了。这是八年级学生必须掌握的问题。

2 ．如图，在锐角△ABC中，AB  = ，∠ BAC ＝ 45°，∠BAC的平分线交BC于点D ，M 、N分别是 AD和 AB上的动点，则 BM + MN的最小值是 ____ ． 

解：作点 B   关于 AD   的对称点 B ' ，过点 B ' 作 B ' E ⊥ AB   于点 E ，交 AD   于点 F ，则线段 B ' E 长就是 BM ＋ ＭＮ 的最小值在等腰 Rt △ AEB ' 中，根据勾股定理得到， B ' E  = 4

同样的，在正方形中还可以这样呈现

Part 2. 正方形 

2 ．如图所示，正方形 ABCD   的面积为 12 ， △ ABE   是等边三角形，点 E   在正方形 ABCD   内，在对角线 AC   上有一点 P ，使 PD ＋ PE   的和最小，则这个最小值为(   )  

解：即在 AC   上求一点 P ，使 PE + PD   的值最小。

点 D 关于直线 AC的对称点是点 B ，连接 BE交 AC于点 P ，则 BE= PB +PE =PD + PE ，BE的长就是 PD + PE的最小值 BE = AB  =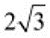 

矩形之中是这样的。

Part 3. 矩形  

1 ．如图，若四边形 ABCD   是矩形，   AB  = 10 cm ， BC  = 20 cm ， E   为边 BC   上的一个动点， P   为 BD   上的一个动点，求 PC + PD   的最小值；  

解：作点C关于 BD的对称点 C '，过点 C ' ，  

作 C ' B ⊥ BC ，交 BD于点 P ，则 C ' E就是 PE + PC的最小值  

直角 △ BCD中，CH = 

直角 △ BCH中，BH =

△ BCC '的面积为：BH × CH=160 

∴   C ' E × BC = 2×160  则 CE ' = 16 

九年级菱形之中也可以这样考

Part 4. 菱形  

1 ．如图，若四边形 ABCD是菱形，AB =10 cm ，∠ABC =45°， E为边 BC上的一个动点， P为 BD上的一个动点，求 PC + PE的最小值；  

解：点C关于 BD的对称点是点 A ，  

过点 A作 AE ⊥BC ，交 BD于点 P ，

则 AE 就是 PE + PC的最小值  

在等腰△EAB中，求得AE的长为 

Part 5. 直角梯形 

1 ．已知直角梯形 ABCD中， AD ∥ BC ，AB ⊥ BC ， AD =2 ，BC = DC =5 ，点 P在 BC上秱动，则当 PA + PD取最小值时，△APD中边 AP上的高为(   ) 

解：作点 A关于 BC的对称点 A ' ，连接 A ' D ，交 BC   于点 P  

则 A ' D  =  PA '+ PD  =  PA + PD   A ' D   的长就是 PA + PD   的最小值  S △ APD  = 4 

在直角 △ ABP中，AB  = 4 ，BP  = 1，根据勾股定理，得

 AP =

∴ AP上的高为： 

在九年级下册圆的知识当中也有考到。

Part 6. 圆形  

1 ．已知 ⊙ O 的直径 CD为 4 ， ∠ AOD的度数为 60°，点 B 是AD的中点，在直径 CD 上找一点 P ，使 BP + AP的值最小，并求 BP + AP   的最小值．  

解：在直线 CD 上作一点 P ，使 PA + PB   的值最小作点 A关于 CD 的对称点 A ' ，连接 A ' B ，交 CD 于点 P ，则 A ' B 的长就是 PA + PB 的最小值，连接 OA '，OB ，则∠ A 'OB =90° ，OA ' =OB=4。根据勾股定理，A ' B = 

Part 7. 一次函数 

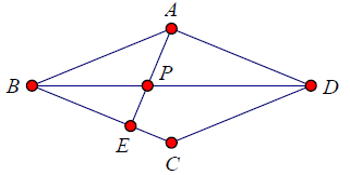
1.一次函数 y = kx + b   的图象与 x 、 y   轴分别交于点 A ( 2 ， 0 )， B ( 0 ， 4 )。 

( 1 )求该函数的解析式；  

( 2 ) O为坐标原点，设 OA . AB   的中点分别为 C . D ， P   为 OB   上一动点，求 PC ＋ PD   的最小值，并求取得最小值时 P点坐标。 

解：(1) 由题意得：0=2 x + b ， 4= b  

  解得   k =-2 ， b =4 ，  

  ∴   y =-2 x +4 

(2) 作点 C   关于 y   轴的对称点 C ' ，连接 C ' D ，交 y   轴于点 P  

则 C ＇ D = C ' P + PD  =  PC + PD  

C ' D   就是 PC + PD   的最小值  

连接 CD ，则 CD =2 ， CC ′=2 

在直角 △ C ' CD   中，根据勾股定理   C ＇ D =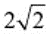 

求直线 C ' D   的解析式，由 C '(-1 ， 0) ， D (1 ， 2) 

∴ 有 0=- k + b ， 2= k + b  

解得   k =1 ， b =1 ，  

∴   y = x +1 

当 x =0  时， y  =1 ，则 P (0 ， 1) 

Part 8. 二次函数  

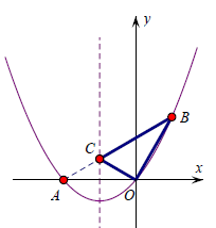
1 ．如图，在直角坐标系中，点 A   的坐标为( -2 ， 0 )，连结 0 A ，将线段 OA 绕原点 O顺时针旋转 120°，得到线段 OB 。

( 1 )求点 B 的坐标；  

( 2 )求经过 A . O 、 B 三点的抛物线的解析式；  

( 3 )在( 2 )中抛物线的对称轴上是否存在点 C ，使 △ BOC   周长最小？若存在求出点 C   坐标；若不存在，请说明理由。

1

通过以上问题的分析，给我们这些启示：

基于对将军饮马问题"的探索,我认为对学生数学学习有两方面的启示:

最短距离问题是初中阶段典型的几何最值问题。平行线、三角形、四边形、圆等几何图形均可作为这个模型的载体，勾股定理、函数等知识也与它联系紧密 ，尤其是结合图形变换后，这类问题对学生分析问题、解决问题的能力要求更高，所以，学生在学的过程中，不能只强调解题技巧，学生要学会剖析问题本职及解题原理。学生找到分层拓展训练，渗透转化、化归、迁移等数学思想，促使学生在积累解题经验的同时提升认知水平。

黄迟：成都市中学数学名师，中学数学竞赛一级教练员，领川外国语学校中学数学竞赛组骨干成员。

END

编   辑：“成都小升初名校指典”兴致语文工作室 

欢迎关注：成都小升初名校指典QQ群：

1群：309483051 

2群：104780329 

  3群：630865554

4群：711176375

  5群：897459042

  6群：254627576

小升初、转学考名校指典语文数学系列教材