三个不等_高中数学竞赛——一道不等式题目的多种证法及讨论

一道不等式题目的多种证法及讨论

我们先来看这样一道不等式问题：

实数

满足

且

. 求证：

均值不等式

注意到当

时，不等式能够取到等号. 已知条件给出了一次对称多项式

的值，所以我们可以根据等号成立条件、利用均值不等式进行如下的配凑：

三式相加，得证.

切线法

这道题目其实也可以用切线法来做（即使没第一眼就看出来，看过上面的解法也很容易就想得到了）.

设

，则

所以，有

，进而可知

的图像在

处的切线方程为

我们尝试证明：

这等价于

上式显然成立.

于是，有

琴生不等式

谈到了切线法，就不得不把“琴生不等式”也搬出来了.

我们还是设

，则

所以

在定义域内下凸，由琴生不等式，可得

更过内容请见微信公众号：数学竞赛的内功心法
部分视频讲解可关注bilibili：清华学长QuDer

进入正题

以上三种方法各有千秋.

一、利用均值不等式做法简洁且更具观赏性，而且即使把问题修改为证明

也可以采用同样的方法.

二、切线法是一种构造局部不等式来完成证明的方法，可以总结为：

对于

，

，

为给定区间，

为常数，求证

这样的不等式，若

可导，当观察得取等条件为

，可以找出

在

处的切线函数

，可尝试证明

若此不等式在区间

内恒成立，则原不等式成立.

值得注意的是，上面提到的

不一定恒成立！有时我们可以通过分类讨论来解决问题（例如：设

，求证：

这道题目就可以用切线法结合分类讨论来证明，证明放在本篇文章最后），有时我们也需要转变思路，更换其他的方法，切线法是一种试探性的尝试，并非万能.

三、用琴生不等式来做这道题，明显有些小题大做了. 也有人认为能用切线法解决的问题肯定都是“上凸”或者“下凸”的，所以都可以用琴生不等式直接证明，但事实并不是这样的！我们看下面这个简单的例子：

，

. 求证：

证明 利用恒等式

我们只需证明

在

处的切线为

，我们可尝试证明

而由均值不等式，我们有

故

式成立.

这里，

既非上凸也非下凸，但是图象恒在直线

的上方，所以可以用切线法，但不能直接用琴生不等式.

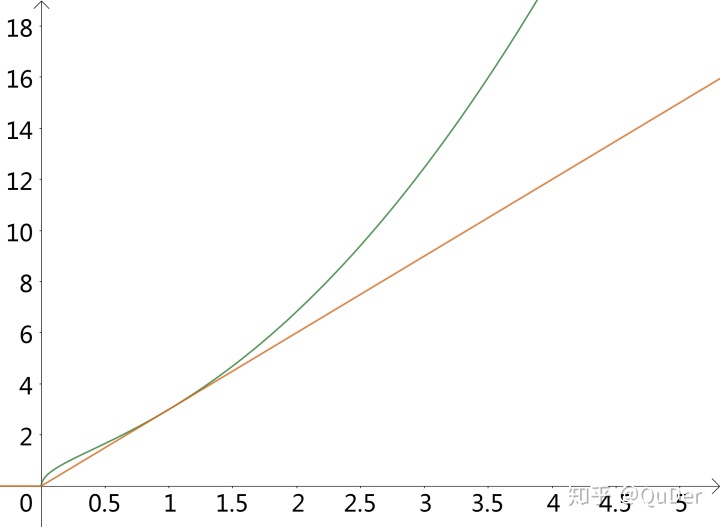
切线法与分类讨论

设

，求证：

证明 观察一下要证的不等式，对称还齐次. 那我们就直接给他来个全套：不妨设

且

. 将三个括号平方后化简，记

，则原不等式等价于

对

求导，可得

. 现在尝试证明：

对上式进行整理，其等价于

至此，我们需要增加条件：

.

由于

，我们需要分如下两种情况讨论：

• 若
  ，当然就证完了；
• 若
  中有大于
  的，则一定是
  ，由于
  ，可得
  ，所以
  ，故

综合以上两种情况，原不等式成立.