深度探索：机器学习中的高斯混合模型（GMM）原理及其应用

最新推荐文章于 2025-02-28 10:14:45 发布

生瓜蛋子

最新推荐文章于 2025-02-28 10:14:45 发布

阅读量1.1w

点赞数 45

分类专栏：机器学习文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/qq_51320133/article/details/137955398

版权

机器学习专栏收录该内容

154 篇文章

订阅专栏

1. 引言与背景

在现代机器学习领域，数据分布的复杂性和多样性要求我们采用灵活且强大的模型来捕捉潜在的规律和结构。高斯混合模型（Gaussian Mixture Model, GMM）作为一种无监督的概率模型，以其对多元数据分布的强大建模能力而备受青睐。它假设数据是由多个高斯分布（正态分布）叠加而成，每个高斯分布代表数据空间中的一个潜在类别或簇。这种混合模型能够刻画非线性、非凸的数据分布，广泛应用于聚类分析、异常检测、密度估计、语音识别、图像分割等诸多场景。本文旨在全面探讨高斯混合模型的理论基础、算法原理、实现细节、优缺点，并通过案例应用和与其他算法的对比，展现其在实际问题中的强大适应性和未来研究展望。

2. 高斯混合模型定理

高斯混合模型的核心定理是其概率密度函数（PDF），表达为：

其中：

x 是待建模的多维数据点。
K 是混合成分的数量，即潜在高斯簇的个数。
$\pi _{k}$ 是第 k 个高斯分布的混合权重，满足 $\sum_{K-1}^{K}\pi _{k}= 1$ 和 $\pi _{k}> 0$ 。
$\mathbb{N}\left ( X|\mu _{k},\sum _{k} \right )$ 表示第 k 个高斯分布，其均值为 $\mu _{k}$ ，协方差矩阵为 $\sum _{k}$ 。

高斯混合模型的参数集 θ 包括所有混合权重、均值向量和协方差矩阵。通过对这些参数的学习，GMM能够对数据分布进行灵活而精细的建模。

3. 算法原理

高斯混合模型的学习通常采用期望最大化（Expectation-Maximization, EM）算法，这是一种迭代优化算法，旨在最大化观测数据的对数似然函数。EM算法分为两步：

E步骤（期望步）：对于给定的参数 θ，计算每个数据点 $x_{i}$ 属于每个高斯分量 k 的后验概率（责任权重）：

M步骤（最大化步）：根据E步骤得到的责任权重，更新模型参数：

更新混合权重：
更新均值向量：

其中 $N_{k}= \sum_{i-1}^{N}r_{ik}$ 是分配给第 k 个分量的“有效”样本数。
更新协方差矩阵：

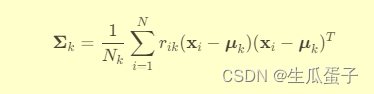
重复E步和M步直至收敛（如参数变化小于某个阈值或达到最大迭代次数），得到最优参数 $\theta ^{*}$ 。

4. 算法实现

在Python中实现高斯混合模型（Gaussian Mixture Model, GMM）通常可以借助于成熟的机器学习库，如scikit-learn。下面是一个详细的代码讲解，包括数据准备、模型训练、模型参数解释以及对新数据进行预测（聚类）和密度估计：

1. 数据准备

首先，我们需要准备一个二维数据集，这里以随机生成的示例数据为例：

Python

import numpy as np

# 生成模拟数据，假设包含三个簇（对应高斯混合模型的三个分量）
np.random.seed(42)  # 设置随机种子以确保结果可复现
n_samples = ½000
n_clusters = 3
centers = [[1, 1], [-1, -1], [1, -1]]
covariances = [np.eye(2), np.eye(2), np.eye(2)]

X = np.zeros((n_samples, 2))
for i in range(n_clusters):
    n_samples_i = int(n_samples / n_clusters)
    X[i * n_samples_i:(i + 1) * n_samples_i, :] = np.random.multivariate_normal(
        centers[i], covariances[i], size=n_samples_i
    )

print("Sample data shape:", X.shape)

这段代码生成了一个包含5000个样本的二维数据集（每个样本有两个特征），数据集模拟了三个互相分离的簇，每个簇由一个二维高斯分布生成。

2. 模型训练

接下来，我们使用scikit-learn的GaussianMixture类来训练高斯混合模型：

Python

from sklearn.mixture import GaussianMixture

# 初始化GMM模型，设定混合分量数量K=3
gmm = GaussianMixture(n_components=n_clusters, covariance_type='full')

# 训练模型
gmm.fit(X)

# 输出模型参数
print("Weights (mixing coefficients):", gmm.weights_)
print("Means of each component:", gmm.means_)
print("Covariances of each component:", gmm.covariances_)

n_components参数指定了混合模型中的高斯分量数量，这里设置为3，与数据生成时的簇数量一致。
covariance_type参数决定了协方差矩阵的形式，取值可为'full'（全协方差矩阵）、'tied'（所有分量共享同一协方差矩阵）、'diag'（对角协方差矩阵）或'spherical'（球形协方差，即所有维度具有相同方差）。这里使用全协方差矩阵。

3. 对新数据进行预测（聚类）

有了训练好的模型，我们可以对新的数据点进行聚类预测：

Python

# 假设有一些新的二维数据点需要进行聚类
new_data = np.array([[0.⅛, 0.⅛], [-0.⅛, -0.⅛], [0.⅛, -0.⅛]])

# 使用模型的predict方法进行聚类预测
labels = gmm.predict(new_data)

print("Cluster labels for new data points:", labels)

predict方法返回新数据点所属簇（即对应高斯分量的索引）的标签。

4. 密度估计

除了聚类，GMM还可以用于估计数据点的生成概率（即数据点在模型下的密度），这对于异常检测等任务非常有用：

Python

# 计算新数据点的密度（log-likelihood）
densities = gmm.score_samples(new_data)

print("Log-likelihood densities for new data points:", densities)

score_samples方法返回每个数据点的对数似然得分，值越大表示数据点在当前模型下越“正常”。

综上所述，通过使用scikit-learn库中的GaussianMixture类，我们可以轻松地在Python中实现高斯混合模型的训练、聚类预测以及密度估计。这样的实现不仅简洁高效，而且得益于scikit-learn的良好封装，使得模型的使用和参数调整变得十分便捷。

5. 优缺点分析

优点：

灵活性：通过调整混合分量数量，GMM能够适应不同复杂程度的数据分布。
概率解释：每个数据点被赋予属于各高斯分量的概率，提供清晰的聚类解释。
密度估计：可用于估计数据点的生成概率，适用于异常检测等任务。
自然处理连续变量：适用于具有连续特征的数据集。

缺点：

参数选择：混合分量数量 �K 的选取对模型性能影响显著，但往往需要通过交叉验证等方法确定。
局部最优：EM算法易陷入局部最优，特别是在初始值选择不佳或数据分布复杂时。
对异常值敏感：异常值可能导致协方差矩阵病态，影响模型稳定性。

6. 案例应用

语音识别：GMM常用于语音信号的特征建模，每个发音单元（如音素）对应一个GMM，通过最大似然判决进行识别。

图像分割：GMM可用于像素级的图像聚类，每个分量对应图像的一个区域，实现自动分割。

金融风险评估：在信用评分或市场风险分析中，GMM可用于识别不同风险等级的客户群体或资产组合。

7. 对比与其他算法

与K-means的对比：

概率框架与硬/软聚类：
- GMM：基于概率生成模型，认为数据是由多个高斯分布（即混合成分）按一定比例混合生成的。每个数据点不仅被分配到某个聚类，还具有相应的隶属度（或称软聚类），即属于各个高斯分布的概率。这种软聚类特性允许数据点部分地属于多个聚类，提供了更丰富的信息和更平滑的边界。
- K-means：基于距离的划分方法，每个数据点严格地被分配到最近的聚类中心所在的簇，形成硬边界。数据点仅属于一个簇，没有隶属度的概念。
对数据分布的假设：
- GMM：假设数据服从多元高斯分布，能够适应各种复杂的、非线性的、非凸的数据分布，特别适合处理具有椭圆状分布结构的簇。
- K-means：假定簇是凸的且各簇大小差异不大，对于形状规则、分布均匀的数据集表现良好。当数据集中的簇形状不规则、大小差异显著或存在非球形分布时，K-means的性能可能下降。
聚类数量的确定：
- GMM：需要事先指定混合成分的数量（即聚类数量），虽然可以通过交叉验证、BIC/AIC准则等方法选择最优的K值，但过程相对复杂。
- K-means：同样需要预先设定K值，但其收敛速度较快，对大规模数据集的处理效率较高。
计算复杂性与收敛性：
- GMM：通常采用期望最大化（EM）算法进行迭代优化，计算复杂度较高，尤其是当协方差矩阵为全协方差时。不过，GMM通常收敛较稳定，即使初始状态不佳，也能找到局部最优解。
- K-means：算法简单，计算效率高，容易并行化处理，收敛速度快。然而，其收敛性对初始聚类中心敏感，可能陷入局部最优，且对于大规模数据集或高维数据可能存在“空洞”问题。

与DBSCAN的对比：

聚类原理与假设：
- GMM：基于概率分布建模，对数据集的全局结构进行描述，适合处理数据点分布存在潜在高斯分布的情况。
- DBSCAN：基于密度聚类，不需要对数据分布做出特定假设。它通过定义邻域半径（ε）和最小邻域点数（MinPts）来识别核心对象和边界对象，自动发现任意形状的簇，尤其擅长处理噪声、离群点和复杂形状的聚类。
聚类数量的确定与对噪声的处理：
- GMM：需要预设聚类数量，对噪声处理相对较弱，噪声点可能会被错误地纳入某个高斯分布中。
- DBSCAN：无需指定聚类数量，能自动识别噪声点（标记为“噪声”或“边界”），对噪声和离群点具有较强的鲁棒性，且能够发现任意大小和形状的簇。
对数据集规模和维度的适应性：
- GMM：随着数据集规模增大或维度增加，计算复杂度显著上升，对内存和计算资源的需求较高。
- DBSCAN：尽管计算复杂度也随数据集规模和维度增长，但由于其局部性特点，对大规模数据集的处理相对较好，尤其是在较低维度空间。然而，对于高维数据，选择合适的ε和MinPts参数可能较为困难。
概率解释与密度估计：
- GMM：提供每个数据点属于各个高斯分布的概率（隶属度），能够进行密度估计，对数据生成机制提供概率解释。
- DBSCAN：不提供概率解释或密度估计，聚类结果仅表现为簇的划分。

总结而言，选择哪种聚类算法取决于具体的应用场景和数据特性。如果数据集规模较小、分布近似高斯且对概率解释和密度估计有需求，GMM可能是更好的选择。对于大规模、高维或具有复杂形状和噪声的数据集，DBSCAN可能更为合适。而K-means适用于数据分布均匀、形状规则、簇大小相近且对计算效率要求较高的情况。

8. 结论与展望

高斯混合模型凭借其强大的概率建模能力和广泛应用前景，在机器学习领域占据重要地位。尽管存在参数选择难题和局部最优风险，但通过结合先验知识、使用合适的初始化策略、引入贝叶斯框架或与其他算法（如深度学习）融合，可以有效提升GMM的性能和泛化能力。随着计算资源的增长和算法研究的深入，高斯混合模型及其变种有望在更大规模、更高维度、更复杂结构的数据分析任务中发挥关键作用。同时，对模型选择、优化算法和混合模型族的理论研究也将持续推动该领域的进步。