Karp-Rabin算法（）不完备定理

哥德尔不完全性定理

哥德尔的不完备性定理是数学逻辑的两个定理，它们证明了每个能够建模基本算术的正式公里系统的固有局限性。这些结果由KurtGödel于1931年出版，在数学逻辑和数学哲学都很重要。这些定理被广泛地，但不是普遍地解释为表明希尔伯特为所有数学找到完整一致的公里集的程序是不可能的。

第一定理

第一个不完备性定理指出，没有一致的公理系统，其定理可以通过有效的程序（即算法）列出，能够证明关于自然数的算术的所有真理。对于任何这样一致的正式系统，总会有关于自然数的陈述是真实的，但这在系统内是不可证实的。

任意一个包含一阶谓词逻辑与初等数论的形式系统，都存在一个命题，它在这个系统中既不能被证明为真，也不能被证明为否。

第二定理

如果系统S含有初等数论，当S无矛盾时，它的无矛盾性不可能在S内证明。第二个不完备性定理，即第一个不完备性定理，表明系统无法证明其自身的一致性。

采用对角线论证，哥德尔的不完备性定理是关于正式系统局限性的几个密切相关的定理中的第一个。他们之后是关于真理的正式不确定性的塔斯基不可定理论，教会证明希尔伯特的Entscheidungsproblem无法解决，以及图灵的定理，即没有算法来解决停止问题。

 

凡物皆数

Gödel numbering：逻辑系统的符号、表达式、公式、命题、定理、公理等均可以不同的自然数标识。

在数学逻辑中，哥德尔编号是一种函数，它为每个符号和一些形式语言的格式良好的公式分配一个唯一的自然数，称为哥德尔数。这个概念被KurtGödel用来证明他的不完备性定理。

素数序列： P(k)= 第k个素数 （2，3，5，7，11 .... ）

素数虽然是无限的，但是同时也是可数的，因此我们可以用P(k)来指代第k个素数。

每个有限维的自然数向量，唯一对应于一个自然数

比如 我们来考察这样一个由整数构成的8维向量，它的各个分量依次为3 1 4 1 5 9 2 6，我们现在来找出它所对应的那个自然数。

既然是8维 所以我们要首先要搬出前8个素数，也就是2 3 5 7 11 13 17 19，这8个素数将分别与向量的8个分量一一配对

第1个分量为3，所以我们相应地将它转换为第1个素数 2的3+1也就是4次方

第2个分量为1，所以我们也将它转化为第2个素数 3的1+1也就是2次方

第3个分量是4，所以我们也将它转化为第3个素数 5的4+1也就是5次方

以下依次类推

我们可以得到第4个素数的1+1次方，第5个素数的5+1次方，第6个素数的9+1次方，第7个素数的2+1次方，以及最后 第8个素数的6+1次方，显然 这8个因子的乘积依然应该是一个自然数。也就是说，如此 我们的确可以将任何一个向量 转化为一个自然数。

而这种转换方法还具有一个更为精妙、更为神奇的特征，根据如此得出的一个自然数，我们还可以反过来忠实地还原此前的向量。

设计算出的自然数为 U，向量维度n，前n个素数记为{xi}，对应次幂为{ai}

思路：用xi除U，能除出几个，ai值就为几,当前xi除不出来，换下一个

初始化 i=0 ai=0
while(U>1)
  if U%xi ==0   ai++;U/=xi;
  else i++

散列表（哈希表）亦可视作这一思想的产物。从这一角度来看，散列之所以可实现极高的效率，正在于它突破了通常对关键码的狭义理解——允许操作对象不必支持大小比较——从而在一般类型的对象（词条）与自然数（散列地址）之间，建立起直接的联系。 

 

串亦为数

既然万事万物的本源都对应与自然数，那么串也自然应该对应于数。接下来我们就来看看，这句话如何兑现。

首先来考虑一种我们最为熟悉的串，也就是由10进制数字所构成的串。比如 由阿拉伯数字所构成的这样一个串，如果我要说这个串是一个自然数，我想你不会有任何异议的。没错，这正是我们最常用的技术方法。

那么 一般的串呢？你应该还记得我们的约定——组成字符串的每一个字符都来自于事先约定的某个字母表。而在这里，字母表的规模又是至关重要的。

如果将它记作d，那么字母表中的所有字符也就可以按照任何一种次序 与0与d-1之间的整数一一对应了。

于是 基于这个字母表所建立起来的任何一个字符串都可以视作为一个d进制的自然数。

不妨考察以26个大写英文字母所构成的字符集，于是 由大写字母所构成的任何一个英文单词也必然对应于某个26进制的自然数。比如在单词CAT中，C对应的编号为2，A对应于0，而T对应于19。如果你关心这个数字的具体数值，不妨借鉴一下我们在第4章所给出的进制转换算法。不过，这个方法还存在一点小小的瑕疵，好在修补这个瑕疵并不困难，这一任务不妨由你在课后独立地来完成。

既然每一个串都可以对应于一个自然数，那么接下来很自然地，一个模式串在某个主串中能够出现，仅当这个子串在数值上与模式串相等。请注意，经过这样的视角转换，我们已经在无形中将串与串的比对转化为了整数与整数的比对。也就是说串与串之间的比对将有望在常数的时间内完成。果真如此，以上也就自然给出了一个串匹配的算法。

 

数位溢出/散列压缩

我们将每一个串所对应的自然数称作为它的指纹（fingerprint），因为这个数相对于串 就像指纹相对于人一样，可以用来甄别其身份。然而我们注意到，这样一个自然数是以字符集的规模作为进制的，因此字符集只要不是很小，这类指纹的数值就会变得很大。

这不能不说是个坏消息，比如 我们知道对于ASCII字符集来说，它的规模为128，对于这类字符，即便模式串的长度不是特别地长，它对应的指纹也会长得令我们吃不消。

我们可以来做一个快速的封底估算：128是2的7次方，因此即便是长度为10的模式串，它所对应的指纹也至少需要70个比特方能表示。这就意味着，即便在64位的计算平台上，长度不小于10的字符串，将无法直接表示。而更糟糕的是 我们因此而遇到的麻烦还不止这些。实际上 在整数的字宽已经不能继续视作为常数之后，整数之间的运算，也不能继续保证可在常数时间内完成。尽管RAM模型曾经的确作过这样一个不切实际的假设，实际上 就渐进复杂度的意义而言，此时 每次指纹比对所需要的时间，将仍然线性正比于串的长度。也就是说 我们的计算效率将重新退化到蛮力算法的水准。

既然以上的根源在于数位溢出，那么我们很自然地就会应该想到通过压缩来解决它。没错，将一个硕大的取值空间压缩到一个可存储、可计算的 更小的空间。从方法论上讲，这不正是散列吗。没错 我们需要对指纹来做散列压缩，具体地 我们将借助合适的散列函数，将字符串的指纹压缩到存储器可支持的范围。

 

散列冲突

注意：hash()的值相等，并非匹配的充分条件（好在是必要条件）。

因此，通过hash()筛选之后，还需严格的对比，方可最终确定是否匹配。

来看这样一个实例，依然是刚才我们已经熟知的那个文本串，只不过这里将模式串替换为1 8 2 8 4。首先确认 模式串的指纹为48，以下 我们依然是去逐个尝试每一个对齐位置。在第一个对齐位置 我们得到的是指纹22，既然它与目标的48不等，我们也可自然地将这一对齐位置排除掉。接下来的第2个对齐位置，所对应的局部子串是7 1 8 2 8。很显然 它并不是我们要找的模式串。然而很不幸，它所对应的指纹却是48，与模式串的指纹一模一样。当然 这也没有什么奇怪的，两个不同的元素在经过散列变化之后，有可能会被映射到同一个散列码，这种现象正是我们所谓的冲突。好在我们沿用了散列表的策略。

我们在这种情况下还会对这两个字符串作逐位的比对，以最终确定它的确是匹配。当然 经过这样的严格比对之后，我们也的确可以排除掉这个对齐位置。事实上 这个算法会如此不断地运行下去，直到最终抵达真正的匹配串 也就是1 8 2 8 4。当然 我们的算法在此 也不会遗漏掉这次匹配，因为显然 这个局部子串所对应的散列码，也应该是48。

 

指纹更新

为了计算出文本串中每一个子串所对应的指纹，我们所需要花费的时间，似乎都需线性正比于子串的长度。当然，也就是模式串的长度，如果考虑到有多达O(n)个这样的潜在子串，那么你或许会沮丧地发现，最终的整体时间复杂度又再一次回到了O(n*m)。难道我们此前的心血都是白费的吗？这也是我们在最后这一小步中所要解决的一个关键问题。

我们思考的方向和目标是将每一指纹的计算成本从O(m)降低到常数。

如果你还没有想出有效的方法，不妨首先温习一下此前的进制转换算法。或许你能从中得到一些启示。

没错，在那个算法中我们很好地利用了相邻数位之间的相关性。其实在这里 也存在着类似的相关性。在文本串中，任何两个相邻子串之间都存在着紧密的相关性。具体来说 二者的指纹之间存在着相关性。而这两个指纹的计算过程及结果之间也存在着紧密的相关性。

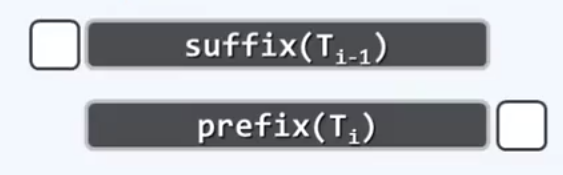
从这幅图中可以看出，相邻的子串几乎一样。二者唯一的区别只在于前者的首字符以及后者的末字符。也就是说，前一子串删除首字符之后的后缀，与后一字串删除末字符之后的前缀完全相同。

利用这种相关性，可以根据前一字串的指纹，在常数时间内得到后一字串的指纹。也就是说，整个算法过程中消耗于子串指纹计算的时间，平均每次仅为O(1)。

//字串指纹快速更新算法
void updateHash(HashCode& hashT,char& T,size_t m,size_t k,hashCode Dm){
    hashT=( hashT - DIGIT(T,k-1) * Dm ) % M ; //在前一指纹基础上，去除首位T[k-1]
    hashT=( hashT * R + DIGIT(T,k+m-1)) % M ; //添加末位T[k+m-1]
    if(0>hashT)
        hashT += M ;                          //确保散列码落在合法区间内
}

这里，前一子串最高位对指纹的贡献量应为p[0] x 。只要注意到其中始终不变，即可考虑如下面代码所示，通过预处理提前计算出对应的模余量。

为此尽管可以采用快速幂算法power2()，但考虑到此处仅需调用一次，同时兼顾算法的简洁性，故不妨直接以蛮力累乘的形式实现。

HashCode prepareDm(size_t m){    //预处理：计算R^(m-1)%M (仅需调用一次，不必优化)
    HashCode Dm = 1 ;
    for(size_t i=1;i<m;i++)
        Dm = ( R * Dm ) % M;     //直接累乘m-1次，并取模
    return Dm;
}

 

 

 

 

参考文献：

https://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems

https://en.wikipedia.org/wiki/G%C3%B6del_numbering

邓俊辉《数据结构/c++语言版》