优化算法 | 手把手教你改进鲸鱼优化算法（附8个算法创新点）

今天为各位讲解改进鲸鱼优化算法（Improved Whale Optimization Algorithm，IWOA），近两年关于鲸鱼优化算法（WOA）的论文比较多，对WOA算法改进的研究也是层出不穷，今天这篇推文主要针对无约束连续优化问题，提出应用WOA算法求解的改进思路。如果想了解标准WOA算法，可以在优化算法 | 鲸鱼优化算法这篇推文中进行学习，当然，我们也会在本篇推文中对标准WOA算法做一个简短的回顾。

---

1.标准WOA算法

WOA是模仿自然界中鲸鱼捕食行为的新型群体智能优化算法，而鲸鱼的捕食行为主要分为3类：1）包围猎物；2）发泡网攻击；3）搜索捕食。接下来分别对上述3类捕食行为用数学公式进行表示。

1.1 包围猎物

假设在$d$维空间中，当前最佳鲸鱼个体的$X^{\ast }$位置为$\left(X_1^{\ast },X_2^{\ast },\cdots ,X_d^{\ast }\right)$，鲸鱼个体的位置$X^j$为$\left(X_1^j,X_2^j,\cdots ,X_d^j\right)$。则鲸鱼个体$X^j$在最佳鲸鱼个体$X^{\ast }$的影响下的下一个位置的计算公式如下$X^{j_{-}new}\left(X_1^{j_{-}new},X_2^{j_{-}new},\cdots ,X_d^{j_{-}new}\right)$：
$$\begin{array}{c}{X}_k^{j_{-}new}=X_k^{\ast }-A_1\cdot D_k(1)\\ D_k=\left|C_1\cdot X_k^{\ast }-X_k^j\right|(2)\\ C_1=2r_2(3)\\ A_1=2a\cdot r_1-a(4)\end{array}$$
其中$X_k^{j_{-}new}$表示空间坐标的$X^{j_{-}new}$第个分$k$量。计算公$D_k$式中的表示求绝$||$对值的含义。是$a$随着迭代次数的增加，从2至0线性递减。$r_1$和$r_2$中都是0至1之间的随机数。

1.2 发泡网攻击

发泡网攻击是座头鲸特有的吐气泡捕食行为，为了模拟这种捕食行为，现分别设计两种数学模型表达上述捕食行为。假设在$d$维空间中，当前最佳鲸鱼个体$X^{\ast }$的位置为$\left(X_1^{\ast },X_2^{\ast },\cdots ,X_d^{\ast }\right)$，鲸鱼个体$X^j$的位置为$\left(X_1^j,X_2^j,\cdots ,X_d^j\right)$。

a）收缩包围。这种捕食行为与上述包围猎物行为的数学模型几乎完全相同，区别之处在于$A_1$的取值范围。因为收缩包围的含义为将当前位置的鲸鱼个体向当前最佳位置的鲸鱼个体靠近，所以$A_1$的取值范围由原来的$[-a,a]$调整为$[-1,1]$，其它公式保持不变。

b）螺旋式位置更新。当前鲸鱼个体以螺旋式的方式向当前最佳鲸鱼个体靠近。
$$\begin{array}{c}{X}_k^{j_{-}\text{new }}=X_k^{\ast }+D_k\cdot e^{bl}\cdot \cos (2\pi l)(5)\\ D_k=\left|X_k^{\ast }-X_k^j\right|(6)\end{array}$$
其中$b$为对数螺旋形状常数，$l$为$-1\sim 1$之间的随机数。

座头鲸在围捕猎物时，不仅收缩包围圈，而且以螺旋形式向猎物游走，因此各以50%的概率选择收缩包围圈，或是选择以螺旋形式向猎物游走，数学模型如下：
$$X_k^{j_{-}\text{new }}=\{\begin{array}{cc}{X}_k^{\ast }-A_1\cdot D_k& p<0.5\\ X_k^{\ast }+D_k\cdot e^{bl}\cdot \cos (2\pi l)& p\ge 0.5\end{array}(7)$$

1.3 搜索捕食

在收缩包围的捕食行为的数学模型中$A_1$的取值范围限制为$[-1,1]$，但是当$A_1$的取值不在$[-1,1]$时，这时当前鲸鱼个体可能不会向当前最佳鲸鱼个体靠近，而是从当前鲸鱼群体中随机选择一条鲸鱼个体靠近，这就是搜索捕食的思想。

搜索捕食虽然可能会使当前鲸鱼个体偏离目标猎物，但是会增强鲸鱼群体的全局搜索能力。假设在$d$维空间中，当前鲸鱼群体中随机一个鲸鱼个体$X^{rand}$的位置为$\left(X_1^{\text{rand }},X_2^{\text{rand }},\cdots ,X_d^{\text{rand }}\right)$，鲸鱼个体$X^j$的位置为$\left(X_1^j,X_2^j,\cdots ,X_d^j\right)$，则搜索捕食行为的数学模型如下：
$$\begin{array}{c}{X}_k^{j_{-}new}=X_k^{\text{rand }}-A_1\cdot D_k(8)\\ D_k=\left|C_1\cdot X_k^{\text{rand }}-X_k^j\right|(9)\\ C_1=2r_2(10)(10)\\ A_1=2a\cdot r_1-a(11)\end{array}$$

---

2.改进WOA算法创新点

2.1 自适应参数

2.1.1 启发式概率$p_1$

为了平衡标准WOA全局搜索和局部搜索能力，启发式概率$p_1$计算公式如下：
$$p_1=\{\begin{array}{ll}0.7& t<0.5\ast \text{ maxIter }\\ 0.4& t\ge 0.5\ast \text{ maxIter }\end{array}(12)$$
其中$t$为当前迭代次数，$maxIter$为最大迭代次数。

2.1.2 自适应惯性权重$\omega$

在迭代过程中，将鲸鱼个体的适应度$ f(i)$按升序排序，然后分成两半分别求平均适应度$ f_{avg1}$和$ f_{avg2}$，其中$f_{avg1}<f_{avg2}$，将当前鲸鱼个体的适应度分与$ f_{avg1}$和$ f_{avg2}$比较，将惯性权重分类如下：

（1）$ f(i)<f_{avg2}$

$\omega$取值为$(0.8,1.2)$之间的随机数。

（2）$f(i)\ge f_{avg2}$

$\omega$以50%的概率取为$(0.3,0.6)$或$(1.3,1.6)$之间的随机数。

（3）$ f_{avg1}<f(i)<f_{avg2}$

$\omega$取值为1。

2.1.3 线性控制参数$l$

$$\begin{array}{l}l=\left(a_2-1\right)\times \text{ rand }+1-2\times \frac{t}{\text{ maxIter }}(13)\\ a_2=-1-\frac{t}{\text{ maxIter }}(14)\end{array}$$

2.2 全局搜索方法

2.2.1 $\text{ Leˊvy }$飞行策略

采用$\text{ Leˊvy }$飞行策略可以增强算法的全局搜索能力。鲸鱼个体$X^i$采用$\text{ Leˊvy }$飞行策略更新位置的公式如下：
$$X_{\text{new }}^i=X^i+A_1\times 0.01\times \text{ step }\oplus \left(X^i-C_1\times X^{\text{rand }}\right)(15)$$

其中$X_{\text{new }}^i$为鲸鱼个体$X^i$更新后的位置，$A_1$和$C_1$的含义同公式（1）中的$A_1$和$C_1$，$\oplus$表示点乘，$X^{\text{rand }}$表示当前种群中随机选择的鲸鱼个体，$step$表示随机步长，由Mantegna方法产生，公式如下。
$$\mathrm{step}=\frac{u}{|v{|}^{1/\beta }}(16)$$

其中$u\left(u_1,u_2,\cdots ,u_d\right)$和$v\left(v_1,v_2,\cdots ,v_d\right)$为$d$维空间向量，且有$\beta =1.5$，$u$和v$的每个分量均服从如下正太分布。
$$\begin{array}{r}u\sim N\left(0,{\sigma }_u^2\right),v\sim N\left(0,{\sigma }_v^2\right)(17)\\ {\sigma }_u\sim {\left(\frac{\Gamma (1+\beta )\cdot \sin \left(\pi \cdot \frac{\beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\cdot \beta \cdot 2^{\frac{\beta -1}{2}}}\right)}^{\frac{1}{\beta }},{\sigma }_v=1(18)\end{array}$$

2.2.2 初级知识获取-共享算法

将鲸鱼个体的适应度按升序排序，排序结果如下：
$$X^{\text{best }},\cdots ,X^{i-1},X^i,X^{i+1},\cdots ,X^{\text{worst }}$$
初级知识获取-共享算法更新个体方法如下：
$$X_{\text{new }}^i=\{\begin{array}{ll}{X}^i+k_f\times \left[\left(X^{i-1}-X^{i+1}\right)+\left(X^r-X^i\right)\right]& f\left(X^i\right)>f\left(X^r\right)\\ X^i+k_f\times \left[\left(X^{i-1}-X^{i+1}\right)+\left(X^i-X^r\right)\right]& f\left(X^i\right)\le f\left(X^r\right)\end{array}(19)$$
其中$X^i$为待更新个体，$X_{\text{new }}^i$为更新后的个体，$X^r$为随机选择的个体，$k_f$为知识因素参数，取值为0.5。

2.2.3 模拟退火策略

在更新中种群中的个体时，以一定概率接受劣质个体。概率计算公式如下：
$$P=e^{-\frac{\left(f\left(X^{j_{-}new}\right)-f\left(X^j\right)\right)/f\left(X^j\right)}{T}}(20)$$
其中$T$为当前迭代次数时的温度。

2.3 局部搜索方法

2.3.1 修正螺旋位置更新方法

将鲸鱼个体的适应度按升序排序，排序结果为：
$$X^1,\cdots ,X^{i-1},X^i,X^{i+1},\cdots ,X^{\text{popSize }}$$
根据适应度值将鲸鱼个体划分为3类：最佳个体类、中等个体类、最差个体类，且这3类集合中的鲸鱼个体数目分为$0.05\ast popSize$、$0.9\ast popSize$和$0.05\ast popSize$。最佳个体类、中等个体类和最差个体类中的鲸鱼个体分别用$X^{p_{-}best}$、$X^m$和$X^{p_{-}worst}$表示。
$$\begin{array}{l}{X}_k^{j+1}=X_k^{p_{-}\text{best }}+D_k\cdot e^{bl}\cdot \cos (2\pi l)(21)\\ D_k=X_k^{p_{-}\text{best }}-X_k^{p_{-}\text{worst }}+\left|X_k^m-X_k^j\right|(22)\end{array}$$

2.3.2 二次插值法

采用二次差值法对个体$X^i$的更新公式如下：
$$X_d^i=0.5\times \frac{\left[{\left(X_d^i\right)}^2-{\left(X_d^r\right)}^2\right]\times f\left(X^{\ast }\right)+\left[{\left(X_d^r\right)}^2-{\left(X_d^{\ast }\right)}^2\right]\times f\left(X^i\right)+\left[{\left(X_d^{\ast }\right)}^2-{\left(X_d^i\right)}^2\right]\times f\left(X^r\right)}{\left(X_d^i-X_d^r\right)\times f\left(X^{\ast }\right)+\left(X_d^r-X_d^{\ast }\right)\times f\left(X^i\right)+\left(X_d^{\ast }-X_d^i\right)\times f\left(X^r\right)}(23)$$
其中$X^r$为当前种群中随机选择的个体，$X^{\ast }$为当前全局最佳个体。

---

3.改进WOA算法流程图

---

4.改进WOA算法实例验证

在介绍IWOA算法前，先展示一下IWOA求解以下无约束连续优化问题的性能。当将变量个数为10时，即$D=10$时，变量下界设为-100，变量上界设为100，种群规模设为200，迭代次数设为1000，各个测试函数的求解结果如下：

（1）Bent Cigar Function
$$f_1(\mathbf{x})=x_1^2+10^6\sum _{i=2}^D{x}_i^2$$
求解过程如下图所示：

最优值接近0，最优解位置如下所示：

（2）Rastrigin’s Function
$$f_2(x)=\sum _{i=1}^D\left(x_i^2-10\cos \left(2\pi x_i\right)+10\right)$$
求解过程如下图所示：

最优值接近0，最优解位置如下所示：

（3）High Conditioned Elliptic Function
$$f_3(x)=\sum _{i=1}^D{\left(10^6\right)}^{\frac{i-1}{D-1}}{x}_i^2$$
求解过程如下图所示：

最优值接近0，最优解位置如下所示：

（4）HGBat Function
$$f_4(\mathbf{x})={\left|{\left(\sum _{i=1}^D{x}_i^2\right)}^2-{\left(\sum _{i=1}^D{x}_i\right)}^2\right|}^{1/2}+\left(0.5\sum _{i=1}^D{x}_i^2+\sum _{i=1}^D{x}_i\right)/D+0.5$$
求解过程如下图所示：

最优值接近0.5，最优解位置如下所示：

（5）Rosenbrock’s Function
$$f_5(\mathbf{x})=\sum _{i=1}^{D-1}\left(100{\left(x_i^2-x_{i+1}\right)}^2+{\left(x_i-1\right)}^2\right)$$
求解过程如下图所示：

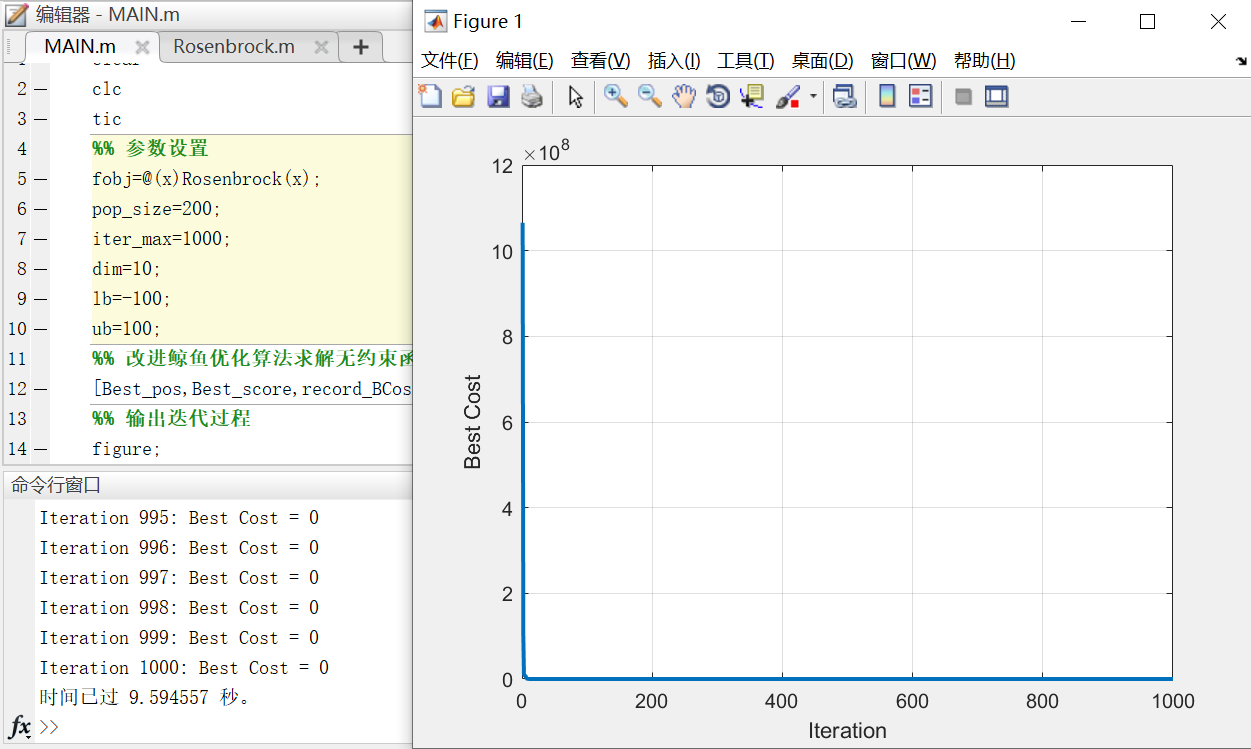
最优值为0，最优解位置如下所示：

（6）Griewank’s Function
$$f_6(\mathbf{x})=\sum _{i=1}^D\frac{x_i^2}{4000}-\prod _{i=1}^D\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$$
求解过程如下图所示：

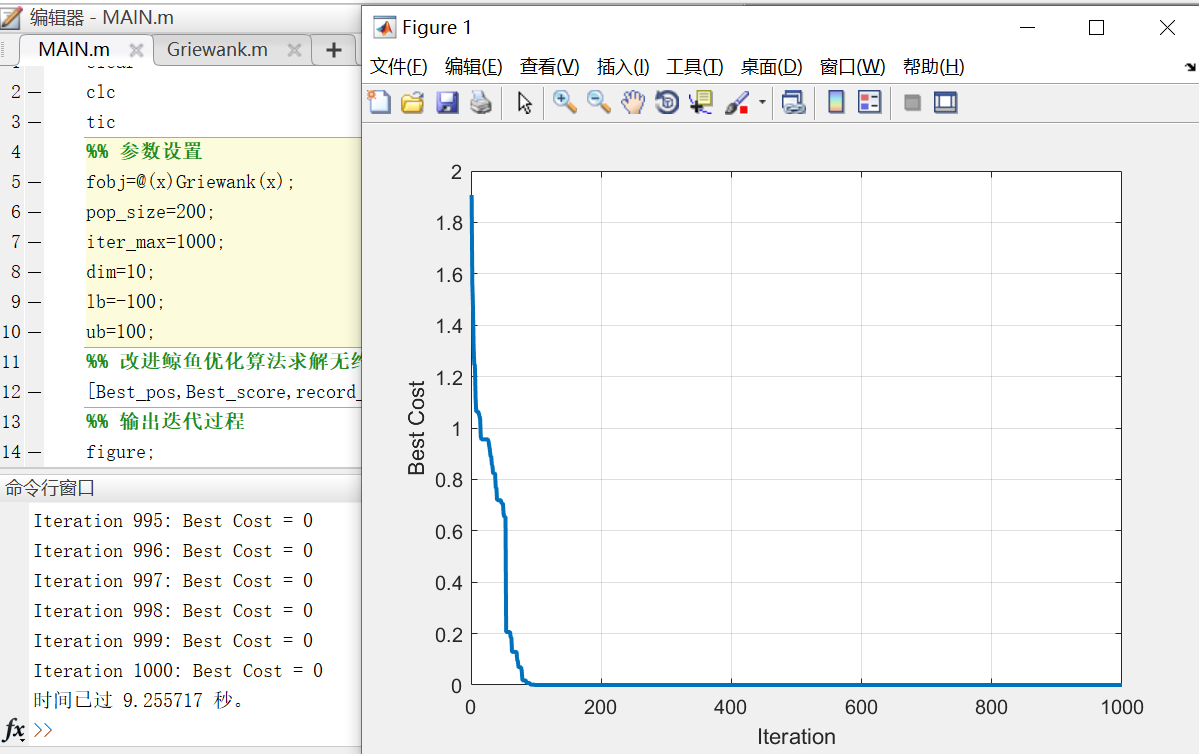
最优值接近0，最优解位置如下所示：

（7）Ackley’s Function
$$f_7(\mathbf{x})=-20\exp \left(-0.2\sqrt{\frac{1}{D}\sum _{i=1}^D{x}_i^2}\right)-\exp \left(\frac{1}{D}\sum _{i=1}^D\cos \left(2\pi x_i\right)\right)+20+\mathrm{e}$$
求解过程如下图所示：

最优值接近0，最优解位置如下所示：

（8）Happycat Function
$$f_8(\mathbf{x})={\left|\sum _{i=1}^D{x}_i^2-D\right|}^{1/4}+\left(0.5\sum _{i=1}^D{x}_i^2+\sum _{i=1}^D{x}_i\right)/D+0.5$$
求解过程如下图所示：

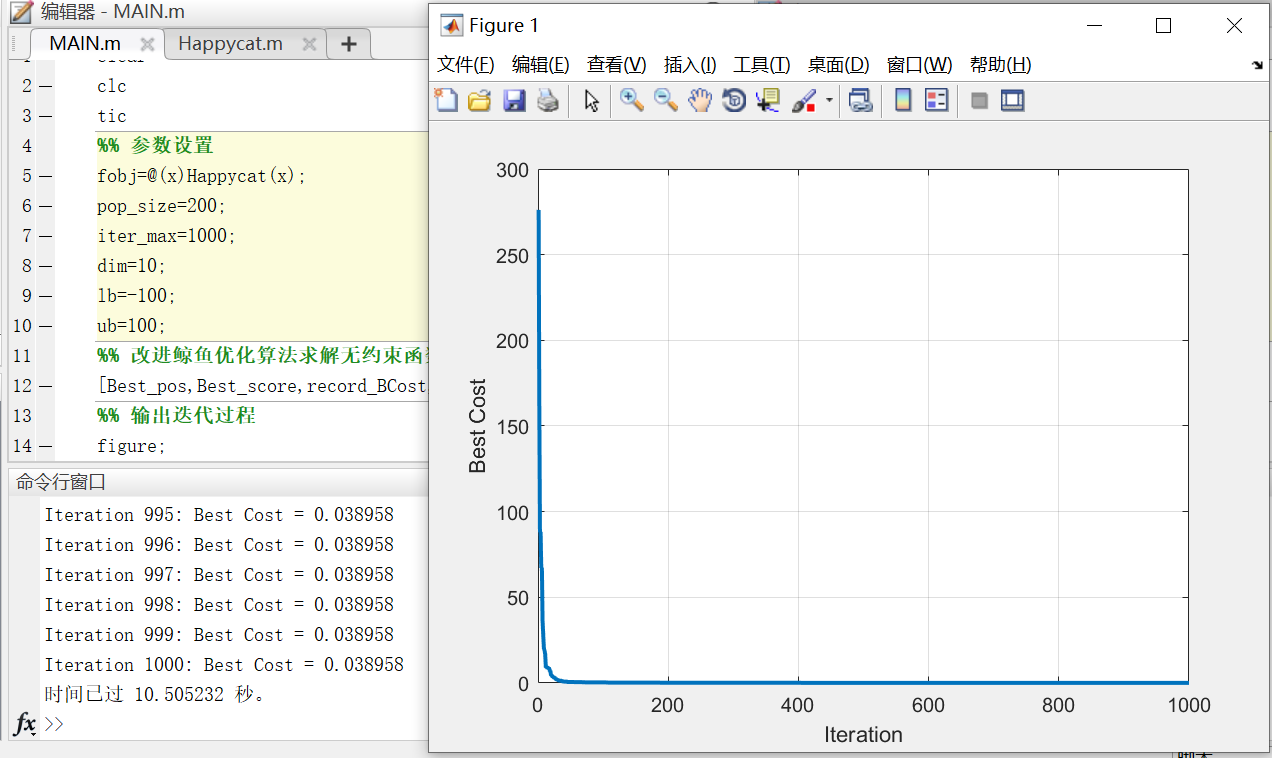
最优值接近0.039，最优解位置如下所示：

（9)Discus Function
$$f_9(\mathbf{x})=10^6{x}_1^2+\sum _{i=2}^D{x}_i^2$$
求解过程如下图所示：

最优值接近0，最优解位置如下所示：

---

参考文献

[1] Sun Y, Wang X, Chen Y, et al. A modified whale optimization algorithm for large-scale global optimization problems[J]. Expert Systems with Applications, 2018, 114: 563-577.

[2] 褚鼎立, 陈红, 王旭光. 基于自适应权重和模拟退火的鲸鱼优化算法[J]. 电子学报, 2019, 47(5): 992-999.

[3] Mohamed A W, Hadi A A, Mohamed A K, et al. Evaluating the performance of adaptive GainingSharing knowledge based algorithm on CEC 2020 benchmark problems[C]//2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020: 1-8.

[4] Lin X, Yu X, Li W. A heuristic whale optimization algorithm with niching strategy for global multi-dimensional engineering optimization[J]. Computers & Industrial Engineering, 2022, 171: 108361.

---

OK，今天就到这里啦，各位可点击下方图片留言，下方图书为作者撰写书籍，助力各位快速入门智能优化算法。

双11期间，京东等各平台购书优惠力度大，科技图书满100减50，各位还在等什么，赶快下单吧。

---

咱们下期再见

近期你可能错过了的好文章

新书上架 | 《MATLAB智能优化算法：从写代码到算法思想》

优化算法 | 灰狼优化算法（文末有福利）

优化算法 | 鲸鱼优化算法

遗传算法（GA）求解带时间窗的车辆路径（VRPTW）问题MATLAB代码

粒子群优化算法（PSO）求解带时间窗的车辆路径问题（VRPTW）MATLAB代码

知乎 | bilibili | CSDN：随心390