hello,大家好。各位可点击左下方阅读原文,访问公众号官方店铺。谨防上当受骗,感谢各位支持!如果链接无法访问,公众号后台回复代码商店,即可获取官方店铺最新链接。
视频讲解链接:

Hello,各位小伙伴。今天为各位分享的是随机规划问题中一个比较经典的问题——报童问题(The Newsvendor Problem)。
问题描述
想象一个报童,每天早上去报纸厂批发一批报纸,然后拿到街上去卖。报纸批发太少,利润就少(这时可视为损失了本该赚到的钱);但批发太多,卖不出去就亏了,虽然报纸厂会提供一定的回收服务,但还是会亏本。(https://zhuanlan.zhihu.com/p/281779832)
那么如何批发报纸能让利润最大呢?报童应该根据需求确定批发数量。但需求具有一定的不确定性,因此需要引入概率进行刻画。
这个问题有以下假设:
- 采购一个商品。
- 在一个采购周期内仅采购一次。
- 采购之时不知道准确的需求,但其概率分布已知。
- 商品会过期。
模型建立
参数
单位采购成本: c c c
零售价: v v v
残值,即商品过期之后的售价: s s s
单位缺货损失: π \pi π
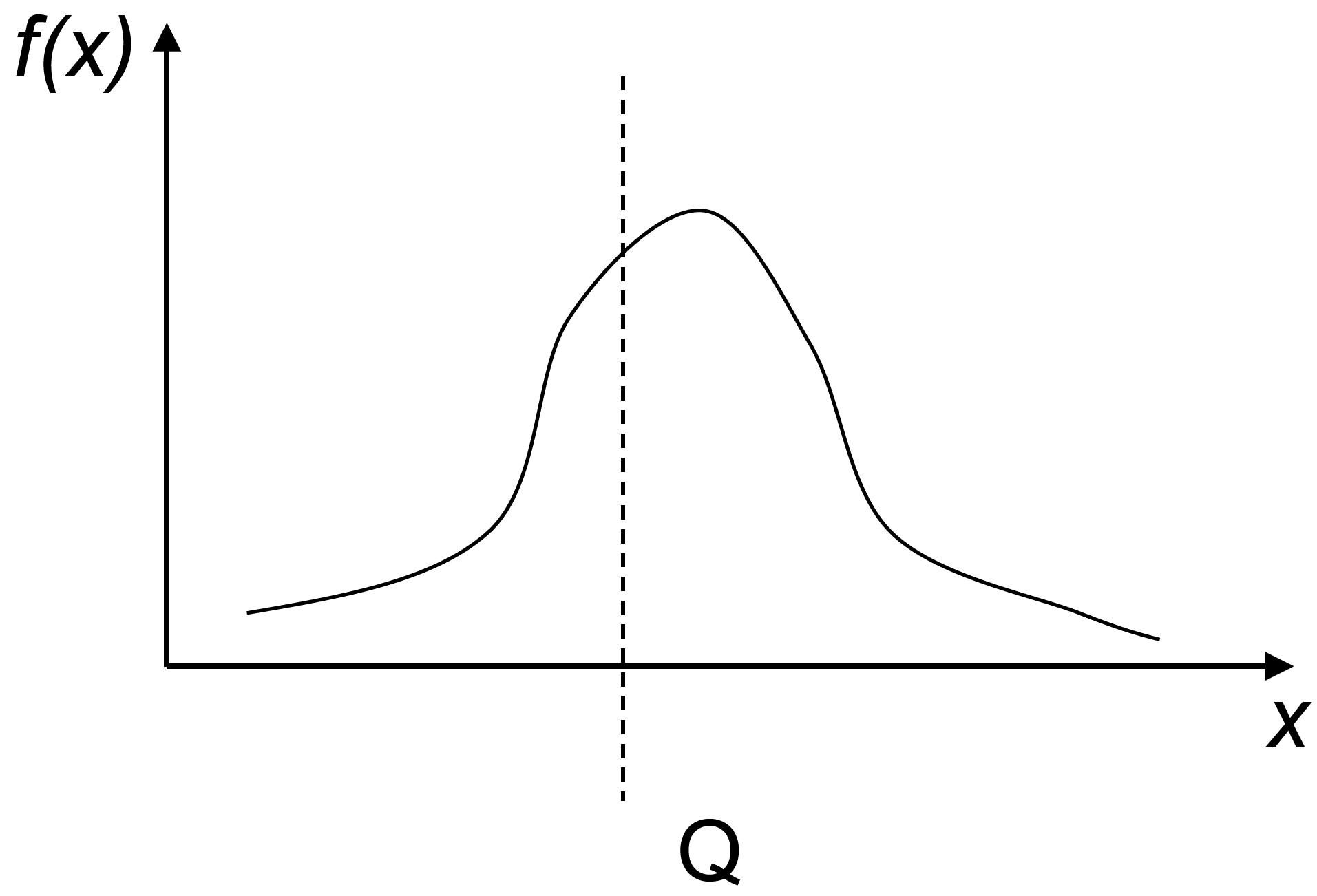
需求:随机变量 x x x,概率密度函数为 f ( x ) f(x) f(x)。其中, x ≥ 0 x\geq0 x≥0,且 ∫ 0 ∞ f ( x ) d x = 1 \int_0^{\infty}f(x) d x=1 ∫0∞f(x)dx=1。
决策变量
订货量: Q Q Q
目标
最大化期望利润 E [ p ( Q ) ] E[p(Q)] E[p(Q)],即包含3部分:
- 扣除采购成本。
- x ≤ Q x \leq Q x≤Q时,销售额和残余价值。
- x > Q x > Q x>Q时,销售额和缺货损失费。
基于上述3部分,期望利润
E
[
p
(
Q
)
]
E[p(Q)]
E[p(Q)]的计算公式如下:
E
[
p
(
Q
)
]
=
−
c
Q
+
v
∫
0
Q
x
f
(
x
)
d
x
+
s
∫
0
Q
(
Q
−
x
)
f
(
x
)
d
x
+
v
∫
Q
∞
Q
f
(
x
)
d
x
−
π
∫
Q
∞
(
x
−
Q
)
f
(
x
)
d
x
(
1
)
\begin{aligned} E[p(Q)]= & -cQ \\ & +v \int_0^Q x f(x) d x+s \int_0^Q(Q-x) f(x) d x \\ & +v \int_Q^{\infty} Q f(x) d x-\pi \int_Q^{\infty}(x-Q) f(x) d x \end{aligned} \quad(1)
E[p(Q)]=−cQ+v∫0Qxf(x)dx+s∫0Q(Q−x)f(x)dx+v∫Q∞Qf(x)dx−π∫Q∞(x−Q)f(x)dx(1)
其中, c Q cQ cQ为采购成本, v ∫ 0 Q x f ( x ) d x v \int_0^Q x f(x) d x v∫0Qxf(x)dx为 x ≤ Q x \leq Q x≤Q时的销售额, s ∫ 0 Q ( Q − x ) f ( x ) d x s \int_0^Q(Q-x) f(x) d x s∫0Q(Q−x)f(x)dx为 x ≤ Q x \leq Q x≤Q时的残余价值, v ∫ Q ∞ Q f ( x ) d x v \int_Q^{\infty} Q f(x) d x v∫Q∞Qf(x)dx为 x > Q x > Q x>Q时的销售额, π ∫ Q ∞ ( x − Q ) f ( x ) d x \pi \int_Q^{\infty}(x-Q) f(x) d x π∫Q∞(x−Q)f(x)dx为 x > Q x > Q x>Q时的缺货损失费。
这里需要注意的一点是, s ∫ 0 Q ( Q − x ) f ( x ) d x s \int_0^Q(Q-x) f(x) d x s∫0Q(Q−x)f(x)dx前的符号为 + + +,实际含义就是假设报童以批发价0.3元(每份)向报社采购当天的报纸,如果报纸在当天没有卖完,他会把报纸以0.05元(每份)的价格卖给废品回收站。
模型求解
变限积分函数求导
因为后续公式推倒过程中会用到变限积分函数求导公式,所以需要先对其进行回顾。
如果函数
f
(
x
)
f(x)
f(x)连续,
ϕ
(
x
)
\phi(x)
ϕ(x)和
φ
(
x
)
\varphi(x)
φ(x)可导,那么变限积分函数的求导公式可表示为:
Φ
′
(
x
)
=
d
d
x
∫
ϕ
(
x
)
φ
(
x
)
f
(
t
)
d
t
=
f
[
φ
(
x
)
]
φ
′
(
x
)
−
f
[
ϕ
(
x
)
]
ϕ
′
(
x
)
(
2
)
\Phi^{\prime}(x)=\frac{d}{d x} \int_{\phi(x)}^{\varphi(x)} f(t) d t=f[\varphi(x)] \varphi^{\prime}(x)-f[\phi(x)] \phi^{\prime}(x) \quad(2)
Φ′(x)=dxd∫ϕ(x)φ(x)f(t)dt=f[φ(x)]φ′(x)−f[ϕ(x)]ϕ′(x)(2)
【定理】如果函数
f
(
x
)
f(x)
f(x)在区间
[
a
,
b
]
[a,b]
[a,b]上连续,则积分上限函数$ \Phi(x)=\int_{a}^{x} f(t)
上具有导数,且导数为
上具有导数,且导数为
上具有导数,且导数为\Phi^{\prime}(x)=\frac{d}{d x} \int_{a}^{x} f(t)=f(x)$。
公式推导
目标是最大化期望利润 E [ p ( Q ) ] E[p(Q)] E[p(Q)],决策变量是订货量 Q Q Q,也就是需要求 d E ( p ( Q ) ) d Q = 0 \frac{d E(p(Q))}{d Q}=0 dQdE(p(Q))=0时的 Q Q Q。
下面详细展示 d E ( p ( Q ) ) d Q \frac{d E(p(Q))}{d Q} dQdE(p(Q))的公式推导过程,首先我们把 E [ p ( Q ) ] E[p(Q)] E[p(Q)]拆分为5块:
① − c Q -cQ −cQ
② + v ∫ 0 Q x f ( x ) d x +v \int_0^Q x f(x) d x +v∫0Qxf(x)dx
③ + s ∫ 0 Q ( Q − x ) f ( x ) d x +s \int_0^Q(Q-x) f(x) d x +s∫0Q(Q−x)f(x)dx
④ + v ∫ Q ∞ Q f ( x ) d x +v \int_Q^{\infty} Q f(x) d x +v∫Q∞Qf(x)dx
⑤ − π ∫ Q ∞ ( x − Q ) f ( x ) d x -\pi \int_Q^{\infty}(x-Q) f(x) d x −π∫Q∞(x−Q)f(x)dx
接下来分别对5块公式依次求导:
①
d
(
−
c
Q
)
d
Q
=
−
c
(
3
)
\frac{d (-cQ)}{d Q}=-c \quad(3)
dQd(−cQ)=−c(3)
②
d
[
+
v
∫
0
Q
x
f
(
x
)
d
x
]
d
Q
=
v
Q
f
(
Q
)
(
4
)
\frac{d [+v \int_0^Q x f(x) d x]}{d Q}=vQf(Q) \quad(4)
dQd[+v∫0Qxf(x)dx]=vQf(Q)(4)
③
d
[
+
s
∫
0
Q
(
Q
−
x
)
f
(
x
)
d
x
]
d
Q
=
d
[
s
∫
0
Q
Q
f
(
x
)
d
x
−
s
∫
0
Q
x
f
(
x
)
d
x
]
d
Q
(
5
)
\frac{d [+s \int_0^Q(Q-x) f(x) d x]}{d Q}=\frac{d [s \int_0^Q Q f(x) d x - s \int_0^Q x f(x) d x]}{d Q} \quad(5)
dQd[+s∫0Q(Q−x)f(x)dx]=dQd[s∫0QQf(x)dx−s∫0Qxf(x)dx](5)
d [ s Q ∫ 0 Q f ( x ) d x − s ∫ 0 Q x f ( x ) d x ] d Q = s d [ Q ∫ 0 Q f ( x ) d x ] d Q − s d [ ∫ 0 Q x f ( x ) d x ] d Q ( 6 ) \frac{d [sQ \int_0^Q f(x) d x - s \int_0^Q x f(x) d x]}{d Q}=s \frac{d [Q \int_0^Q f(x) d x]}{d Q}-s \frac{d [\int_0^Q x f(x) d x]}{d Q} \quad(6) dQd[sQ∫0Qf(x)dx−s∫0Qxf(x)dx]=sdQd[Q∫0Qf(x)dx]−sdQd[∫0Qxf(x)dx](6)
s d [ Q ∫ 0 Q f ( x ) d x ] d Q − s d [ ∫ 0 Q x f ( x ) d x ] d Q = s [ ∫ 0 Q f ( x ) d x + Q f ( Q ) ] − s Q f ( Q ) ( 7 ) s \frac{d [Q \int_0^Q f(x) d x]}{d Q}-s \frac{d [\int_0^Q x f(x) d x]}{d Q}=s[\int_0^Q f(x) d x+Qf(Q)]-sQf(Q) \quad(7) sdQd[Q∫0Qf(x)dx]−sdQd[∫0Qxf(x)dx]=s[∫0Qf(x)dx+Qf(Q)]−sQf(Q)(7)
s [ ∫ 0 Q f ( x ) d x + Q f ( Q ) ] − s Q f ( Q ) = s ∫ 0 Q f ( x ) d x ( 8 ) s[\int_0^Q f(x) d x+Qf(Q)]-sQf(Q)=s\int_0^Q f(x) d x \quad(8) s[∫0Qf(x)dx+Qf(Q)]−sQf(Q)=s∫0Qf(x)dx(8)
d [ + s ∫ 0 Q ( Q − x ) f ( x ) d x ] d Q = s ∫ 0 Q f ( x ) d x = s ( 1 − ∫ Q ∞ f ( x ) d x ) = s − s ∫ Q ∞ f ( x ) d x ( 9 ) \frac{d [+s \int_0^Q(Q-x) f(x) d x]}{d Q}=s\int_0^Q f(x) d x=s(1-\int_Q^{\infty} f(x) d x)=s-s\int_Q^{\infty} f(x) d x \quad(9) dQd[+s∫0Q(Q−x)f(x)dx]=s∫0Qf(x)dx=s(1−∫Q∞f(x)dx)=s−s∫Q∞f(x)dx(9)
④
d
[
+
v
∫
Q
∞
Q
f
(
x
)
d
x
]
d
Q
=
v
d
[
Q
∫
Q
∞
f
(
x
)
d
x
]
d
Q
(
10
)
\frac{d [+v \int_Q^{\infty} Q f(x) d x]}{d Q}=v\frac{d [Q \int_Q^{\infty} f(x) d x]}{d Q} \quad(10)
dQd[+v∫Q∞Qf(x)dx]=vdQd[Q∫Q∞f(x)dx](10)
v d [ Q ∫ Q ∞ f ( x ) d x ] d Q = v [ ∫ Q ∞ f ( x ) d x + Q ( − f ( Q ) ) ] ( 11 ) v\frac{d [Q \int_Q^{\infty} f(x) d x]}{d Q}=v[\int_Q^{\infty} f(x) d x+Q(-f(Q))] \quad(11) vdQd[Q∫Q∞f(x)dx]=v[∫Q∞f(x)dx+Q(−f(Q))](11)
v [ ∫ Q ∞ f ( x ) d x + Q ( − f ( Q ) ) ] = v ∫ Q ∞ f ( x ) d x − v Q f ( Q ) ( 12 ) v[\int_Q^{\infty} f(x) d x+Q(-f(Q))]=v\int_Q^{\infty} f(x) d x - vQf(Q)\quad(12) v[∫Q∞f(x)dx+Q(−f(Q))]=v∫Q∞f(x)dx−vQf(Q)(12)
⑤
d
[
−
π
∫
Q
∞
(
x
−
Q
)
f
(
x
)
d
x
]
d
Q
=
d
[
−
π
∫
Q
∞
x
f
(
x
)
d
x
+
π
Q
∫
Q
∞
f
(
x
)
d
x
]
d
Q
(
13
)
\frac{d [-\pi \int_Q^{\infty}(x-Q) f(x) d x]}{d Q}=\frac{d [-\pi \int_Q^{\infty} x f(x) d x + \pi Q \int_Q^{\infty} f(x) d x]}{d Q} \quad(13)
dQd[−π∫Q∞(x−Q)f(x)dx]=dQd[−π∫Q∞xf(x)dx+πQ∫Q∞f(x)dx](13)
d [ − π ∫ Q ∞ x f ( x ) d x + π Q ∫ Q ∞ f ( x ) d x ] d Q = − π d [ ∫ Q ∞ x f ( x ) d x ] d Q + π d [ Q ∫ Q ∞ f ( x ) d x ] d Q ( 14 ) \frac{d [-\pi \int_Q^{\infty} x f(x) d x + \pi Q \int_Q^{\infty} f(x) d x]}{d Q}=-\pi \frac{d [\int_Q^{\infty} x f(x) d x ]}{d Q} + \pi\frac{d [ Q \int_Q^{\infty} f(x) d x]}{d Q} \quad(14) dQd[−π∫Q∞xf(x)dx+πQ∫Q∞f(x)dx]=−πdQd[∫Q∞xf(x)dx]+πdQd[Q∫Q∞f(x)dx](14)
− π d [ ∫ Q ∞ x f ( x ) d x ] d Q + π d [ Q ∫ Q ∞ f ( x ) d x ] d Q = − π × [ − Q f ( Q ) ] + π ∫ Q ∞ f ( x ) d x + π Q × [ − f ( Q ) ] ( 15 ) -\pi \frac{d [\int_Q^{\infty} x f(x) d x ]}{d Q} + \pi\frac{d [ Q \int_Q^{\infty} f(x) d x]}{d Q}=-\pi \times [-Qf(Q)] +\pi\int_Q^{\infty} f(x) d x + \pi Q \times [-f(Q)] \quad(15) −πdQd[∫Q∞xf(x)dx]+πdQd[Q∫Q∞f(x)dx]=−π×[−Qf(Q)]+π∫Q∞f(x)dx+πQ×[−f(Q)](15)
− π × [ − Q f ( Q ) ] + π ∫ Q ∞ f ( x ) d x + π Q × [ − f ( Q ) ] = π ∫ Q ∞ f ( x ) d x ( 16 ) -\pi \times [-Qf(Q)] +\pi\int_Q^{\infty} f(x) d x + \pi Q \times [-f(Q)] = \pi\int_Q^{\infty} f(x) d x \quad(16) −π×[−Qf(Q)]+π∫Q∞f(x)dx+πQ×[−f(Q)]=π∫Q∞f(x)dx(16)
d [ − π ∫ Q ∞ ( x − Q ) f ( x ) d x ] d Q = π ∫ Q ∞ f ( x ) d x ( 17 ) \frac{d [-\pi \int_Q^{\infty}(x-Q) f(x) d x]}{d Q}= \pi\int_Q^{\infty} f(x) d x \quad(17) dQd[−π∫Q∞(x−Q)f(x)dx]=π∫Q∞f(x)dx(17)
综合对5块公式分别求导结果,即公式(3)(4)(9)(12)(17),则
d
E
(
p
(
Q
)
)
d
Q
\frac{d E(p(Q))}{d Q}
dQdE(p(Q))的求导结果如下:
d
E
(
p
(
Q
)
)
d
Q
=
−
c
+
v
Q
f
(
Q
)
+
s
−
s
∫
Q
∞
f
(
x
)
d
x
+
v
∫
Q
∞
f
(
x
)
d
x
−
v
Q
f
(
Q
)
+
π
∫
Q
∞
f
(
x
)
d
x
(
18
)
\frac{d E(p(Q))}{d Q}=-c+vQf(Q)+s-s\int_Q^{\infty} f(x) d x+v\int_Q^{\infty} f(x) d x - vQf(Q)+\pi\int_Q^{\infty} f(x) d x \quad(18)
dQdE(p(Q))=−c+vQf(Q)+s−s∫Q∞f(x)dx+v∫Q∞f(x)dx−vQf(Q)+π∫Q∞f(x)dx(18)
d E ( p ( Q ) ) d Q = − c + s + ( v − s + π ) ∫ Q ∞ f ( x ) d x ( 19 ) \frac{d E(p(Q))}{d Q}=-c+s+(v-s+\pi) \int_Q^{\infty} f(x) d x \quad(19) dQdE(p(Q))=−c+s+(v−s+π)∫Q∞f(x)dx(19)
令
d
E
(
p
(
Q
)
)
d
Q
=
0
\frac{d E(p(Q))}{d Q}=0
dQdE(p(Q))=0,可推出
−
c
+
s
+
(
v
−
s
+
π
)
∫
Q
∞
f
(
x
)
d
x
=
0
-c+s+(v-s+\pi) \int_Q^{\infty} f(x) d x=0
−c+s+(v−s+π)∫Q∞f(x)dx=0,进而求出最优订货量
Q
⋆
Q^{\star}
Q⋆,即
∫
Q
⋆
∞
f
(
x
)
d
x
=
c
−
s
v
−
s
+
π
(
20
)
\int_{Q^{\star}} ^{\infty} f(x) d x=\frac{c-s}{v-s+\pi} \quad(20)
∫Q⋆∞f(x)dx=v−s+πc−s(20)
因为
∫
0
Q
⋆
f
(
x
)
d
x
+
∫
Q
⋆
∞
f
(
x
)
d
x
=
∫
0
∞
f
(
x
)
d
x
=
1
(
21
)
\int_{0} ^{Q^{\star}} f(x) d x+\int_{Q^{\star}} ^{\infty} f(x) d x =\int_{0} ^{\infty} f(x) d x=1 \quad(21)
∫0Q⋆f(x)dx+∫Q⋆∞f(x)dx=∫0∞f(x)dx=1(21)
所以
∫
0
Q
⋆
f
(
x
)
d
x
=
1
−
∫
Q
⋆
∞
f
(
x
)
d
x
=
1
−
c
−
s
v
−
s
+
π
=
v
+
π
−
c
v
+
π
−
s
(
22
)
\int_{0} ^{Q^{\star}} f(x) d x=1-\int_{Q^{\star}} ^{\infty} f(x) d x=1-\frac{c-s}{v-s+\pi}=\frac{v+\pi-c}{v+\pi-s} \quad(22)
∫0Q⋆f(x)dx=1−∫Q⋆∞f(x)dx=1−v−s+πc−s=v+π−sv+π−c(22)
至此,公式推导完毕。
小结
已知单位采购成本
c
c
c、零售价
v
v
v、残值
s
s
s、单位缺货损失
π
\pi
π、需求
x
x
x,概率密度函数
f
(
x
)
f(x)
f(x),则使利润最大化的最优订货量
Q
⋆
Q^{\star}
Q⋆的计算公式如下:
∫
0
Q
⋆
f
(
x
)
d
x
=
v
+
π
−
c
v
+
π
−
s
(
23
)
\int_{0} ^{Q^{\star}} f(x) d x=\frac{v+\pi-c}{v+\pi-s} \quad(23)
∫0Q⋆f(x)dx=v+π−sv+π−c(23)
如果
f
(
x
)
f(x)
f(x)为正太分布函数,均值和标准差分别记为
μ
\mu
μ和
σ
\sigma
σ,且
∫
0
Q
⋆
f
(
x
)
d
x
=
A
\int_{0} ^{Q^{\star}} f(x) d x=A
∫0Q⋆f(x)dx=A,那么根据正太分布变换成标准正太分布(均值为0,标准差为1)的变换公式
z
=
X
−
μ
σ
z=\frac{X-\mu}{\sigma}
z=σX−μ,则
Φ
(
z
)
=
A
\Phi(z)=A
Φ(z)=A,然后通过查标准正太分布表计算出
z
z
z,进而计算出
Q
⋆
Q^{\star}
Q⋆,即
z
=
Q
⋆
−
μ
σ
z=\frac{Q^{\star}-\mu}{\sigma}
z=σQ⋆−μ。
Q
⋆
=
z
×
σ
+
μ
(
24
)
Q^{\star}=z \times {\sigma}+\mu \quad(24)
Q⋆=z×σ+μ(24)

https://www.shuxuele.com/data/standard-normal-distribution-table.htm
实际案例
现有一批商品零售价为25元,单位采购成本为20元,单位剩余处理费为0.5元(需花钱处理),需求服从正态分布,均值为300个,方差为50个,单位缺货损失为5元,问商品订货量为多少才能使得商品期望利润最大?
根据公式(23),
∫
0
Q
⋆
f
(
x
)
d
x
=
v
+
π
−
c
v
+
π
−
s
=
25
+
5
−
20
25
+
5
+
0.5
=
0.328
\int_{0} ^{Q^{\star}} f(x) d x=\frac{v+\pi-c}{v+\pi-s}=\frac{25+5-20}{25+5+0.5}=0.328
∫0Q⋆f(x)dx=v+π−sv+π−c=25+5+0.525+5−20=0.328
这里需要注意的是,因为剩余商品需要花钱处理,所以这里的残值为负数。
查正太分布表得:
z
=
−
0.445
z=-0.445
z=−0.445,则由公式(24),可计算出最优订货量
Q
⋆
Q^{\star}
Q⋆
Q
⋆
=
z
×
σ
+
μ
=
−
0.445
×
50
+
300
=
277.75
≈
278
Q^{\star}=z \times {\sigma}+\mu=-0.445 \times 50 + 300 = 277.75 \approx 278
Q⋆=z×σ+μ=−0.445×50+300=277.75≈278
MATLAB代码如下:
%% The Newsvendor Problem
clear
clc
c=20; %单位采购成本
v=25; %零售价
s=-0.5; %残值,即商品过期之后的售价。题目中因为剩余商品需要花钱处理,所以这里的残值为负数。
pi=5; %单位缺货损失
mu=300; %需求均值
sigma=50; %需求标准差
integralValue=(v+pi-c)/(v+pi-s); %最优订货量Qstar积分值
z=norminv(integralValue); %求z值,z=(Qstar-mu)/sigma
Qstar=ceil(z*sigma+mu); %最优订货量
参考
- 《生产存储理论》课程-黄敏
- 报童问题及其求解-https://zhuanlan.zhihu.com/p/281779832
- 随机规划模型(Stochastic Programming Models)-https://zhuanlan.zhihu.com/p/160994724
- 报童问题The Newsvendor Problem-https://zhuanlan.zhihu.com/p/473728474
- 报童问题 (The Newsvendor Problem)-https://blog.csdn.net/qx3501332/article/details/104995161
想快速入门智能优化算法的小伙伴可以阅读我们的书籍,本书对算法的讲解详细易懂,对代码的注释也十分完备,想要入手此书的小伙伴可以抓紧入手哦!

京东自营购买链接:
https://item.jd.com/13422442.html
当当自营购买链接
http://product.dangdang.com/29301483.html
咱们下期再见
近期你可能错过了的好文章
新书上架 | 《MATLAB智能优化算法:从写代码到算法思想》
算法自学 | 优化算法书籍+代码+网站+推文一站式合集(上)
遗传算法(GA)求解带时间窗的车辆路径(VRPTW)问题MATLAB代码
粒子群优化算法(PSO)求解带时间窗的车辆路径问题(VRPTW)MATLAB代码
知乎 | bilibili | CSDN:随心390
























 5130
5130

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








