蒙特卡洛方法

定义

蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。

起源

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的"曼哈顿计划"计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。. 数学家冯·诺伊曼用驰名世界的赌城-摩纳哥的Monte Carlo来命名这种方法，为它蒙上了一层神秘色彩。在这之前，蒙特卡罗方法就已经存在。

工作过程

• 1、用蒙特卡罗方法模拟某一过程时，需要产生各种概率分布的随机变量。
• 2、用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。

应用领域

蒙特卡罗方法在金融工程学，宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算、核工程)等领域应用广泛。

蒙特卡罗分子模拟计算步骤

使用蒙特·卡罗方法进行分子模拟计算是按照以下步骤进行的：

• 1．使用随机数发生器产生一个随机的分子构型。

• 2．对此分子构型的其中粒子坐标做无规则的改变，产生一个新的分子构型。

• 3．计算新的分子构型的能量。

• 4．比较新的分子构型于改变前的分子构型的能量变化，判断是否接受该构型。

• 若新的分子构型能量低于原分子构型的能量，则接受新的构型，使用这个构型重复再做下一次迭代。

• 若新的分子构型能量高于原分子构型的能量，则計算玻尔兹曼因子，并产生一个随机数。

1）若这个随机数大于所计算出的玻尔兹曼因子，则放弃这个构型，重新计算。

2）若这个随机数小于所计算出的玻尔兹曼因子，则接受这个构型，使用这个构型重复再做下一次迭代。

5．如此进行迭代计算，直至最后搜索出低于所给能量条件的分子构型结束。

项目管理

项目管理中蒙特·卡罗模拟方法的一般步骤是：

1．对每一项活动，输入最小、最大和最可能估计数据，并为其选择一种合适的先验分布模型；

2．计算机根据上述输入，利用给定的某种规则，快速实施充分大量的随机抽样

3．对随机抽样的数据进行必要的数学计算，求出结果

4．对求出的结果进行统计学处理，求出最小值、最大值以及数学期望值和单位标准偏差

5．根据求出的统计学处理数据，让计算机自动生成概率分布曲线和累积概率曲线(通常是基于正态分布的概率累积S曲线)

6．依据累积概率曲线进行项目风险分析。

力学

在力学中，蒙特卡罗方法多被用来求解稀薄气体动力学问题，其中最为成功的是澳大利亚G.A.伯德等人发展的直接模拟统计试验法。此法通过在计算机上追踪几千个或更多的模拟分子的运动、碰撞及其与壁面的相互作用，以模拟真实气体的流动。它的基本假设与玻耳兹曼方程一致，但它是通过追踪有限个分子的空间位置和速度来代替计算真实气体中分布函数。模拟的相似条件是流动的克努曾数（Kn）相等，即数密度与碰撞截面之积保持常数。对每个分子分配以记录其位置和速度的单元。在模拟过程中分别考虑分子的运动和碰撞，在此平均碰撞时间间隔内，分别计算分子无碰撞的运动和典型碰撞。若空间网格取得足够小，其中任意两个分子都可以互相碰撞。具体决定哪两个刚体分子相撞，是随机取一对分子，计算它们的相对速度，根据此值与最大相对速度的比值和随机取样比较的结果，来决定该对分子是否入选。碰撞后分子的速度根据特定分子模型的碰撞力学和随机取样决定。分子与壁面碰撞后的速度，则根据特定的反射模型和随机取样决定。对于运动分子的位置和速度的追踪和求矩可以得出气体的密度、温度、速度等一些感兴趣的宏观参量。而对于分子与壁面间的动量和能量交换的记录则给出阻力、举力和热交换系数等的数学期望值。

案例

1.π的计算

正方形内部有一个相切的圆，它们的面积之比是π/4


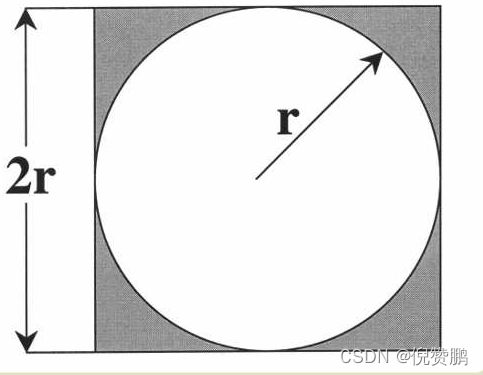
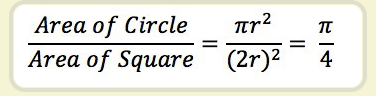
在这个正方形内部，随机产生10000个点（即10000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。

如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。通过R语言脚本随机模拟30000个点，π的估算值与真实值相差0.07%。

2.积分的计算

计算函数 y = x2 在 [0, 1] 区间的积分，就是求出下图红色部分的面积。

这个函数在 (1,1) 点的取值为1，所以整个红色区域在一个面积为1的正方形里面。在该正方形内部，产生大量随机点，可以计算出有多少点落在红色区域（判断条件 y < x2）。这个比重就是所要求的积分值。
用Matlab模拟100万个随机点，结果为0.3328。

3.交通堵塞

蒙特卡罗方法不仅可以用于计算，还可以用于模拟系统内部的随机运动。下面的例子模拟单车道的交通堵塞。
根据 Nagel-Schreckenberg 模型，车辆的运动满足以下规则。

在一条直线上，随机产生100个点，代表道路上的100辆车，另取概率 p 为 0.3

上图中，横轴代表距离（从左到右），纵轴代表时间（从上到下），因此每一行就表示下一秒的道路情况。

可以看到，该模型会随机产生交通拥堵（图形上黑色聚集的部分）。这就证明了，单车道即使没有任何原因，也会产生交通堵塞。

import numpy as np  
import matplotlib.pyplot as plt  
import matplotlib.patches as mpatches  
import scipy.integrate as integrate   
  
''''' 
Monte Carlo method (蒙特卡洛方法，也有翻译成“蒙特卡罗方法”）是以概率和统计的理论、方法为基础的一种数值计算方法， 
将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解，故又称随机抽样法或统计试验法。 
上述就是蒙特卡洛方法的基本概念，比较抽象，下面结合实际工作中的理解，谈一谈对蒙特卡洛方法的一些认识。 
 
（1）数学家冯·诺伊曼（计算机之父）在20世纪40年代中期用驰名世界的赌城摩纳哥的蒙特卡洛来命名这种方法， 
    说明该方法与赌博中的随机性、概率性有着天然而密切的联系。几乎涉及到概率相关的复杂数值计算的领域（计算物理、经济金融、统计学、机器学习等）。 
 
（2）蒙特卡洛是一种方法或者说策略，没有什么高深的理论支撑（如果有理论也就只有概率论或统计学中的大数定律了）。 
    蒙特卡洛的基本原理简单描述是先大量模拟，然后计算一个事件发生的次数，再通过这个发生次数除以总模拟次数，得到想要的结果。 
    例如模拟投N次（随机样本数），统计同时出现6的次数C(C/N即是计算结果)。 
 
（3）蒙特卡洛方法可应用在很多场合（求的是近似解）。模拟样本数越大，越接近与真实值，同时样本数增加会带来计算量的大幅上升。 
 
    实例：蒙特卡洛方法求函数y=x^2在[0,2]区间的积分（即求面积）。 
        备注：直接用数学中的定积分公式算更简单精确。 
    该红色区域在一个2×4的正方形里面。使用蒙特卡洛方法，随机在这个正方形里面产生大量随机点（数量为N）， 
    计算有多少点（数量为count）落在红色区域内（判断条件为y<x2），count/N就是所要求的积分值，也即红色区域的面积。 
'''  
np.random.seed(12345)  
x = np.linspace(0, 2, 1000)  # 绘制曲线  
y = x ** 2  
plt.plot(x, y)  
plt.fill_between(x, y, where=(y > 0), color='red', alpha=0.5)  # 填充颜色  
# plt.show()  
  
#模拟1000个随机点  
N = 1000  
points = [[xy[0] * 2, xy[1] * 4] for xy in np.random.rand(N, 2)]  
plt.scatter([x[0] for x in points], [x[1] for x in points], s=5, c=np.random.rand(N), alpha=0.5)  
plt.show()  
  
#计算落在红色区域的比重  
count = 0  
for xy in points:  
    if xy[1] < xy[0] ** 2:  
        count += 1  
print((count / N) * (2 * 4))  # 2.752  
print(integrate.quad(lambda x: x ** 2, 0, 2)[0])  
  
''''' 
蒙特卡洛方法有一定的误差，误差的大小与模拟的样本大小直接相关，模拟样本越大，误差越小，但计算量也会大幅上升。 
对于简单问题来说，蒙特卡洛是个“笨”办法。 
但对于涉及复杂、不可解析函数或概率分布的模拟及计算，蒙特卡洛方法是个有效的方法，有时甚至是唯一可行的方法。 
'''  
  
''''' 
实例2：套圈圈的游戏，想过为什么你总是套不上吗？用蒙特卡洛方法来算一算。 
1.设物品中心点坐标为（0,0），物品半径为5cm。 
'''  
#  
circle_target = mpatches.Circle([0, 0], radius=5, edgecolor='r', fill=False)  
plt.xlim(-80, 80)  
plt.ylim(-80, 80)  
plt.axes().add_patch(circle_target)  
# plt.show()  
  
''''' 
2.设投圈半径8cm，投圈中心点围绕物品中心点呈二维正态分布，均值μ=0cm，标准差σ=20cm，模拟1000次投圈过程。 
上图中红圈为物品，散点图为模拟1000次投圈过程中，投圈中心点的位置散布。 
3.计算1000次投圈过程中，投圈套住物品的占比情况。 
'''  
N = 1000  
u, sigma = 0, 20  
points = sigma * np.random.randn(N, 2) + u  
plt.scatter([x[0] for x in points], [x[1] for x in points], c=np.random.rand(N), alpha=0.5)  
plt.show()  
  
print(len([xy for xy in points if xy[0] ** 2 + xy[1] ** 2 < (8 - 5) ** 2]) / N)  
#输出结果：0.009，即投1000次，有9次能够套住物品，是小概率事件，知道你为什么套不住了吧。  
''''' 
蒙特卡洛方法本身不是优化方法， 
与遗传算法、粒子群算法等智能优化算法有相似之处，比如都属于随机近似方法，都不能保证得到最优解等， 
但它们也有着本质的差别。 
一是层次不一样，蒙特卡洛只能称之为方法，遗传算法等则属于仿生智能算法，比蒙特卡洛方法要复杂。 
二是应用领域不同，蒙特卡洛是一种模拟统计方法，如果问题可描述成某种统计量的形式，就可以用蒙特卡洛方法解决； 
遗传算法等适用于大规模的组合优化问题（选址问题、排班问题、管理调度、路线优化）等，及复杂函数求最值、参数优化等。 
'''