对于logistic模型,我们经常见到的形式是这样子的dNdt=r∗N∗(1−NK)\frac{dN}{dt}=r*N*(1-\frac{N}{K})dtdN=r∗N∗(1−KN)
其中N为种群生物数量(或密度),r为固定增长率,K为种群环境容纳量
我们可以求它的原函数:
先分离变量1r∗N∗(1−NK)∗dN=1dt\frac{1}{r*N*(1-\frac{N}{K})}*dN=1 dtr∗N∗(1−KN)1∗dN=1dt
两边积分∫1r∗N∗(1−NK)∗dN=∫1dt\int\frac{1}{r*N*(1-\frac{N}{K})}*dN=\int 1 dt∫r∗N∗(1−KN)1∗dN=∫1dt
整理一下1r∫KN∗(K−N)dN=∫1dt\frac{1}{r}\int \frac{K}{N*(K-N)}dN=\int 1 dtr1∫N∗(K−N)KdN=∫1dt
拆开分式1r∫1N+1K−NdN=∫1dt\frac{1}{r}\int \frac{1}{N}+\frac{1}{K-N}dN=\int 1 dtr1∫N1+K−N1dN=∫1dt
计算积分1r(lnN−ln(K−N)+C1)=t+C2\frac{1}{r} \left(ln{N}-ln(K-N)+C_1 \right)=t+C_2r1(lnN−ln(K−N)+C1)=t+C2
整理一下NK−N=ert+rC2−C1\frac{N}{K-N}=e^{rt+rC_2-C_1}K−NN=ert+rC2−C1
设C=rC2−C1C=rC_2-C_1C=rC2−C1
有NK−N=ert+C\frac{N}{K-N}=e^{rt+C}K−NN=ert+C
即N=Kert+C1+ert+C,也即N=K1+e−rt−CN=\frac{Ke^{rt+C}}{1+e^{rt+C}},也即N=\frac{K}{1+e^{-rt-C}}N=1+ert+CKert+C,也即N=1+e−rt−CK
若我们假设t=0t=0t=0时刻N=N0N=N_0N=N0
则有N0=K1+e−CN_0=\frac{K}{1+e^{-C}}N0=1+e−CK
整理得C=ln(N0K−N0)C=ln(\frac{N_0}{K-N_0})C=ln(K−N0N0)
于是结论有N=K1+e−rt−C(Nt=0=N0,C=ln(N0K−N0))N=\frac{K}{1+e^{-rt-C}}\quad(N_{t=0}=N_0,C=ln(\frac{N_0}{K-N_0}))N=1+e−rt−CK(Nt=0=N0,C=ln(K−N0N0))
函数图像如下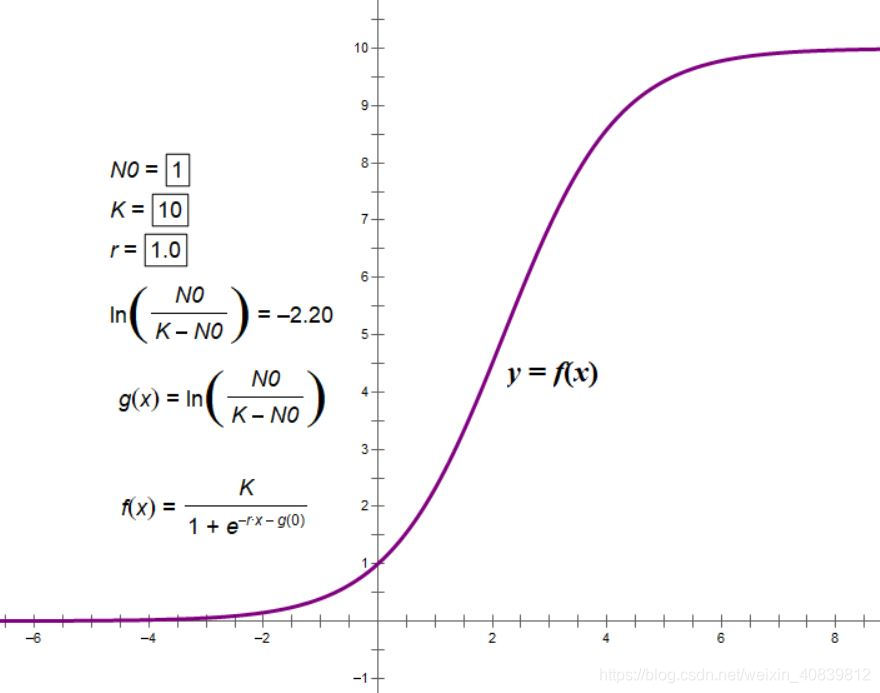
种群数量变化模型logistic模型的种群数量函数
最新推荐文章于 2024-09-20 21:42:59 发布
 本文深入解析了Logistic模型的数学原理,详细推导了模型的原函数,解释了种群生物数量随时间变化的规律,并给出了模型的具体应用案例。
本文深入解析了Logistic模型的数学原理,详细推导了模型的原函数,解释了种群生物数量随时间变化的规律,并给出了模型的具体应用案例。
























 1466
1466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








