新智元报道
编辑:编辑部
【导读】关于「零点猜想」问题,大海里的针我没捞到, 但海底地貌我探得差不多了。
一支马克笔,一张小白板。
刚刚,张益唐教授现身北大,在B站的直播平台上,给广大网友上了一堂大师级数学课。
授课内容大家都知道了,就是最近张教授刚刚取得的新突破:朗道-西格尔零点猜想问题。
这是张益唐亲自对自己前不久的那篇论文的全面解析。
全程40分钟,无废话无尿点,硬核知识拉满,信息密度极大。

文字实录
首先,我得介绍一下这个问题本身。
虽然我的论文已经挂到aXiv上了,但还是得介绍一下:什么叫朗道-西格尔零点呢?
对于这个狄利克雷L函数,L(s,χ)的原始定义是这样的:
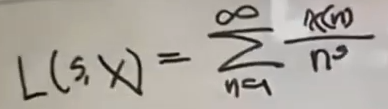
分子是χ(n)这个值,分母就是n的s次方。
此时,我们只考虑s是个实数的时候,也就是说s=1的时候,它不等于0。那么s<1的时候,就是说比1稍微小一点, 它有没有可能等于0?
这个问题因为牵扯到很多数论的东西,所以很重要,但始终没有人能够解决。
只考虑L(s,χ)不等于0的情况——
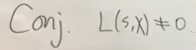
如果s比1稍微小一点,这个分母是比较可控的,c是个常数
![]()
这是一个猜想,我们说这个猜想比黎曼假设要弱得多,至少是对L函数的黎曼猜想(广义黎曼猜想)。广义黎曼猜想是说这个S的实部大于1/2的话不等于0,但就只是很接近1的时候不等于0。
这个猜想本质上说就是朗道-西格尔零点问题。
这个问题,就是要证明这样的一类零点是不存在的(尤其是实零点,虚零点还容易一点)。
那么现在我们能做到什么程度呢?应该说本质上我们至少证明了这样一个东西

这个2024就像孪生素数里面的情况一样,是可以改进的。
前两天消息刚传出来的时候,很多人不是做数学的,所以不理解这个朗道-西格尔零点问题解决的是什么,甚至有人以为就是证明了黎曼假设是错的。
这个我得说一句:我可没有这个本事(笑)。我只是在一定范围内部分地证明了黎曼假设应该是对的。如果说我推翻了黎曼假设,那应该是没什么人会相信。
在这篇论文第二节的结尾,我引进了三个proposition,都是不等式。这三个不等式合在一起后,如果说朗道-西格尔零点存在的话,就可以得出一个矛盾。
而这个讲起来就是一个非常非常复杂的东西,要讲清楚也不容易,但是我可以讲一讲,这里面它的一个基本思路,讲一下它最后的归结。最后就是归结到这样一个事情上——
![]()
怎么会归结到这个事情上呢?
对于一个有限的实数序列χn,怎么样证明它并不是非负的?

这就是要去证明其中有一个(至少有一个)χn是小于0的。
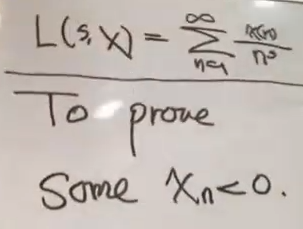
说起来这个问题是什么呢?有点不着边际。
但事实上很有意思,在数论中,特别是解析中,很多东西可以归结到这么一个问题。
于是我们就需要发展一个技巧,来证明这个东西是不等于0的。

第一个例子,我们就说一个偶数N(一个比较大的偶数),我们用ρ(n)定义这个素数的特征函数,都是定义在正整数上。
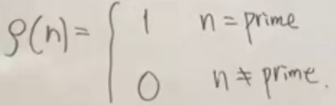
如果n是素数,ρ(n)等于1,如果n不是素数,ρ(n)就等于0。
就可以得到
![]()
我们说这个序列会什么样?
一般情况下,它可能等于1,也可能等于0, 但它有没有可能是负的呢?
很明显如果ρ(n)是负的,它必须等于-1,而且他负的充要条件是ρ(n)和ρ(N-n)都是素数。这时候χn才可能是负的,正好等于-1。
很明显,N永远是等于n+(N-n),也就是N就是一个素数加上另外一个素数。
就是说如果在这个序列(1<n<N)里,有某一个χn是小于0的话,充要条件是N是两个素数的和。

所以哥德巴赫猜想最后就可以归结到我们来构建这样一个有限序列,这里头是不是有这么一个小于0的数?如果有的话,哥德巴赫猜想就是对的。
那么,是不是还有别的问题也是这样呢?
其实假如我们对孪生素数猜想给出一个弱结果,那么也会是这样的,也就是造成这么一个χn。
它这个定义也是
![]()
如果这里面有两个是素数,那么χn就严格小于0;如果只有一个素数,那么就等于0;如果没有就大于0。
所以在这样一个序列里面,我们可以人为地把n的范围给它确定,里面有没有负的?这就是我们在孪生素数研究下取得的突破。我们的出发点就是这个东西。
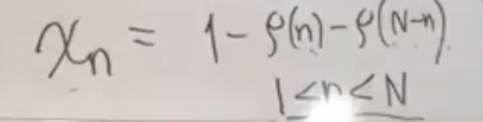
话再说回来,怎么样去证明某一个χn是小于0,我们就给出了一个很简单的数列,哪怕里面有10000个数,我们也可以写出来这里面是不是有一个是负的,这很简单。
但我们这里考虑的都是理论性的问题,N是一个很大的数,怎么样去定义这个东西等于0。
这是第一个例子。实际上它既包括了哥德巴赫猜想,也包括了孪生素数弱结果的研究。
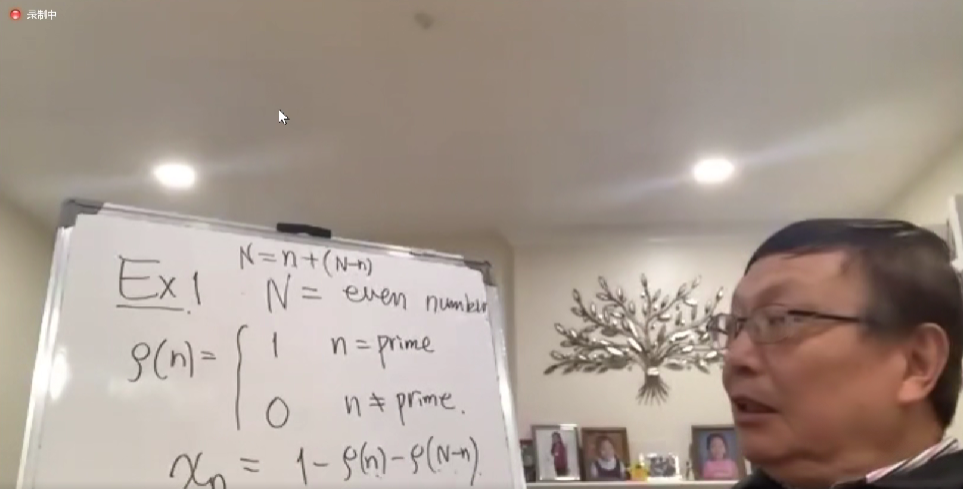
第二个例子是一个纯公式的例子,它跟我要做的事情是相关的。
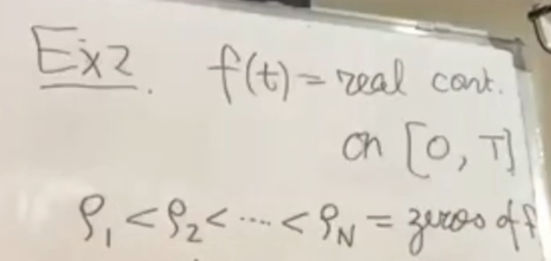
如果有一个Assumption,我们就假定ρ(n+1)>ρn+c——

也就是说零点的间隔比c要大,那么我们也可以把它归结成——
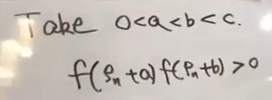
其中,f(ρn+a) f(ρn+b)它一定是正的。
为什么这么说呢?因为随便一个ρn,从ρn到ρn+c之间,他一定没有零点。而ρn+a和ρn+b一定在这段之间,因为f是连续函数,所以他们的乘积一定是大于等于0的。
所以如果我们要证明assumption是不对的,可能有零点的间隔比c要小。如果我能够证明有一个χn是负的,只要证明它≤0,那这个assumption就错了。
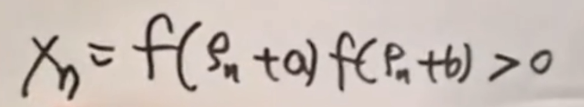
如果我想证明的话,我就得去弄。

那么究竟我们需要怎么处理这个问题呢?
要证明有限的实数序列不是非负的,里面至少有一个是严格小于0的,怎么去证明呢?

我们常用的处理方法是这样:
我们找一组新的实数序列{yn},它要满足两个条件。第一:yn≥0,第二个:∑xnyn<0。只要能找到这样一组yn,这问题就解决了。

那这里头肯定有一项是严格小于0的,但yn是大于等于0,那么xn必须是小于0的。这就解决了传统要去做的事情。
可是怎么去选yn呢?这就牵扯到整个筛法发展的历史了。
最早是挪威数学家Brown在一个世纪前,应该在1917、18年的时候他找到了一组yn。这组yn的表述是很复杂的,但满足这类条件。
然后他用这个条件能推出9+9,在当时来讲是不可思议的,是一个惊人的构造。
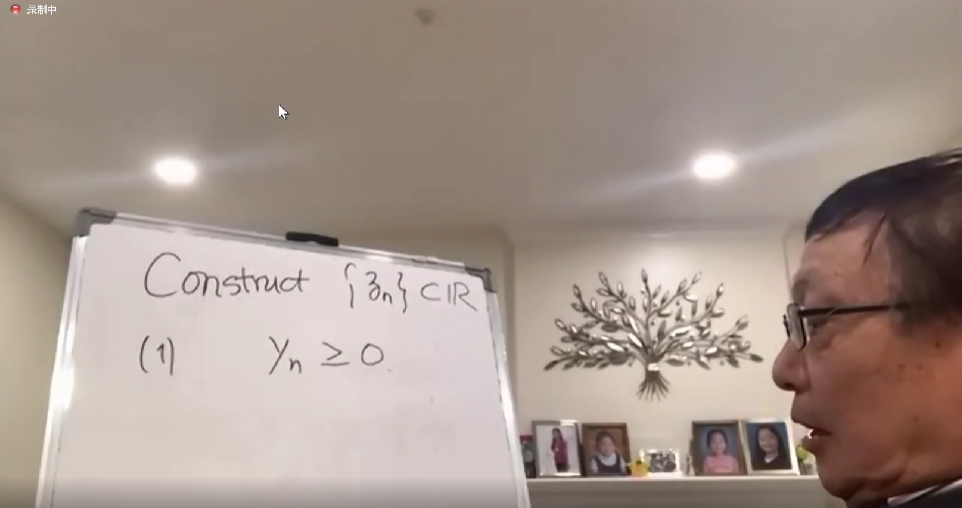
后来,到了20世纪40年代末,另外一个挪威数学家叫塞尔伯格,他想得就比较简单,他说干脆我就去构造一组实数序列zn,zn是实数就行,没有任何限制。

然后把yn取成zn平方,于是第一个条件就自然满足了——实数的平方必然是大于等于0的。
于是问题就变成了,能不能得出下式小于0?
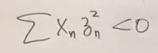
这里要牵扯到孪生素数猜想最近的进步,特别是梅纳德最近的贡献(他最近得了菲尔兹数学奖)。
xn的取值与孪生数有关,我们希望这里面至少有一个是负的,然后是求和。

在我之前有三个数学家,他们找到一组zn,能够证明这个和非常切近0,并且可以做到让ε任意小。
但是小于0这一步他们怎么也跨不过去。
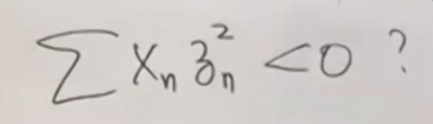
而这里的主要障碍就是,他们要用到素数在等差级数里的分布,那里头有个限制就是有一个exponent指数,它不能超过1/2,否则余项就控制不住。
于是他们就跨在这个边上,用他们的话来说差一根头发丝就能跨过去了,但这个头发丝就没跨过去。
然后再下一步是我的工作:
我的工作从单独意义上来讲,在等差级数分布的问题上,应该是第一次突破了指数等于1/2的界限,就是说可以把这个指数取到比1/2再大一点。但我用的zn基本上还是他们引进的。
后来梅纳德就把这个问题改进了一大步,他引进了一种新的zn,最后能够证出这个孪生素数的弱形式,最后我们都是归结到这样一个不等式。
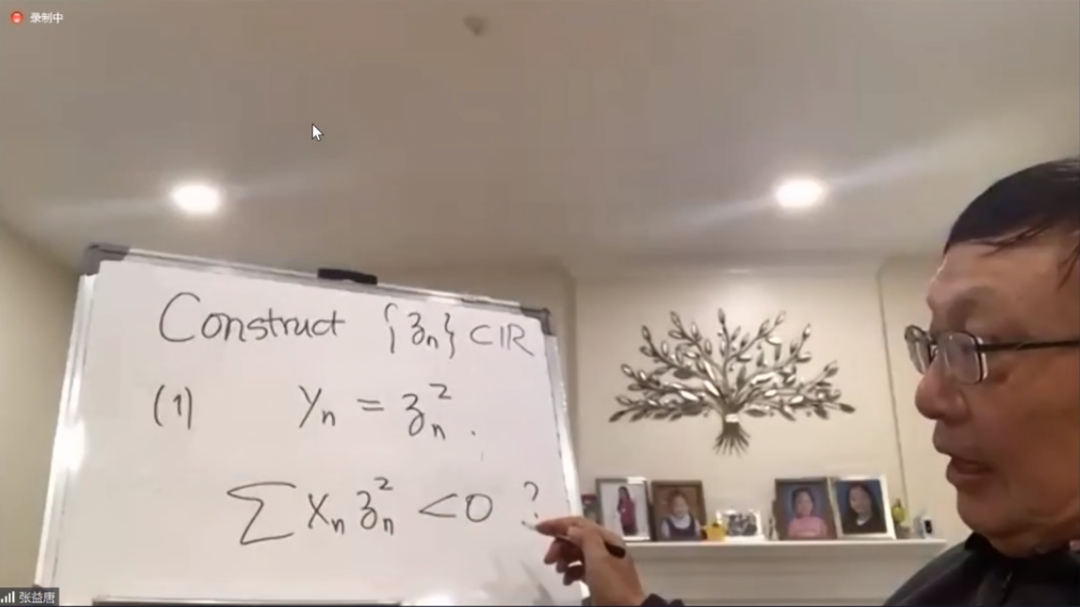
下面我们再回到朗道-西格尔零点,
我们也去构造像例2中实的连续函数,如果两个点中间没有零点的话,它们就是同号,它们的乘积应该就是非负的。

在论文的引理2.3中,我给出了这么一个东西,那么我就是要证明这么一个事情——
如果存在朗道-西格尔零点,就推出
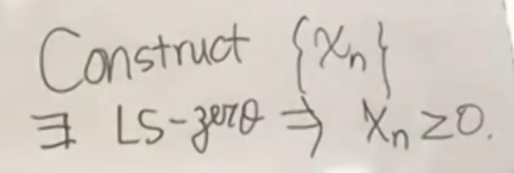
我想证明这个东西
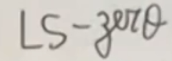
是错的,也就是说我能证明
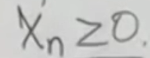
这个里面有一个是负的话,就可以了。

我花了很长时间,去证明下面这个结果是小于0的。

我找了很多很多这样的东西,发现一些非常有意思的事情:我没能直接证明它是小于0的,但我发现对很多zn它接近0。
它会小于一个ε乘上一个东西,而这个ε可以尽量小,我发现很多这样的zn。所以就差一点。
当孪生素数猜想出来时,有人说我是大海捞针。但实际上不太对,孪生素数实际上我没有去捞什么针。
但是去找这个zn,我确实是在大海捞针。
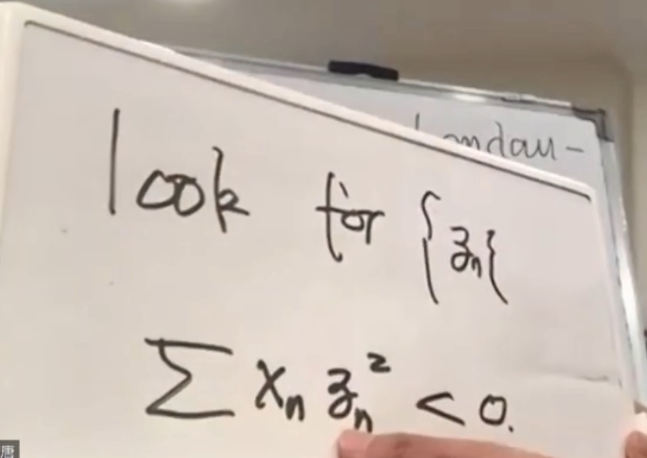
我试了很多很多东西,包括用到像变分法啊,用积分方程去找最大特征根啊,最后都是有一个问题:你可以在不同角度去找zn,找出来以后都是小于一个ε乘上一个数字,但这个ε你就是跨不过去,有点像我在做孪生素数时那样。
那最后是怎么去解决的呢?
这里我就想提到我在一开始给出的第一个公式。我的一个最初的想法,就是最关键的一步,我为什么能达到一个这样的证明。
第一步,我找到两组序列,都可以写成是这种形式——

这两组序列我都可以证明……(这里还是把它写出实数形式)
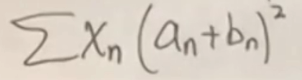
这个东西我不能证明它小于0,实际上严格算它就是不小于0,但可以证明它非常接近于0。

同时呢,我也可以证明对于cn和dn,下面这个结果也是接近于0的。
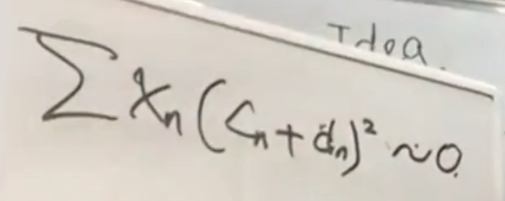
而且呢,证明这两个关系式虽然看起来结果是一样的,但证明的方法是完全不一样的,是两种完全不同的treatment。
于是,我们又有一种方式证明这个东西接近0,但不能证明它小于0。
那么这两组序列有没有可能发生冲突呢?有冲突,就能给出一个矛盾。于是我就用了这样一个关系式。
出发点我们还是假定xn大于等于0。
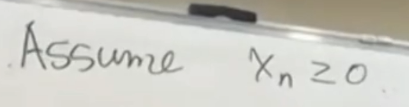
然后我们用这样一个关系式,也就是一开始写的那个。
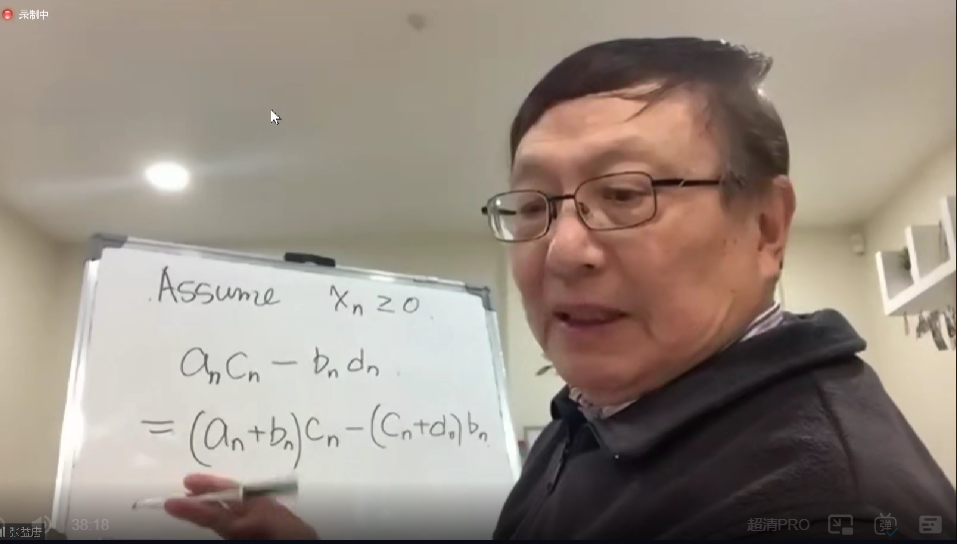
因为这个χn是非负的,χn我们就不需要取绝对值了。
我们再用这个关系式取一个绝对值,这里可以全部都取绝对值,减号就变成加号了。
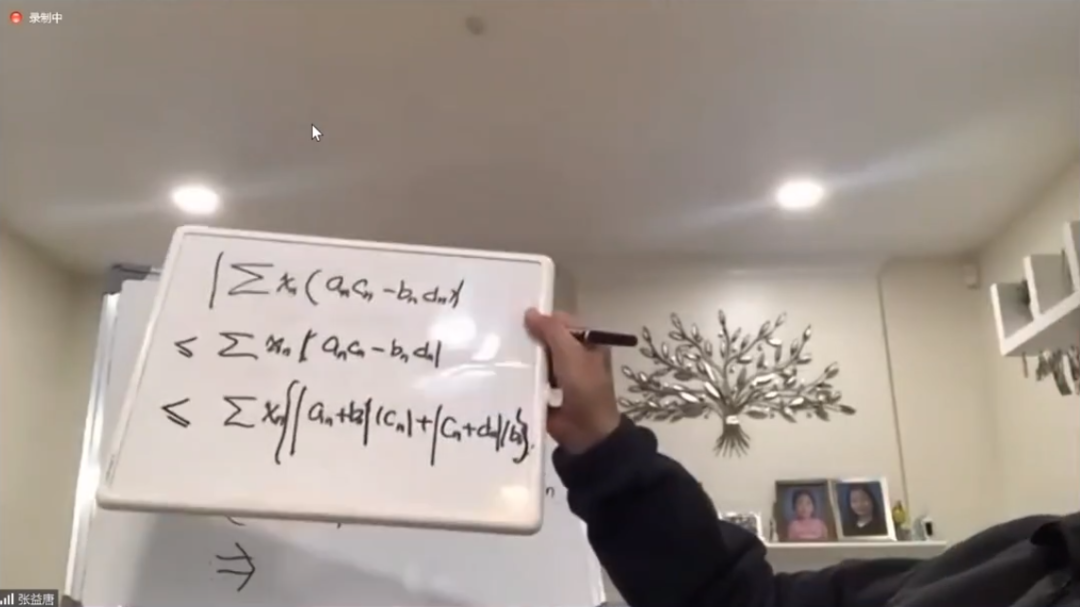
我们有这样一个关系式,但是我们可以证明,实际上可以假定χn是非负的,我们可以用柯西不等式来估计下面这个的上界。
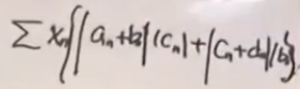
最后我们发现我们得到一个矛盾(算这个和不如用柯西不等式),我们发现算这个东西是不对的,左边应该是比右边的更大,于是用这个方式就推出矛盾来了。
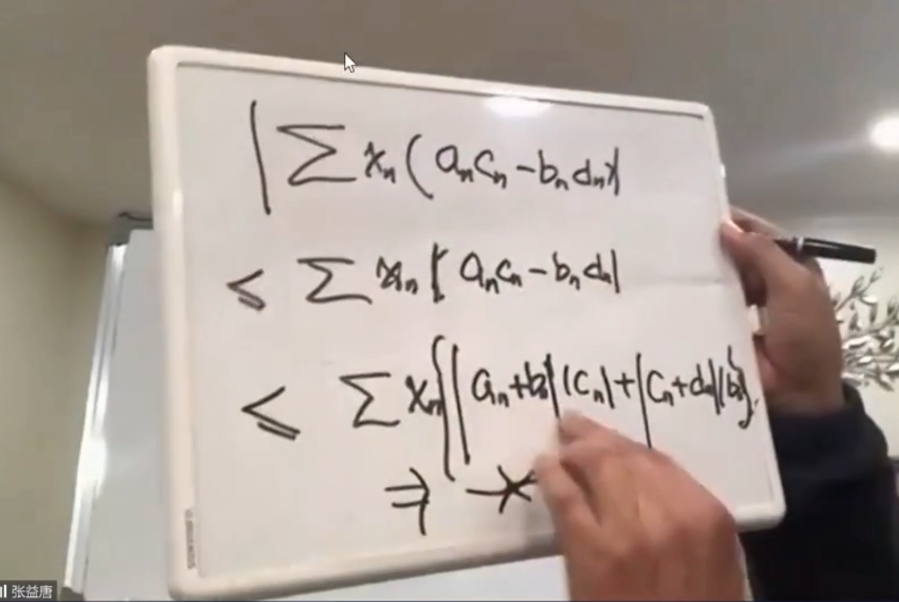
大家有兴趣的话可以翻译一下我这篇文章,在第二节最后,我是用三个proposition就把它给弄下来了,然后剩下的就是去证明那三个proposition。
我们考虑一下数论的历史,一开始我们总是有这样的问题,要去构造一个yn。第一个条件是,这个yn必须是非负的,或者什么样,然后它乘以χn,加起来要小于0,要去构造这样一个yn。
最早是Brown在1718年 ,用默比乌斯函数的组合来构造出这样一个东西。
后来自从Selburg之后,yn就取成zn的平方,这个东西一直沿用下来。
当时我在做孪生素数猜想,我们也知道,yn等于zn平方,它只是一个能够保证它大于等于0的充分条件,但不是必要条件,还有没有别的形式 ?
有很多人想过,但目前为止没有人想出来(yn不是这个平方的形式)。
在我在这里,似乎有一种新的办法(更复杂),实际上我是引进了4个序列。
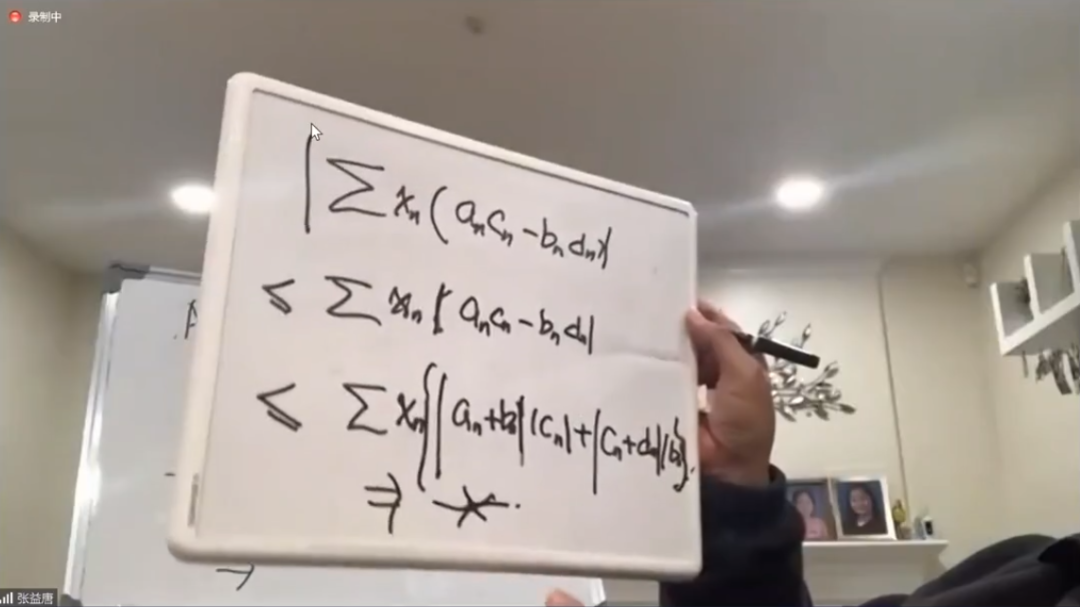
最后如果这些χn都是大于0,我能推出矛盾来。
今天我就先讲到这儿,这个东西作为介绍性的,我也只能讲得比较初等一点。
PS:如有错误,欢迎在留言中指正。
论文浅析
在这篇最新的论文中,张益唐教授提出了两个定理。
第一,对于L(1,χ)的估计:

第二,可能存在的西格尔零点不大于:
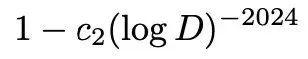
其中,c1和c2都是正实数,且与D无关。

论文地址:https://arxiv.org/abs/2211.02515
此前,张益唐教授证明朗道-西格尔零点猜想的论文已经广泛流传,由于全篇涉及解析数论等硬核知识,对于广大网友的理解门槛还是相当高的。
论文公布之后,来自知乎、B站、微博等媒体平台的各路专业人士和UP主的解读也为数不少了。
比如B站知识区UP「钰子一」对这篇论文结论的初步解读:
他的看法是,在假定张益唐教授的证明是正确的情况下(因为论文目前尚未经同行评议),这篇论文确实是距离证明真正的「零点猜想」最近的一次突破性成果。
下面是真正的「朗道-西格尔零点猜想」:

注意非零域的范围,最后一项的指数为-1。
张益唐教授这次在论文中成功证明的定理1和定理2,其中2是1的推论:


可以看到,定理2的最后一项的指数为-2024,而原始的「零点猜想」的指数为-1。
换句话说,这是目前关于朗道-西格尔零点猜想问题上,已证结论和待证的「终极目标」之间,距离最近的一次。
张益唐教授在文末表示,这个-2024的指数值,可以取得更大一些,但目前按照论文中的思路,可能取不到-1。
除了热心网友的粗浅解析,来自山东大学的解析数论专家在「张益唐教授谈朗道-西格尔零点猜想研究的新突破」中,也对张益唐教授这次的工作进行了专业角度的解析。
由于全体模D的狄利克雷特征(Dirichlet character)的适当线性组合,可以表示出模D算术级数的计数函数。因此,狄利克雷L-函数(Dirichlet L-series)与算术级数中的素数分布问题密切相关。
对于固定的狄利克雷特征,黎曼ζ函数的解析性质大多容易推广到相应的狄利克雷L-函数上去。比如当特征是复特征时,其L-函数与黎曼ζ函数有类似的非零区域:
![]()
但是,当特征是实原特征时,在区间
![]()
内至多可能存在一个一阶实零点,这里c是一个适当的正常数。
张益唐教授在最新预印本论文里证明了,模D的实原特征L-函数在区间
![]()
内没有实零点,这里c是绝对实效正常数。如果把这里的2024换成1,就得到原始形式的朗道-西格尔零点猜想。
专家指出,2024虽然大于1,但在数学意义上,与1并没有实质性的差别。
朗道-西格尔零点猜想
1859年,德国数学家黎曼在论文「论小于给定数值的素数个数」中,首次提及这个猜想。
黎曼发现,质数的分布跟某个函数有着密切关系:
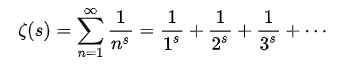
这个公式中,s是复数,可以写成s=a+bi这样的形式(a是s的实部、b是s的虚部、i则是根号负一)。
当s的实部小于1时,整个级数和可能会发散。为了让函数适用于更广的范围,黎曼把上面的ζ函数改写为:
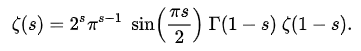
当s为负偶数(s= -2, -4, -6…)时,黎曼ζ函数为零。这些s的值,就称为平凡零点。
不过,此外还有另一些s的值,能够让黎曼ζ函数为零,它们被称为非平凡零点。就是这些非平凡零点,对质数的分布有着决定性影响。
到了这里,黎曼本人也无法证明了。
不过他做了一个猜测:黎曼ζ函数所有非平凡零点的实部都是1/2,或者说黎曼ζ函数在1/2<x<1这一区域内没有零点。这就是黎曼猜想。
随后的数学家们,在前人的基础上继续前进。
为此,数学家狄利克雷引入了狄利克雷L函数。
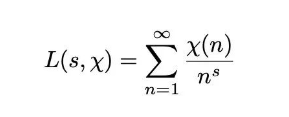
对于这个函数,也有一个猜想:狄利克雷L函数在1/2<x<1这一区域内没有零点。这就是广义黎曼猜想。
倪忆在文章「千呼万唤始出来,张益唐公布证明朗道-西格尔零点猜想的论文」中解释道,如果χ(n)的取值都是实数,那么L(s,χ)在
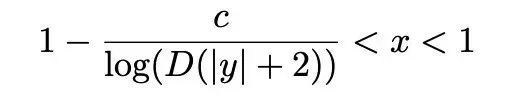
里最多只有一个零点,而且这个零点一定是实数。这个可能存在的零点被称为西格尔零点。而朗道-西格尔零点猜想则断言,西格尔零点是不存在的。
更确切地说,存在一个正实数c,使得对于任何D和相应的实特征χ,L(x,χ)在
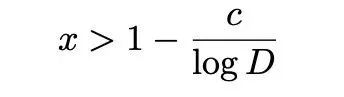
时都不等于0.
倪忆表示,朗道-西格尔零点猜想是广义黎曼假设的一种特殊情形,但这是一种非常重要也非常困难的情形。在很多解析数论问题的研究中,都需要把西格尔零点单独拿出来考虑。
所以一旦证明了朗道-西格尔零点猜想,就可以取得很多新突破,简化和加强很多经典数论结果。
特别鸣谢:
普林小虎队「千呼万唤始出来,张益唐公布证明朗道-西格尔零点猜想的论文」
https://mp.weixin.qq.com/s/OgOsgp2wklSw86LQSnpuAA
山东大学「张益唐教授谈朗道-西格尔零点猜想研究的新突破」
https://mp.weixin.qq.com/s/AuRZOk_yx_dJC2pys9bUMg
钰子一科普张益唐关于朗道-西格尔零点猜想的文章!「他取得了突破性的进展,结论十分漂亮!」
https://www.bilibili.com/video/BV1y24y1f7Tg/?vd_source=eecf800392d116d832e90ad1c9ae70f6
直播录制:
https://www.bilibili.com/video/BV1oP411F7a5/?vd_source=eecf800392d116d832e90ad1c9ae70f6
END
分享
收藏
点赞
在看





















 400
400











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








