四个子空间
行向量的秩是r，列向量的秩是r，
d
i
m
(
n
u
l
l
(
A
)
)
=
r
dim(null(A)) = r
dim(null(A))=r，
d
i
m
(
n
u
l
l
(
A
T
)
)
=
m
−
r
dim(null(A^T) )= m - r
dim(null(AT))=m−r
而且 前两个正交，后两个相交
正交
意思就是向量夹角90°
如果判断?
使用点乘
如果
X
T
∗
y
=
0
X^T*y = 0
XT∗y=0，那么就说他们正交
毕达哥拉斯（勾股定理）
一个边长（向量）的平方，比如说向量 A = [ 1 , 2 , 3 ] T A = [1,2,3]^T A=[1,2,3]T，它的边长的平方就是： X T ∗ X X^T*X XT∗X （其实也就是举例零向量的距离。
举例
更一般化的定理
注意，最后两个是相同的 X T y 和 y T X X^Ty和y^TX XTy和yTX是一摸一样的，所以，就退出了， x T y = 0 x^T y = 0 xTy=0
这就是从毕达哥拉斯同理推出的正交条件。
两个正交向量的点乘为零
零向量与任何向量都相交
正交子空间
定义
子空间S和子空间T正交意味着，所有S中的向量都和T中的向量相交
如果两个子空间在某条直线相遇，那么它肯定不是相交的
行向量正交于 零空间
A
x
=
0
Ax = 0
Ax=0
这样一看就非常明显了
注意：这里的维度非常重要，它们的秩加起来要得零
也就是补集的概念
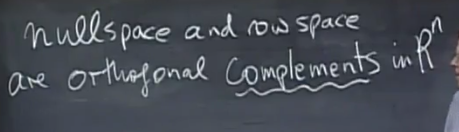
NullSpace包含了所有垂直于行向量的向量
无解方程怎么解？
最最最最重要的的矩阵 A T A A^TA ATA
性质
- 方阵
- 对称
求解方法
把
A
x
=
b
Ax = b
Ax=b
变成
A
T
A
x
=
A
T
b
A^TAx = A^Tb
ATAx=ATb
A T A A^TA ATA可逆的充要条件，是A的列向量互相独立
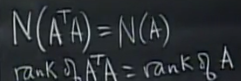
这个公式为什么，下节课再说！
1138
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
