滑动模式观测器（Sliding mode observer）

滑动模式观测器（Sliding mode observer）

Sliding Mode Observer（SMO）是一种基于滑动模式控制理论的状态观测方法，常用于估算系统中的难以直接测量的状态变量，比如电机控制中的转子位置或速度。SMO 具有对模型参数扰动和外部扰动的强鲁棒性，因此在电机控制系统中尤其受到青睐。
滑动模式控制属于非线性控制，滑动模式观测器会有非线性高增益观测器的特性，可以在有限时间内将观测器的误差收敛到零。此外，切换模式的观测器类似卡尔曼滤波，可以允许一些程度的量测噪声。

SMC部分理论

滑动模式控制（sliding mode control, SMC)，是一种非线性控制的技术，利用不连续的控制信号来调整非线性系统的特性，强迫系统在二个系统的正常状态之间滑动，最后进入稳态。SMC状态-反馈控制律不是时间的连续函数,控制律会依目前在状态空间中的位置不同，可能从一个连续的控制系统切换到另一个连续的控制系统。
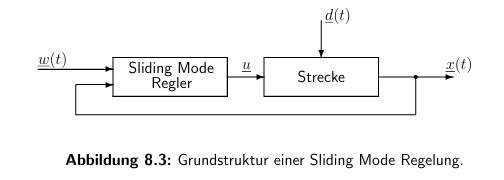
下文将讨论带有开关控制器的控制系统。它们是混合系统的一种特例，可以用右侧不连续的微分方程来描述。滑动模式控制的目的是在控制变量之间来回切换，这样，假设切换频率无限高，系统状态就会沿着状态空间中的切换流形（滑动模式）发生滑动运动。这种设计方法的特点是对参数波动和外部干扰具有鲁棒性。此外，它还能减少阶次，从而为复杂非线性系统的控制设计提供了一种有效的方法.

以下是具有加性扰动的 n 维系统:

未知函数 d(x,t)表示系统的不确定性的外部干扰。系统的操纵变量由系统状态的不连续函数决定。


其中，s(x) 是系统状态的函数。
加粗样式
滑动模式的存在是通过分析接近阶段来确定的。至少对于切换面 S 的子集 D，其轨迹必须从两侧指向切换面 S。从两侧向切换面移动。D 称为滑动模式域。形式上，D 的定义是
所有 x ∈ S，且：

满足这个条件，滑动模式控制才可能存在。选择合适的滑动开关函数S(x)即可。

SMO 基本原理（PMSM）

滑模观测器（SMO）属于一类非线性观测器，用于根据测量的输入和输出估计可观测系统的内部状态。在PMSM中，SMO 用于估计 PMSM 的反向 EMF。 与传统的基于线性反向电磁场的转子位置和速度估计相比，使用 SMO 的主要优势在于其在存在未知信号和不确定性时的鲁棒性。 滑动模式观测器模块通过使用沿αβ 参考坐标系下的 α 轴和 β 轴的电压和电流值来计算 PMSM 的电气位置和机械速度。

估算 BEMF

SMO 利用 PMSM 系统模型、电压和电流矢量输入估算 BEMF。下图显示了基于 SMO 的转子位置和速度估算方法的简化框图。

以下方程组表示 PMSM 电机的状态空间模型：

观察器可以表达如下：

σ是滑动函数，L 是反电磁场观测器极点布置矩阵。
根据以上公式，估计误差可表示如下：

滑动函数 σ 被设计为估计误差的不连续函数，以确保滑动条件，并在有限时间内将系统状态强制为零。比如采用以下滑模函数：

如果滑动模态函数中的 m 值足够大，就能达到滑动条件，因此误差动态变化为零。这意味着：

因此，根据这些方程，反电动势观测器的误差动态可表示为：
对于稳定的反电动势观测器而言，矩阵部分应具有负特征值。换句话说，对于 λ 的特征值，矩阵 L 可按如下方式确定：

转子角度计算

根据观测到的反向电动势，利用以下关系计算出转子位置：

转子转速计算

转子速度可通过观测到的转子位置值计算得出。转子位置角的增量变化用于计算移动平均滤波器中的速度。

计算出的转子速度通过一个截止频率为 Θc 的低通滤波器 (LPF) 进一步滤波，以避免不必要的干扰影响结果。LPF 可以离散时间方式实现，采样时间 Ts 如下：

SMO总结：

特性	描述
基本原理	使用滑模控制思想逼近真实状态
核心组件	状态空间模型 + sign函数
优点	鲁棒性强、估计速度快、适合无传感器控制
缺点	易产生抖振，需滤波或光滑处理
应用	无传感器控制、状态反馈、故障诊断等