无感FOC之滑膜观测器

目录

一，简述

二，SMO基本原理

三，基本步骤

1. 建立电机的数学模型

2. 设计滑模观测器

3. 估计反电动势

4. 滑模增益的选择

5. 实现滑模观测器

 6.滑膜观测器运行过程

四，代码实例

五，代码解释

六，电机位置及速度计算

1，永磁同步电机

2，直流无刷电机

注意事项

---

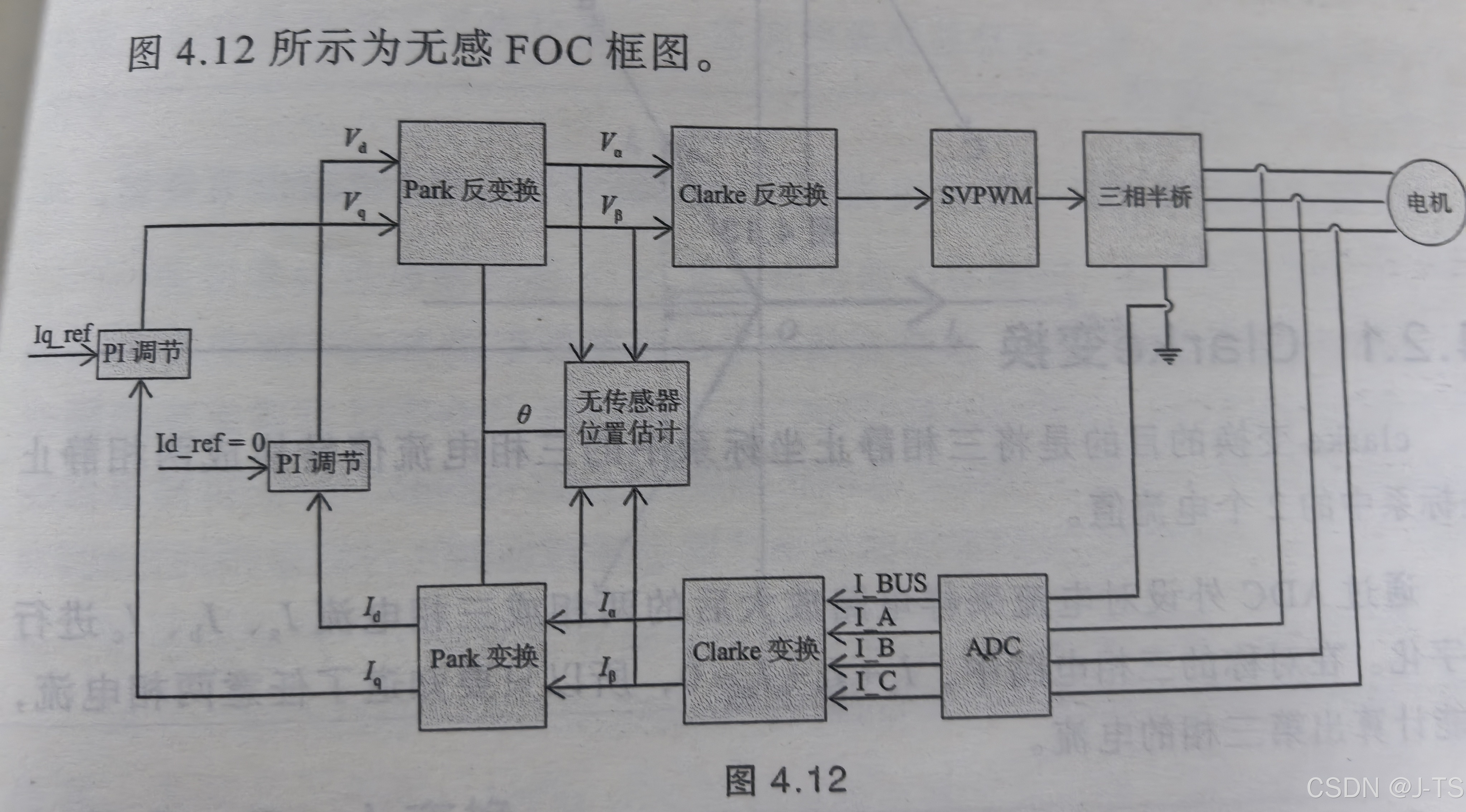
一，简述

无感FOC相对于有感就是没有了编码器来获取位置和速度，那么我们就需要一个观测器来获取一些信息，从而计算出电机的角度和速度。这里我们使用滑膜观测器。滑模观测器（Sliding Mode Observer，SMO）是一种用于估计系统状态的有效方法，在电机控制中，可用于观测电机的反电动势。下面将以永磁同步电机（PMSM）为例，详细介绍利用滑模观测器观测电机反电动势的步骤和原理。

FOC算法及SVPWM我们之前已经讲过：FOC算法（SVPWM算法）_definition of crossing point-CSDN博客

新整理的文章：FOC算法与SVPWM-CSDN博客

二，SMO基本原理

滑模观测器的核心思想是通过设计一个滑模面，使得观测器的状态误差能够在有限时间内收敛到滑模面上，并在滑模面上保持滑动，从而实现对系统状态的准确估计。对于电机的反电动势观测，滑模观测器通过比较电机的实际电流和观测电流，产生一个误差信号，然后利用滑模控制律来调整观测器的参数，使得误差信号收敛到零，进而得到准确的反电动势估计值。

三，基本步骤

1. 建立电机的数学模型

以永磁同步电机在两相静止坐标系（α - β 坐标系）下的电压方程为例：

其中，u_alpha、u_beta 是 α - β 坐标系下的定子电压分量；i_alpha、i_beta 是 α - β 坐标系下的定子电流分量；R 是定子电阻；L 是定子电感；e_alpha、e_beta 是 α - β 坐标系下的反电动势分量。

2. 设计滑模观测器

根据电机的数学模型，设计滑模观测器的方程：

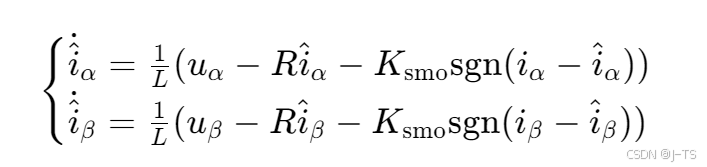
其中，hat{i}_alpha、hat{i}_beta 是观测电流；K_{smo}是滑模增益；{sgn}是符号函数，定义为：

3. 估计反电动势

通过滑模观测器得到观测电流后，可以进一步估计反电动势：

其中，hat{e}_alpha、hat{e}_beta 是估计的反电动势。

4. 滑模增益的选择

滑模增益 K_smo的选择对滑模观测器的性能有重要影响。增益过大可能会导致系统出现抖振现象，增益过小则可能导致观测误差增大。一般可以通过实验或理论分析来选择合适的滑模增益。

5. 实现滑模观测器

在实际应用中，可以使用数字信号处理器（DSP）或现场可编程门阵列（FPGA）来实现滑模观测器。具体步骤如下：

• 采样电机电流和电压：使用电流传感器和电压传感器采集电机的定子电流和电压信号。
• 离散化滑模观测器方程：将连续时间的滑模观测器方程离散化，以便在数字系统中实现。常用的离散化方法有欧拉法、梯形法等。
• 编写程序代码：根据离散化后的滑模观测器方程，编写相应的程序代码，实现反电动势的实时估计。

 6.滑膜观测器运行过程

7.SMO建模分析

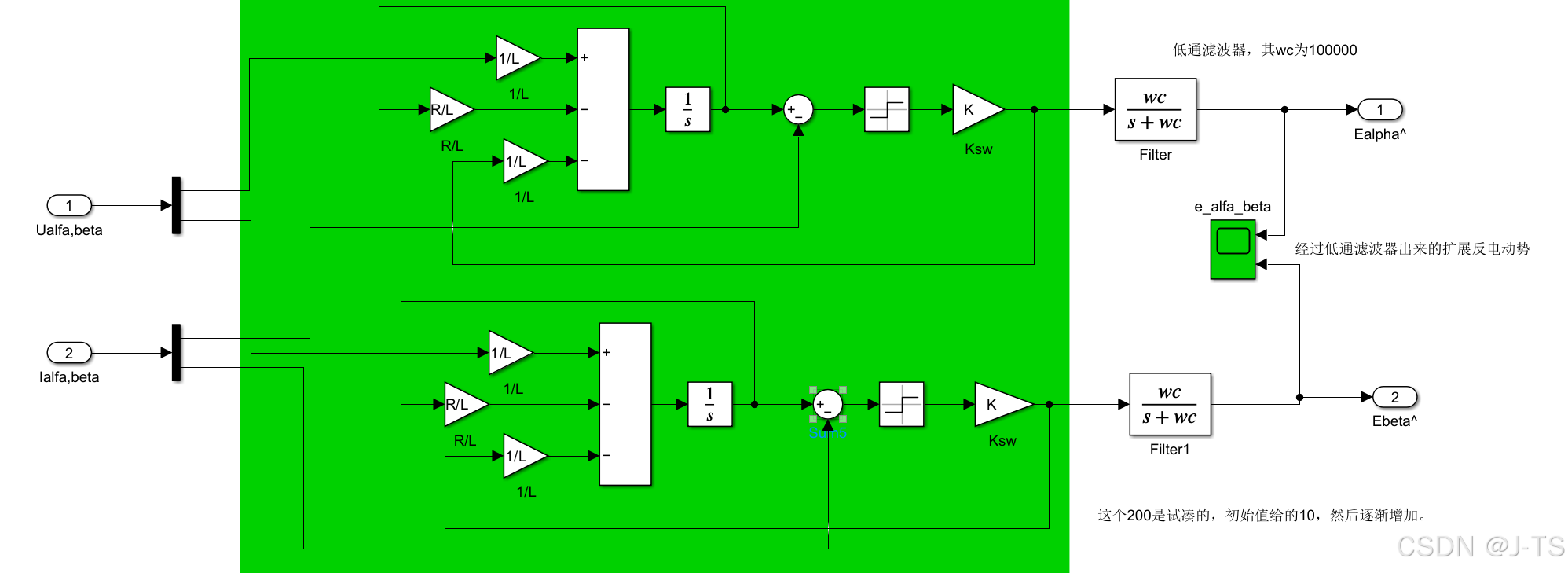
在中我们可以看到滑膜观测的的建模完全符合前面推导的公式，积分出来的对应hat_i_alpha/beta，从K（增益模块）后面出来对应公式里的最后一项，然后将这些值放到前面的加减法运算模块中（将公式的1/L乘到括号里面），只有u_alpha/L那一项为正，其余做减法运算，整个流程完全符合公式。

四，代码实例

/* 符号函数近似 - 使用饱和函数代替 */
static float sign(float x) {
    if (x > SMO_BOUNDARY_LAYER) return 1.0f;
    if (x < -SMO_BOUNDARY_LAYER) return -1.0f;
    return x / SMO_BOUNDARY_LAYER;
}
 
/* 初始化滑模观测器 */
void SMO_Init(SMO_TypeDef *smo) {
    smo->i_alpha = 0.0f;
    smo->i_beta = 0.0f;
    smo->v_alpha = 0.0f;
    smo->v_beta = 0.0f;
    smo->e_alpha = 0.0f;
    smo->e_beta = 0.0f;
    smo->z_alpha = 0.0f;
    smo->z_beta = 0.0f;
    smo->theta_est = 0.0f;
    smo->speed_est = 0.0f;
    smo->speed_est_rpm = 0.0f;
    smo->speed_lpf = 0.0f;
}
 
/* 更新滑模观测器 */
void SMO_Update(SMO_TypeDef *smo, float i_alpha, float i_beta, float v_alpha, float v_beta, float dt) {
    float err_alpha, err_beta;
    float e_alpha_prev, e_beta_prev;
    
    // 保存当前反电动势值 
    e_alpha_prev = smo->e_alpha;
    e_beta_prev = smo->e_beta;
    
    // 更新电流和电压值 
    smo->i_alpha = i_alpha;
    smo->i_beta = i_beta;
    smo->v_alpha = v_alpha;
    smo->v_beta = v_beta;
    
    // 计算电流误差 
    err_alpha = smo->i_alpha - smo->z_alpha;
    err_beta = smo->i_beta - smo->z_beta;
    
    // 更新滑模变量 
    smo->z_alpha += dt * ((1.0f/LS) * (smo->v_alpha - RS * smo->i_alpha) + (SMO_K_SLIDE/LS) * sign(err_alpha));
    smo->z_beta += dt * ((1.0f/LS) * (smo->v_beta - RS * smo->i_beta) + (SMO_K_SLIDE/LS) * sign(err_beta));
    
    // 估算反电动势 (低通滤波)
    smo->e_alpha = SMO_K_SLIDE * sign(err_alpha);
    smo->e_beta = SMO_K_SLIDE * sign(err_beta);
    
    // 一阶低通滤波反电动势 
    float lpf_coeff = 2.0f * PI * SMO_FILTER_CUTOFF * dt;
    lpf_coeff = (lpf_coeff > 1.0f) ? 1.0f : lpf_coeff;
    smo->e_alpha = e_alpha_prev + lpf_coeff * (smo->e_alpha - e_alpha_prev);
    smo->e_beta = e_beta_prev + lpf_coeff * (smo->e_beta - e_beta_prev);
    
    // 估算电角度 
    smo->theta_est = atan2f(-smo->e_alpha, smo->e_beta);
    
    // 确保角度在0-2π范围内 
    if (smo->theta_est < 0) {
        smo->theta_est += 2.0f * PI;
    }
    
    // 估算电速度 (通过反电动势幅值和角度差分)
    float e_magnitude = sqrtf(smo->e_alpha * smo->e_alpha + smo->e_beta * smo->e_beta);
    smo->speed_est = e_magnitude / FLUX_LINKAGE;
    
    // 角度差分速度估算 
    static float theta_prev = 0.0f;
    float delta_theta = smo->theta_est - theta_prev;
    
    // 处理角度环绕 
    if (delta_theta > PI) delta_theta -= 2.0f * PI;
    if (delta_theta < -PI) delta_theta += 2.0f * PI;
    
    float speed_diff = delta_theta / dt;
    theta_prev = smo->theta_est;
    
    // 结合两种速度估算方法 
    smo->speed_est = 0.7f * smo->speed_est + 0.3f * speed_diff;
    
    // 低通滤波速度 
    smo->speed_lpf = smo->speed_lpf + SPEED_EST_ALPHA * (smo->speed_est - smo->speed_lpf);
    
    // 转换为机械转速 (RPM)
    smo->speed_est_rpm = (smo->speed_lpf * 60.0f) / (2.0f * PI * POLE_PAIRS);
}
 
/* 获取估算的电角度 */
float SMO_GetElectricalAngle(SMO_TypeDef *smo) {
    return smo->theta_est;
}
 
/* 获取估算的电速度 (rad/s) */
float SMO_GetSpeedEstimate(SMO_TypeDef *smo) {
    return smo->speed_lpf;
}
 
/* 获取估算的机械转速 (RPM) */
float SMO_GetSpeedEstimateRPM(SMO_TypeDef *smo) {
    return smo->speed_est_rpm;
}

#ifndef _SMO_H_
#define _SMO_H_
/***********************************头文件区**************************************/
#include "foc.h"
/***********************************外部变量**************************************/


/**********************************宏定义****************************************/
/* 电机参数宏定义 - 需要根据实际电机修改 */
#define POLE_PAIRS         7       // 电机极对数 
#define RS                 0.194f    // 定子电阻(欧姆)
#define LS                 0.097e-3f  // 定子电感(H)
#define FLUX_LINKAGE       0.028571f   // 永磁体磁链(Wb)
#define J                  0.0001f // 转动惯量(kg.m^2)
#define B                  0.0001f // 阻尼系数 
 
/* SMO参数 */
#define SMO_K_SLIDE        50.0f   // 滑模增益 
#define SMO_BOUNDARY_LAYER 0.1f    // 边界层厚度 
#define SMO_FILTER_CUTOFF  1000.0f // 低通滤波器截止频率(Hz)
 
/* 电流采样相关 */
#define CURRENT_GAIN       0.001f  // 电流采样增益(A/count)
#define VDC                24.0f   // 直流母线电压(V)
#define PWM_MAX            8400    // PWM最大值(对应100%占空比)
 
/* 速度估算参数 */
#define SPEED_EST_CUTOFF   500.0f   // 速度估算低通截止频率(Hz)
#define SPEED_EST_ALPHA    0.1f    // 速度估算滤波器系数 

/********************************结构体**********************************************/ 
/* 结构体定义 */
typedef struct {
    float i_alpha;          // α轴电流 
    float i_beta;           // β轴电流 
    float v_alpha;          // α轴电压 
    float v_beta;           // β轴电压 
    float e_alpha;          // α轴反电动势 
    float e_beta;           // β轴反电动势 
    float z_alpha;          // α轴滑模变量 
    float z_beta;           // β轴滑模变量 
    float theta_est;        // 估算的电角度(rad)
    float speed_est;        // 估算的电速度(rad/s)
    float speed_est_rpm;    // 估算的机械转速(RPM)
    float speed_lpf;        // 低通滤波后的速度 
} SMO_TypeDef;

/********************************外部变量*****************************************/
extern SMO_TypeDef SMO;

/***********************************函数声明**************************************/


void SMO_Init(SMO_TypeDef *smo);
void SMO_Update(SMO_TypeDef *smo, float i_alpha, float i_beta, float v_alpha, float v_beta, float dt);
float SMO_GetElectricalAngle(SMO_TypeDef *smo);
float SMO_GetSpeedEstimate(SMO_TypeDef *smo);
float SMO_GetSpeedEstimateRPM(SMO_TypeDef *smo);

#endif

五，电机位置及速度计算

1，永磁同步电机

# 假设已知相邻两个时刻的电角度
theta_e_k = 0.5
theta_e_k_1 = 0.3
T_s = 0.01

omega_e = (theta_e_k - theta_e_k_1) / T_s
print(f"电机电角速度: {omega_e} 弧度/秒")

建模分析

注：蓝色部分为低通滤波的补偿

注意事项

• 滤波处理：实际测量的反电动势信号中可能包含噪声，需要进行滤波处理，以提高位置和速度计算的准确性。
• 参数校准：电机的永磁体磁链等参数可能会随着温度、老化等因素发生变化，需要进行定期校准。
• 初始位置估计：在电机启动时，需要采用特殊的方法来估计电机的初始位置，以确保电机能够正常启动。

现在我们就可以利用滑膜观测器估算出电机的位置和速度了。后续会更新如何在MATLAB中建模，请持续关注。

无感

有感

​​​​​​​

六，无感FOC启动算法

无感FOC启动算法有很多，作者建议初学者先使用简单可靠的普通启动算法，如三段式启动算法。

1，需要启动算法的原因

无感磁场定向控制（FOC）是一种先进的电机控制技术，它通过估计电机转子的位置和速度来实现精确的电机控制。然而，在电机静止或低速运行时，由于反电动势信号非常微弱甚至为零，传统的基于反电动势的转子位置估算方法无法准确工作，导致无法确定转子的初始位置，从而无法正确地施加定子电压矢量来驱动电机启动。因此，需要专门的启动算法来帮助电机从静止状态平稳地过渡到能够正常使用反电动势法进行位置估算的运行状态。

2，三段式启动

原理

三段式启动算法主要分为三个阶段：转子预定位、速度开环加速和闭环切换。

1. 转子预定位：给电机施加一个固定的电压矢量，使转子旋转到一个已知的初始位置。这个阶段的目的是消除转子初始位置的不确定性。
2. 速度开环加速：以一个预先设定的加速度逐渐增加电机的转速，在这个阶段，电机的控制是基于开环速度控制，不依赖于转子位置的反馈。
3. 闭环切换：当电机的转速达到一定值，反电动势信号足够强时，切换到基于反电动势的无感 FOC 闭环控制。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>

// 定义电机控制参数
#define PRE_POSITIONING_TIME 2000  // 转子预定位时间，单位：ms
#define OPEN_LOOP_ACCELERATION 5    // 开环加速阶段的加速度，单位：rpm/s
#define SWITCHING_SPEED 1000       // 切换到闭环控制的速度阈值，单位：rpm
#define CONTROL_PERIOD 10          // 控制周期，单位：ms

// 全局变量
int currentSpeed = 0;  // 当前电机速度，单位：rpm
int elapsedTime = 0;   // 经过的时间，单位：ms

// 模拟电机控制函数
void applyVoltageVector(double angle, double magnitude) {
    // 这里应该是实际的硬件操作，用于向电机施加电压矢量
    // 为了简化，这里只是打印信息
    printf("Applying voltage vector: Angle = %.2f degrees, Magnitude = %.2f\n", angle, magnitude);
}

// 转子预定位函数
void prePositioning() {
    printf("Starting pre - positioning...\n");
    double prePositioningAngle = 0;  // 固定的预定位角度
    double prePositioningMagnitude = 10.0;  // 固定的预定位电压幅值

    // 施加固定电压矢量，使转子旋转到初始位置
    for (int i = 0; i < PRE_POSITIONING_TIME / CONTROL_PERIOD; i++) {
        applyVoltageVector(prePositioningAngle, prePositioningMagnitude);
        elapsedTime += CONTROL_PERIOD;
        // 模拟延时
        for (volatile int j = 0; j < 100000; j++); 
    }
    printf("Pre - positioning completed.\n");
}

// 速度开环加速函数
void openLoopAcceleration() {
    printf("Starting open - loop acceleration...\n");
    while (currentSpeed < SWITCHING_SPEED) {
        // 增加速度
        currentSpeed += OPEN_LOOP_ACCELERATION * CONTROL_PERIOD / 1000;

        // 根据当前速度计算电压矢量的角度和幅值
        double angle = (double)currentSpeed * 360 / 60 * elapsedTime / 1000;  // 简单的角度计算
        double magnitude = 10.0 + (double)currentSpeed / SWITCHING_SPEED * 10.0;  // 幅值随速度增加

        // 施加电压矢量
        applyVoltageVector(angle, magnitude);

        elapsedTime += CONTROL_PERIOD;
        // 模拟延时
        for (volatile int j = 0; j < 100000; j++); 
    }
    printf("Open - loop acceleration completed. Current speed: %d rpm\n", currentSpeed);
}

// 闭环控制函数（简化示例）
void closeLoopControl() {
    printf("Switching to closed - loop control...\n");
    while (1) {
        // 这里应该是读取反电动势信号，估算转子位置和速度
        // 为了简化，假设已经有了估算的速度和位置
        int estimatedSpeed = currentSpeed;  // 模拟估算速度
        double estimatedAngle = (double)estimatedSpeed * 360 / 60 * elapsedTime / 1000;  // 模拟估算角度

        // 根据估算结果调整电压矢量
        double magnitude = 20.0;  // 固定幅值
        applyVoltageVector(estimatedAngle, magnitude);

        elapsedTime += CONTROL_PERIOD;
        // 模拟延时
        for (volatile int j = 0; j < 100000; j++); 
    }
}

// 主函数
int main() {
    // 阶段1：转子预定位
    prePositioning();

    // 阶段2：速度开环加速
    openLoopAcceleration();

    // 阶段3：闭环切换
    closeLoopControl();

    return 0;
}

代码说明：

1. 参数定义：

   • PRE_POSITIONING_TIME：转子预定位所需的时间，单位为毫秒。
   • OPEN_LOOP_ACCELERATION：开环加速阶段的加速度，单位为每分钟转数每秒（rpm/s）。
   • SWITCHING_SPEED：切换到闭环控制的速度阈值，单位为 rpm。
   • CONTROL_PERIOD：控制周期，单位为毫秒。

2. 全局变量：

   • currentSpeed：当前电机的速度，单位为 rpm。
   • elapsedTime：从启动开始经过的时间，单位为毫秒。

3. applyVoltageVector 函数：

   • 该函数用于模拟向电机施加电压矢量的操作。在实际应用中，这里应该是与硬件交互的代码，例如通过 PWM 输出控制电机。

4. prePositioning 函数：

   • 实现转子预定位阶段，通过在一段时间内施加固定的电压矢量，使转子旋转到初始位置。

5. openLoopAcceleration 函数：

   • 实现速度开环加速阶段，根据设定的加速度逐渐增加电机速度，并根据当前速度计算电压矢量的角度和幅值，然后施加到电机上。

6. closeLoopControl 函数：

   • 实现闭环控制阶段，模拟读取反电动势信号估算转子位置和速度，并根据估算结果调整电压矢量。

7. main 函数：

   • 依次调用三个阶段的函数，完成电机的启动过程。

注意事项：

• 此代码中的延时部分使用了 for 循环进行简单模拟，实际应用中应该使用硬件定时器来实现精确的延时。
• applyVoltageVector 函数只是一个模拟函数，需要根据具体的硬件平台进行替换。
• 闭环控制阶段的转子位置和速度估算部分是简化模拟，实际应用中需要使用反电动势检测和相关算法来实现。
• 在使用无感算法之前一定要先验证ADC电流采样正确无误。（可用开环代码验证，注意将角度累加且限制到2*PI内）

• 	static float theta;
  	theta += 0.01f;
  	if(theta >= 2*PI)		theta -= 2*PI;
  	else if(theta <= 0)	theta += 2*PI;